84. Что называют магнитным доменом?

Домен – область спонтанной намагниченности в ферромагнитном кристалле.

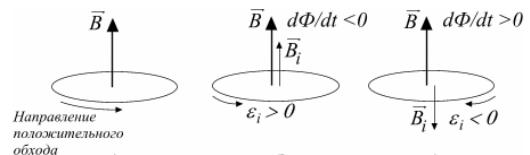
86. В чем состоит правило Ленца? Поясните ответ рисунками. (стр. 66)

Правило Ленца определяет направление индукционного тока и гласит: Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

88. В чем состоит гипотеза Максвелла? (стр. 68)

Максвелл предположил, что появление ЭДС индукции в неподвижном контуром вызвано вихревым электрическим полем, порождаемое переменным магнитным полем.

90. Поясните физический смысл индуктивности проводника применительно к замкнутому контуру. (стр. 69)

Индуктивность контура показывает, какой магнитный поток пронизывает контур при силе тока в нём равном 1 А. Единица измерения индуктивности: [L]=Гн (генри).

92. Напишите дифференциальное уравнение и закон изменения силы тока при замыкании электрической цепи. (стр. 71)

Любое изменение тока в цепи порождает появление в ней ЭДС самоиндукции.

94. Напишите формулы для энергии магнитного поля. На каком основании можно утверждать, что магнитное поле обладает энергией? (стр. 72)

.

Опыт с лампочкой доказывает о существовании энергии магнитного поля, т.к. после отключения источника питания некоторое время лампочка продолжает гореть.

96. Какое из уравнений Максвелла отражает тот факт, что источником электрического поля являются электрические заряды? (стр. 75)

Согласно уравнениям Максвелла (первое и третье), источниками электрического поля могут быть либо непосредственно электрические заряды, либо меняющиеся во времени магнитные поля.

98. Что называют током смещения? (стр. 73)

, ток протекает через конденсатор, где dq- заряд, пришедший на обкладку конденсатора за время dt.

100. В чем состоит физический смысл теоремы о циркуляции, входящей в уравнения Максвелла? (стр. 73)

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

^

102. Дать определение частоты колебаний.

Частота колебаний - число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).

Частота колебаний равна одному Герцу, если за 1 секунду совершается 1 полное колебание. 1Гц=1с^-1

104. Что называют пружинным маятником?

Пружинным маятником называют точечную массу, колеблющуюся на пружине вдоль вертикальной или горизонтальной оси.

106. Дайте определение малых колебаний.

Малые колебания - это колебания, при которых ускорение пропорционально координате x : , а период

108. Сформулируйте условия возникновения малых колебаний.

1) Наличие положения устойчивого равновесия;

2) Наличие силы, зависящей от координаты;

3) Наличие в системе избыточной энергии;

4) Достаточно малые силы трения (сопротивления) в системе.

110. Как и от чего зависит возвращающая сила при гармонических колебаниях?

Возвращающая сила со стороны пружины подчиняется закону Гука – линейно зависит от величины ее деформации. m = −kx .

112. Напишите дифференциальное уравнение гармонических колебаний.

, где и -амплитуда колебаний скорости.

114. Как циклическая частота колебаний связана с периодом колебаний?

ω = 2πv = 2π/T

Параметр - называют циклической частотой из-за характерной связи с частотой и периодом колебаний.

116. Напишите закон гармонических колебаний.

Поведение механических систем определяется законами динамики. Запишем второй закон Ньютона для груза массой m, полагая, что возвращающая сила со стороны пружины подчиняется закону Гука – линейно зависит от величины ее деформации

118. Что называют фазой колебаний?

Фаза колебания - - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад).

Фаза колебания в нач. момент времени (t=0) называется начальной фазой .

120. Напишите закон изменения скорости при синусоидальных гармонических колебаниях.

, где и - циклическая частота.

122. Напишите формулу полной энергии колебаний.

Полная энергия колебаний пропорциональна квадрату амплитуды колебаний .

- полная энергия колебательной системы.

- координата.

124. Каковы фазовые соотношения между кинетической и потенциальной энергией колебаний?

126. Как и от его зависит циклическая частота собственных колебаний физического маятника?

- собственная частота колебаний

128. Что принимают в качестве обобщенной координаты для колебательного контура?

В электрическим колебательном контуре в качестве величины характеризующей состояние системы (обобщенной координаты) естественно выбрать заряд конденсатора q .

ψ– обобщенная координата системы. Ее поведение описывается нелинейным дифференциальным уравнением:

130. Напишите дифференциальное уравнение затухающих колебаний.

где - собственная частота колебаний без затухания;

β = γ/ 2m - коэффициент затухания.

132. Напишите условие апериодичности затухающих колебаний.

При большом затухании ( β > ω₀ ) корни λ_1,2 –вещественны. И решением является просто сумма двух экспонент:

Система экспоненциально приближается к состоянию равновесия. Выбор подходящих начальных условий позволяет один раз это состояние проскочить.

134. Что называют характерным временем затухания?

Характерное время затухания (время релаксации) τ =1/β , в течение которого амплитуда колебаний уменьшается в е раз.

136. Что называют логарифмическим декрементом затухания?

Величиной, характеризующей, как быстро спадает амплитуда колебаний, является логарифмический декремент затухания χ , определяемый формулой

138. Что называют добротностью колебательной системы?

Добротность колебательной системы Q. Это величина, пропорциональная числу колебаний N_e = τ/T , которое совершается осциллятором за время релаксации:

Q =πN_e

Чем выше добротность, тем больше колебаний совершает система за характерное время, тем медленнее затухают колебания

140. Напишите дифференциальное уравнение вынужденных колебаний.

142. От чего и как зависит амплитуда вынужденных колебаний?

Амплитуда a установившихся колебаний зависит от соотношения частоты вынуждающей силы ω и собственной частоты колебаний ω₀. Функция a(ω) , описывающая зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы, называется амплитудно-частотной характеристикой.

144. Что называют резонансом?

Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы

146. Дайте определение моды колебаний.

Нормальной модой называют колебание, при котором все движущиеся элементы системы совершают колебания с одной частотой и одновременно проходят положение равновесия.

148. Что представляет собой закон колебаний для системы со многими степенями свободы?

\\для_двух_степеней_свободы

150. Нарисуйте моды колебаний двух связанных математических маятников. (стр. 90)

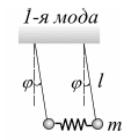
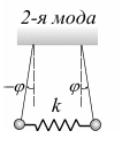Для двух математических маятников длиной l массами m , связанных упругой пружиной жесткостью k , нормальные моды колебаний, очевидно, имеют вид, показанный на рис.

152. Что характерно для биений? (стр. 91)

Биения возникают в результате сложения двух колебаний с близкими частотами.

Биения представляют собой колебания с несущей частотой . Когда амплитуда колебаний одного маятника максимальна, амплитуда другого – минимальна.

, - частота колебаний

- амплитуда обоих колебаний

При закон колебаний имеет вид:

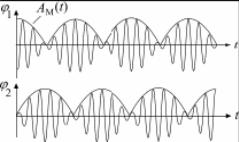
154. Чему равна частота биений?

Частота биений=(Число минимумов амплитуды/Время) равна разности частот составляющих колебаний.

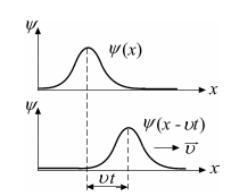
156. Дать определение бегущей волны. (стр. 99)

Бегущей волной называют всякое возмущение состояния вещества или поля, распространяющееся в пространстве с течением времени. Напр. : звуковые волны в газе или жидкости – волны давления; электромагнитные волны – взаимопревращение электрического и магнитного полей.

158. Когда амплитуда волны остается постоянной по мере ее продвижения? (стр. 99)

Амплитуда волны остается постоянной, если волна распространяется в одномерной среде, т.к. важное свойство бегущих волн состоит в том, что они переносят энергию и импульс. Амплитуда не меняется при отсутствии трения.

160. Напишите самый общий вид уравнения бегущей волны.

- одномерное ур-е бегущих волн вдоль x. - ур-е профиля волны в . - закон колебания в точке

162. Как получить уравнение бегущей волны из закона колебаний?

Зная закон колебаний, можно получить уравнение бегущей волны. Следует лишь аргумент заменить на .

164. Как из уравнения бегущей волны получить закон колебаний отдельной точки?

Закон колебаний отдельной точки получается методом подстановки аргумента x. Закон колебаний точки шнура с координатой x=0:

166. Что называют дисперсионным соотношением?

Равенство , определяющее частоту как функцию волнового числа , называют дисперсионным соотношением или законом дисперсии. - длина волны, - период колебаний.

168. В чем состоит физический смысл длины волны? (стр. 101)

- расстояние, проходимое волной за время, равное периоду колебаний .

170. Напишите формулу мощности, переносимой волной вдоль упругого шнура. (стр. 102)

- полная энергия

- линейная плотность шнура

- время

- длина шнура

- частота.

 Карев А. С., Флеров В. Д. , Михайлова А.А., Прахова К. А.