7. УРАВНОВЕШИВАНИЕ И БАЛАНСИРОВКА

ВРАЩАЮЩИХСЯ МАСС.

ВИБРОЗАЩИТА МАШИН

7.1. Цели уравновешивания и балансировки

При движении звеньев с переменными скоростями (с ускорением) возникают силы инерции и их моменты, которые принято называть динамическими нагрузками. Их возникновение приводит к вибрации и шуму, которые устраняются уравновешиванием звеньев при проектировании механизма. Это достигается соответствующим подбором масс и моментов инерции.

Для устранения малой неуравновешенности, возникающей после изготовления звеньев и их монтажа из-за несоблюдения размеров в процессе изготовления, неточности сборки, неоднородности материала, звенья балансируют.

7.2. Условия уравновешенности ротора

Деталь, вращающаяся в опорах, называется ротором. При вращении какой-либо i-й массы m на нее действует сила инерции, которую можно разложить на нормальную и тангенциальную составляющие (рис. 7.1).

Величины этих сил можно вычислить по формулам

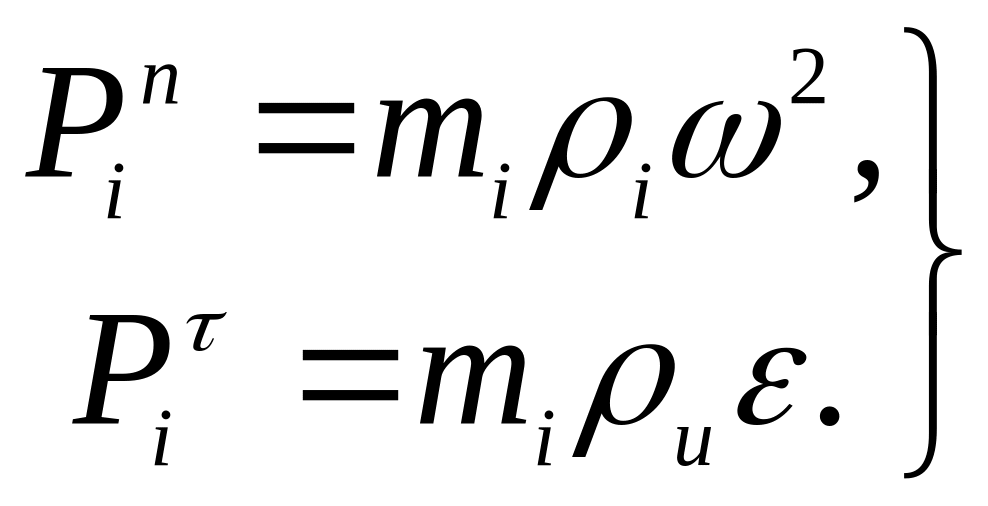(7.1)

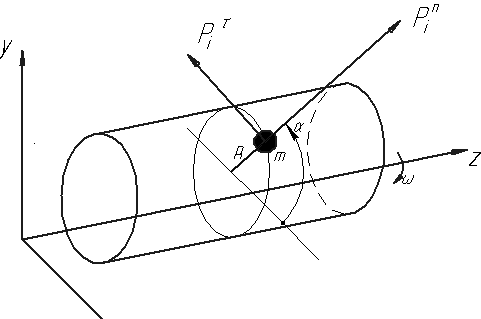
Рис. 7.1. Схема ротора

Спроектируем эти силы на оси х, у, z и определим моменты этих сил относительно осей:

(7.2)

Подставив (7.1) в (7.2) и просуммировав, получим (учитывая, что , )

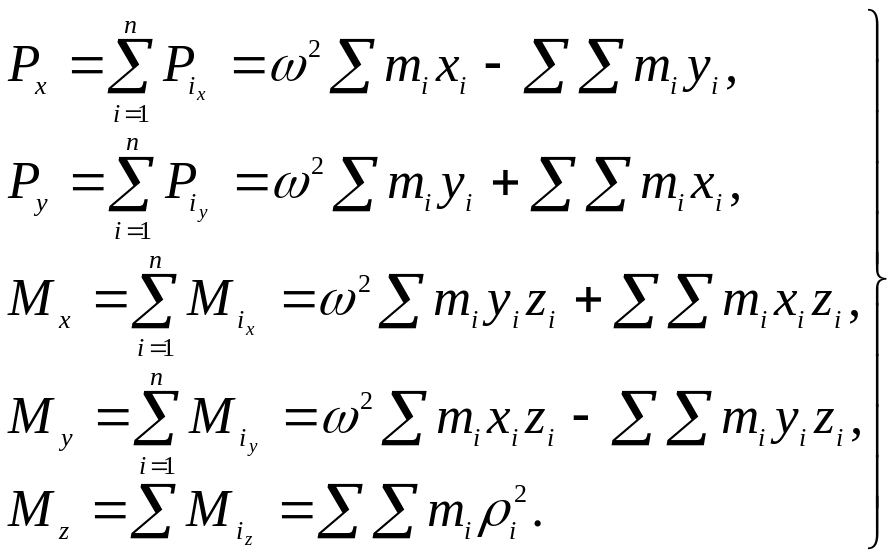
(7.3)

Последнее уравнение в (7.3) можно исключить, так как момент не создает дополнительной реакции в опорах ротора.

Силы и , моменты и равны нулю в том случае, если координаты x и y массы m расположены на оси вращения z (т.е. центр масс ротора неподвижен):

(7.4)

Это есть условие статической уравновешенности ротора.

Моменты и равны нулю, если центробежные моменты инерции ротора равны нулю:

(7.5)

Это есть условие динамической уравновешенности ротора.

Выводы: ротор статически уравновешен, если его центр тяжести расположен на оси вращения; ротор динамически уравновешен, если его ось вращения является главной центральной осью инерции.

Уравновешенность ротора можно охарактеризовать и силовыми параметрами. Он статически уравновешен, если главный вектор сил индукции . Ротор динамически уравновешен, если главный вектор моментов сил инерции .

При проектировании роторов используют условия (7.4) и (7.5). При проверке уравновешенности изготовленных роторов используют условия и . Устранение остаточной неуравновешенности уже изготовленного ротора, возникшей по причинам неточности изготовления, монтажа, из-за неоднородности материала, из которого изготовлен ротор, называется балансировкой. Техника статической и динамической балансировки жестких роторов изложена в [6] и входит в содержание лабораторного практикума по дисциплине «Теория механизмов и машин».

7.3. Уравновешивание вращающихся масс

7.3.1. Уравновешивание масс, находящихся в одной плоскости

Положения отдельных неуравновешенных масс , расположенных на роторе, можно охарактеризовать величинами радиус-векторов относительно оси его вращения. Система вращающихся масс будет уравновешена, если главный вектор сил инерции, действующих на эти массы при их совместном вращении, равен нулю:

,

где – сила инерции, действующая на i-ю массу; – сила инерции уравновешивающей массы , расположенной на расстоянии от оси вращения ротора.

Сила инерции, действующая на i-ю массу, вращающуюся с постоянной скоростью , равна .

Рассмотрим систему, состоящую из трех неуравновешенных вращающихся масс m₁, m₂ и m₃ (рис. 7.2).

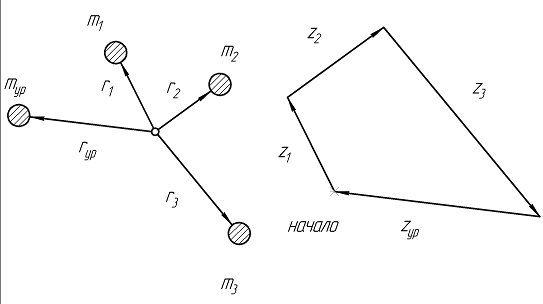
а б

Рис. 7.2. Система неуравновешенных масс (а) и план сил инерции (б)

Условием уравновешенности данной системы масс является уравнение

.

Так как , то это уравнение можно записать в виде

.

Так как (мы рассматриваем вращающуюся систему масс), то

. (7.6)

Уравнение (7.6) можно решить аналитическим и графическим методами.

При аналитическом методе решения составляются уравнения проекций сил на координатные оси, из которых находят являющееся неизвестным последнее слагаемое.

Найдем и графическим методом, то есть построением векторного многоугольника (см. рис. 7.2б), являющегося графической интерпретацией векторного уравнения (7.6). Предварительно выбираем масштаб сил

,

где z₁ – длина вектора, изображающего силу , (мм).

Размерность масштаба (если масса задана в кг, радиус – в м).

Переведем масштабом другие известные слагаемые уравнения (7.6) в векторные отрезки:

Тогда векторное уравнение (7.6) запишется в виде

.

Построив векторный силовой многоугольник (см. рис. 7.2б) в масштабе , из него определим длину вектора . Выбрав из конструктивных соображений величину , вычисляем уравновеши-вающую массу

.

Поместив ее на роторе в направлении вектора на расстоянии от оси вращения, равном длине этого вектора, уравновесим ротор.