32. Удаление вершины в красно – черном дереве.

Удаление из RB-дерева также требует O(log n)времени. Удаление вершины несколько сложнее добавления. Для упрощения удаления в дереве используется вместо значения NIL фиктивные элементы nil[T]. Более того, физически в дереве присутствует один фиктивный элемент, на который ссылаются все листья дерева и узлы, имеющие одного сына. Фиктивный элемент имеет те же поля, что и другие узлы, т.е. p, left, right, key и color, причем в алгоритмах играют роль только поля p и color. Цвет фиктивного элемента всегда черный. Благодаря фиктивному элементу все узлы внутренние.

Операция RB_Delete работает такаже, как и Interative_Tree_Delete. Но вырезав вершину, она вызывает вспомогательную операцию RB_FixUp, которая перекрашивает узлы или производит вращения для восстановления RB-свойств после удаления узла. Эта операция используется, если вырезан черный узел.

RB_Delete (T, z)

1. if left[x] = nil [T] or right[T] = nil [T]

2. then y ← 2

3. else y ← Tree_Successor (z)

4. if left [y] ≠ nil [T]

5. then x ← left [y]

6. else x ← right [y]

7. p [x] ← p[y] вырезание, в фиктивный элемент записывается родитель у

8. if p [y] = nil

9. then root [T] ← x

10. else if y = left [p[y]]

11. then left [p [y]] ← x

12. else right [p[y]] ← x

13. if y ≠ z

14. then key [z] ← key [y]

15. копируем дополнительные данные из вершины у

16. if color [y] = BLACK

17. then RB_FixUp (T, x)

18. return y

Отличия RB_Delete от Interative_Tree_Delete:

1. вместо nil используется nil[T];

2. в строке 7 нет проверки if x ≠nil и p[x]←p[y] выполняется всегда, т.е. фиктивный элемент начинает ссылаться на родителя вырезаемого узла;

3. используется RB_FixUp в случае вырезания черного узла. Вырезание его приводит к нарушению четвертого RB-свойства . Вырезание красного узла не приводит к нарушению RB-свойств.

При удалении черного узла возможны 2 ситуации:

В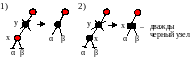 первом случае нарушение можно компенсировать перекрасив узел х в черный цвет. Это позволит ликвидировать и нарушение третьего свойства, если родитель вырезанного узла у – красный.

Во втором случае применяется перестройка в корне поддерева, где возникло нарушение четвертого свойства. Причем узел х считается дважды черным, способным поделиться своей чернотой с вышележащими на пути к нему узлами.

Нужно перестроить вышележащие узлы таким образом, чтобы избавиться от дважды черного узла, не нарушив RB-свойств дерева.

Если х – корень, тогда лишняя чернота просто удаляется из дерева. Иначе выполняется циклическая перестройка корней поддеревьев, лежащих на пути к х, путем перекрашивания и вращений влево или вправо. Перестройка учитывает 4 возможных случая, которые могут встретиться на пути.

Р ассмотрим эти случаи:

Э то наиболее благоприятный случай. Можно перекрасить родителя х в черный цвет, х сделать обычным черным узлом, а w – красным. На этом перестройка заканчивается. Если родитель х – черный, то он становится дважды черным и перестройка поднимается в верхнее поддерево.

Е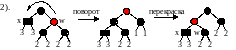 сли новый х – корень дерева, то лишняя чернота просто удаляется из дерева.

Почти случай 1.

Этот случай можно свести к первому, чтобы братом х стал черный узел. Для этого сделаем левый поворот родителя узла х.

3 ). Теперь разберемся со случаями, отличными от 1, т.е. когда сыновья w разного цвета: Перекрасив родителя х в черный цвет, а w – в красный , мы нарушим свойство 3 для w.

П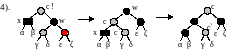 оэтому сделаем сначала правый поворот узла w.

Для случая 4 важно, что правый сын узла w – красный. Перекрашивать нельзя. Левый сын может быть и красным и черным. Опять же действие по схеме случая 1 не годится, т.к. это приведет к нарушению свойства 3.

Тогда произведем вращение влево родителя х. Узел х отдает свою черноту родителю, а правый сын узла w перекрашивается в черный цвет. Узел w берет цвет корня поддерева до поворота.

В этом случае происходит полное поглощение излишней черноты и на этом перестройка прекращается.

Итак, рассмотрев действия в различных случаях, подробно рассмотрим только операцию RB_FixUp (T, x).

RB_FixUp (T, x)

1. while x ≠ root [T] and color [x] = BLACK

2. dv if x = left [p[x]]

3. then w ← right [p[x]]

4. if color [w] = RED случай 2

5. then color [w] ← BLACK

6. color [p[x]] ← RED

7. Left_Rotate (T, p[x])

8. w ← right [p[x]]

9. if color [left [w]] = BLACK and color [right [w]] = BLACK

10. then color [w] ←RED случай 1

11. x ← p[x]

12. else if color [right [w]] = BLACK случай 3

13. then color [left [w]] ← BLACK

14. color [w] ← RED

15. Right_Rotate (T, w)

16. w ← right [p[x]]

17. color [w] ← color [p[x]] случай 4

18. color [p[x]] ← BLACK

19. color [right [w]] ← BLACK

20. Left_Rotate [T, p[x]]

21. x ← root [T]

22. else (симметричный фрагмент с заменой left на right)

23. color [x] ← BLACK

Операция RB_Delete выполняется за O(log n). Обычно производится не более трех вращений.