Алгоритм на псевдокоде

LL1 – поворот

q := p→Left

IF (q→Bal = 0) p→Bal := -1, q→Bal := 1, Уменьш := false

ELSE p→Bal := 0, q→Bal := 0

p→Left := q→Right

q→Right := p

p := q

Аналогично изменяется RR – поворот, LR и RL – повороты не изменяются.

Алгоритм на псевдокоде

RR1 – поворот

q := p→Right

IF (q→Bal = 0) p→Bal := 1, q→Bal := -1, Уменьшение := ЛОЖЬ

ELSE p→Bal := 0, q→Bal := 0

FI

p→ Right:= q→ Left

q→ Left := p

p := q

Алгоритм на псевдокоде

Удаление из АВЛ-дерева (x: Данные, p: pVertex, Уменьшение: boolean)

IF (p = NIL) {ключа в дереве нет}

ELSE IF (p→Data > x) Удаление (x, p→Left, Уменьшение)

IF Уменьшение BL (p, Уменьш) FI

ELSE IF (p→Data < x) Удаление (x, p→Right, Уменьшение)

IF Уменьшение BR (p, Уменьшение) FI

ELSE IF {удаление вершины по адресу p}

q := p

IF (q→Right = NIL) p := q→Left, Уменьшение := ИСТИНА

ELSE IF (q→Left = NIL) p := q→Right, Уменьшение := ИСТИНА

ELSE del (q→Left, Уменьшение)

IF Уменьшение BL (p, Уменьшение) FI

FI

dispose(q)

FI

30. Красно – черные деревья. Свойства. Вращение. Высота красно – черного дерева.

Красно-черные деревья пред­ставляют собой одну из множества "сбалансированных" схем деревьев поиска, ко­торые гарантируют время выполнения операций над динамическим множеством O(log₂n) даже в наихудшем случае.

Красно-черное дерево (red-black tree) - это двоичное дерево поиска, вершины которого разделены на красные (red) и черные (black). Таким образом каждая вершина хранит один дополнительный бит - её цвет.

При этом выполняются определённые требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в два раза.

Каждая вершина красно-черного дерева имеет поля color (цвет), key (ключ), left (левый ребенок), right (правый ребенок) и p (родитель). Если у вершины отсутствует ребенок или родитель, то соответствующее поле содержит NIL.

Двоичное дерево поиска называется красно-черным, если оно обладает следующими свойствами:

1. каждая вершина - либо черная, либо красная ;

2. корень дерева является черным;

3. каждый лист (NIL) - чёрный ;

4. если вершина красная, оба её ребенка чёрные ;

5. все пути, идущие вниз от корня к листьям, содержат одинаковое количество чёрных вершин.

Повороты

Операции над деревом поиска Tree_Insert и Tree_Delete, будучи приме­нены к красно-черному дереву с n ключами, выполняются за время O(log₂n). Поскольку они изменяют дерево, в результате их работы могут нарушаться крас­но-черные свойства. Для восстановления этих свойств мы должны изменить цвета некоторых узлов дерева, а также структу­ру его указателей.

Изменения в структуре указателей будут выполняться при помощи поворотов (rotations), которые представляют собой локальные операции в дереве поиска, сохраняющие свойство бинарного дерева поиска. На рис. показаны два типа поворотов - левый и правый (здесь 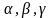- произвольные поддеревья). При выполнении левого поворота в узле х предполагается, что его правый дочерний узел у не является листом nil [T]. Левый поворот выполняется "вокруг" связи между х и у, делая у новым корнем поддерева, левым дочерним узлом которого становится х, а бывший левый потомок узла у - правым потомком х.