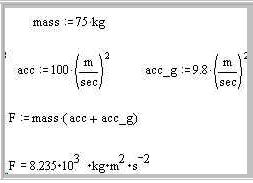Упражнение 2.9. Использование дискретного аргумента для многократных вычислений.

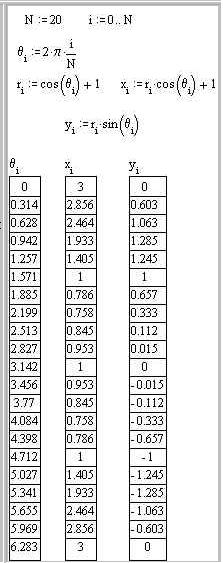
Задача: определить координаты x и y 20 точек кривой r=cos(q )+1, где q =0…2 .

1. Задайте число вычисляемых значений: N:20. 2. Задайте дискретный аргумент и шаг его изменения: i:0..N. 3. Запишите выражение для i-го угла  i:  i:2· p·i/N. Для ввода индекса i при переменной q используйте палитру операторов или клавишу левой квадратной скобки [ [ ]. 4. Запишите выражение для i-й величины r: ri: cos(q i)+1. 5. Запишите выражение для i-й величины x: xi: ri? cos(q i). 6. Запишите выражение для i-й величины y: yi: ri? sin(q i). 7. Выведите на экран значения величин q , r, x, y: q i= ri= xi= yi=.

Обратите внимание, что в этом упражнении i, а не  , определен как дискретный аргумент. Поскольку i принимает только целочисленные значения, что допустимо для нижнего индекса.

Упражнение 2.10. Использование дискретного аргумента для многократных вычислений.

Задача та же: определить координаты x и y 20 точек кривой r=cos(q )+1, где q =0…2 .

1. Задайте число вычисляемых значений: N:20. 2. Задайте дискретный аргумент и шаг его изменения:  :0,2· p /N.. 2· p 4. Запишите выражение для величины r в виде функции от q : r(q ):cos(q )+1. 5. Запишите выражение для x в виде функции от q : x(q ):r(q )· cos(q ). 6. Запишите выражение для y в виде функции от q : y(q ):r(q )·sin( ). 7. Выведите на экран значения величин , r, x, y: q = r(q )= x(q )= y(q )=.

Использование функций позволяет избежать использования нижних индексов.

Упражнение 2.11. Рекурсивное вычисление с одной переменной.

Рекурсивные вычисления применяются для решения конечно-разностных уравнений. Они могут также использоваться для получения приближенных решений для некоторых дифференциальных уравнений. В рекурсивных вычислениях определяется первый элемент массива и затем вычисляются последовательные элементы, основанные на первом элементе

Задача: методом последовательных приближений вычиcлить квадратный корень числа 700.

Классический метод для вычисления квадратных корней состоит в следующем:

Чтобы найти квадратный корень Числа, начните с предполагаемого значения, которое можно рассматривать как начальное приближение к истинному. Затем вычислите новое приближение, основанное на старом приближении, по формуле:

СледующееПриближение= (ПредыдущееПриближение+Число/ПредыдущееПриближение)/2.

И так далее, пока Приближения не сойдутся (то есть не перестанут изменяться при последующих вычислениях).

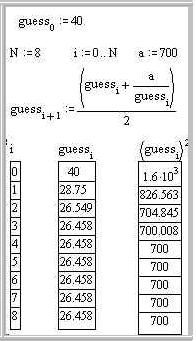
1. Задайте начальное приближение искомой величины: guess0:40. 2. Задайте число приближений: N:8. 3. Задайте дискретный аргумент и шаг его изменения: i:0..N. 4. Задайте число, корень которого будете искать: а:700. 5. Запишите формулу определения квадратного корня: guessi+1:(guessi+a/guessi)/2. 6. Выведите на экран значения величин i, guessi, (guessi)2: i= guessi= (guessi)2=.

Вычисления с единицами измерений, изменение единиц измерения результата вычисления.

После запуска Mathcad в нём доступна полная система единиц измерений. Можно обходиться с ними, как со встроенными переменными. Чтобы связать единицу измерений с числом, достаточно умножить число на ее наименование.

Упражнение 2.12. Использование единиц измерений в выражениях.

1. Введите: mass:75· kg acc:100· m/sec^2 acc_g:9.8· m/sec^2 F:mass·(acc+acc_g). 2. Напечатайте: F=. Mathcad выведет значение силы и единицы ее измерения.

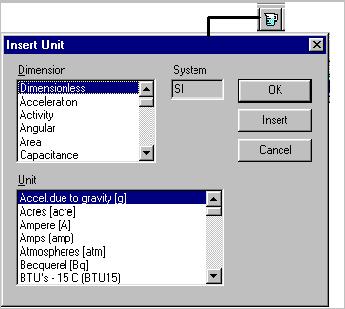
Рис.2.2. Диалоговое окно Вставки единиц измерения.

Mathcad распознает большинство единиц измерений по их общим сокращениям. Проще всего использовать диалоговое окно InsertUnit (Вставить единицы) выбором меню InsertUnit… или нажатием на пиктограмму, изображающую мерную чашку на панели инструментов (см.рис.2.2). Диалоговое окно "Вставить единицы" имеет следующие преимущества:

• Не нужно помнить сокращения Mathcad, используемые для единиц измерений.

• Видны сразу все доступные единицы измерений, соответствующие требуемой размерности.

• Невозможно сделать ошибку, печатая имя.

Диалоговое окно имеет два прокручивающихся списка. Прокручивающийся список Unit (единица измерения) показывает встроенные единицы измерений, соответствующие той физической величине, которая выбрана в прокручивающемся списке Dimension (Размерность).В списке Unit дважды щёлкните на нужной единице измерений. Mathcad вставит эту единицу измерений в место ввода.

Проверка размерности.

Всякий раз, когда вводится выражение, содержащее единицы измерения, Mathcad проверяет его на непротиворечивость размерностей. Если нарушаются правила действий с размерными величинами, Mathcad выдает соответствующие сообщения об ошибках.

6