33.Теоремы Лапласа.

Локальная формула лапласа p(k)=1/sqrt(n*p*q) * ф(x), x=(k-n*p)/ sqrt(n*p*q), ф(х) находится в таблице.

p(k1<=k<=k2)=Ф(х2)-Ф(х1)-функция Лапласа.

34.Случайная дискретная величина.

Случайная величина-величина, которая при проведении опыта принимает то или иное значение заранее неизвестно, какое.

Дискретная случайная величина-величина, которая принмиает счетное множество значений и при этом каждому из значений ставится в соответствие некоторое положительное число так, что сумма этих чисел равна 1.

Закон распределения-таблица, в которой каждому значению х указывается число, в соответствие с заданием.

35.Функция, плотность распределения вероятностей вычисление вероятночти принятия величиной значения из отрезка а в.

Функция распределения-некоторая неотрицательная функция, заданная формулой F(x)=p(X<x).

Пусть задано неотрицательное p(X)>=0, определенная на всей числовой оси такая, что интеграл от нее будет равен 1, тогда функция F(x)=ИНТЕГРАЛ p(t)dt, обладает всеми свойствами функции распределения, в этом случае функция р(х) называется плотностью вероятности случайной величины.

38.Числовые характеристики случайных величин. Дисперсия.

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Дисперсия любой случайной величины неотрицательна. Если дисперсия случайной величины конечна, то конечно и её математическое ожидание. Вычисляется по формуле: Д[x]=интеграл x^2*p(x)dx-M[x]^2.

37.Мат.Ожидание.

Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины.

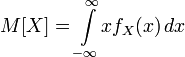
• Математическое ожидание числа есть само число.

• Математическое ожидание произведения двух независимых случайных величин 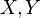  равно произведению их математических ожиданий

Математическое ожидание линейно