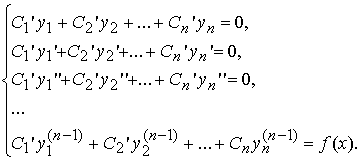1.Понятие дифф. Уравнения, его решения.Дифф уравнения, как мат.Модели физ.Процессов.

Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).В зависимости от комбинаций произодных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.

2.Дифф уравнения первого порядка. Их геометрическая интерпретация.Построение дифф.Уравнения заданного семейства кривых.

Дифференциальное уравнение первого порядка, содержит:  1) независимую переменную  ; 2) зависимую переменную   (функцию); 3) первую производную функции:  .

В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная  , и не было производных высших порядков –  ,   и т.д.

Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество функций  , которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.

Геометрический смысл-образования одной и той же прямой, называемой изоклином.

3.Дифф.уравнения с разделяющимися переменными.

 Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.

4.Однородные дифф.Уравнения.

Обыкновенное уравнение первого порядка   называется однородным относительно x и y, если функция   является однородной степени.

5.Дифф. Уравнения, приводимые к однородным.

6. Линейные уравнения первого порядка. Метод Бернулли.

Линейным дифференциальным уравнением первого порядка называется уравнение вида

y ‘ + f(x)*y=ф(x). Удобным способом решения линейных уравнений является метод Бернулли. Пусть дано уравнение (1). Решение этого уравнения будем искать в виде произведения двух функций: y=u*v,где u=u(x) и v=v(x). Далее подставляем это значение вместо y и все решение сведется к решению системы уравнений с разделяющимися переменными.

7.Вариация произвольной постоянной.

Предположим, что известна фундаментальная система y1(x), y2(x),..., yn(x) решений соответствующего однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) ,

где C1(x), C2(x) , ... , Cn(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Справедливо следующее утверждение.

Пусть y1(x), y2(x),..., yn(x) — фундаментальная система решений однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде

y*(x) = y(x,C1,..., Cn) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) .

Неизвестные функции C1(x), C2(x) , ... , Cn(x) находятся из системы.