7. Курсовое проектирование

Курсовое проектирование по ОТУ подразумевает законченную процеду­ру проектирования устройства управления подвижным объектом. В него входят все составные части реальной разработки системы управления (СУ):

1. разработка блок - схемы системы управления;

2. описание объекта управления (ОУ);

3. определение наблюдаемых и управляемых переменных;

4. создание математической модели ОУ;

5. построение математической модели системы;

6. анализ характеристик СУ;

7. синтез корректирующих устройств.

7.1. Разработка блок-схемы системы управления

В настоящем разделе формулируется проблема, которую должна ре­шить система автоматического управления, определяются входные и выход­ные переменные ОУ, составляется структурная схема предполагаемой систе­мы управления.

В качестве примера рассмотрим задачу обеспечения вертикальной ус­тойчивости велосипеда. Подобные объекты принадлежат к классу неустой­чивых объектов, получившему название «перевернутый маятник».

Чтобы удержать велосипед в вертикальном положении, велосипедист поворачивает руль в направлении падения. Примем руль за управляющую (входную) переменную. Выходной переменной будет угол у отклонения от вертикальной плоскости. Этот угол легко измерить: для этого достаточно, например, на ось потенциометра повесить грузик, а ось расположить гори­зонтально. Получилось звено обратной связи. Чтобы поворачивать руль, за­крепим на нем шестеренку, сцепленную с шестерней, сидящей на валу элек­тродвигателя постоянного тока. Сам электродвигатель закрепим на раме - на втулке переднего колеса. Вместе с рулем это будет исполнительный меха­низм (рис. 7.1).

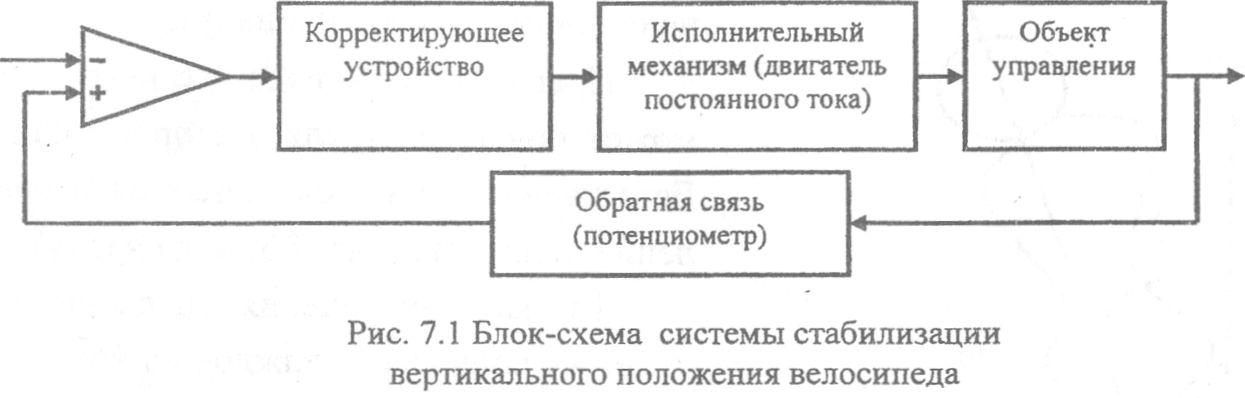
Устройством управления в такой системе будет дифференциальный усилитель, на прямой вход которого подается сигнал задающего устройства (велосипедиста), а на инверсный - напряжение потенциометра обратной свя­зи. Тогда усилитель одновременно будет выполнять функцию устройства сравнения. Но для управления неустойчивым объектом этого мало: в замкну­том состоянии такая система останется неустойчивой. Поэтому главной зада­чей курсового проекта является синтез корректирующего устройства, спо­собного обеспечить заданное качество управления. Для решения этой задачи необходимо получить математическую модель всех блоков системы и про­вести анализ ее динамических характеристик. Разработанная блок-схема при­ведена на рис. 7.1.

7.2. Составление математической модели оу

Для построения математической модели динамических звеньев исполь­зуются дифференциальные уравнения, получаемые на основе физических законов механики, термодинамики, оптики.

Примеры составления таких дифференциальных уравнений можно най­ти, например, в рекомендованной литературе. Как правило, это классические объекты автоматического управления: ракета, самолет, спутник, торпеда. Авторы рассмотрят более простой и знакомый пример - велосипед.

Математическая модель системы «велосипед + велосипедист». При смещении центра тяжести велосипедиста относительно вертикальной оси возникает крутящий момент, приводящий к падению:

где h — расстояние от центра масс до точки касания с землей; т — масса

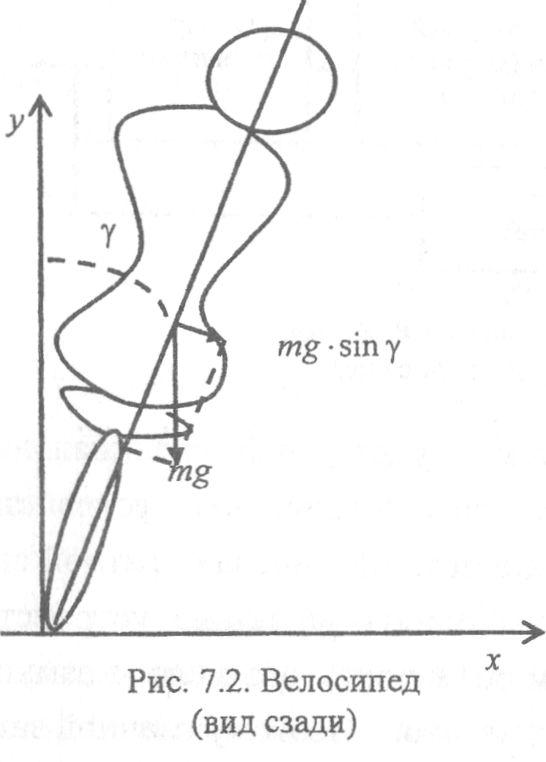
велосипеда; g - ускорение свободного падения; у - угол наклона (рис. 7.2).

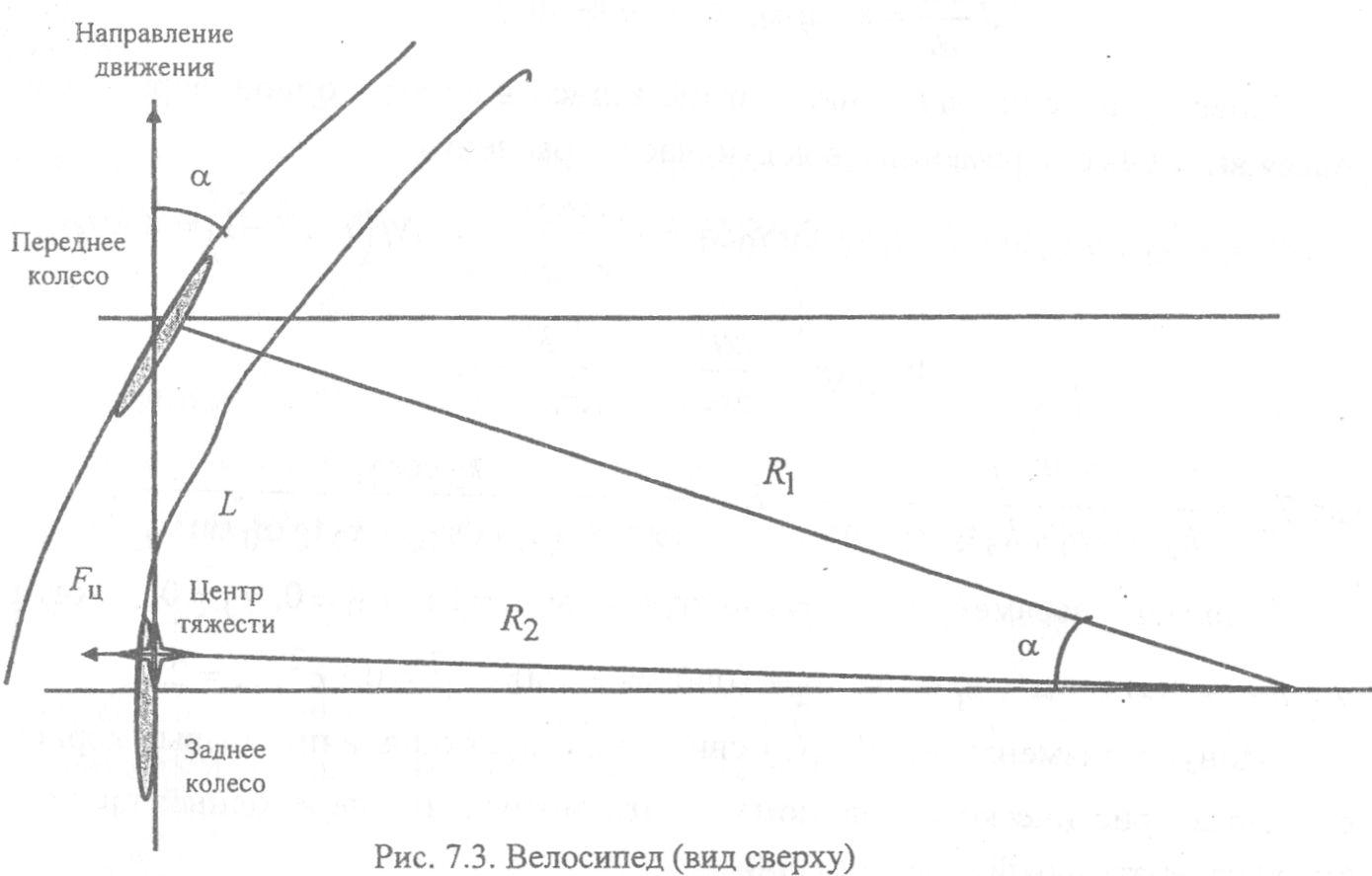
Препятствовать падению велосипедист может поворотом руля в сторону падения. Естественно, при этом меняется и направ­ление движения (рис. 7.3, вид сверху).

Так как направления движения обоих колес не совпадают, каждое из колес долж­но двигаться по траекториям, касательные к которым в точках контакта с землей совпа­дают с плоскостью колеса. Поскольку такое несогласованное движение невозможно, поворот переднего колеса вызовет поворот рамы и с нею - поворот заднего. Заднее колесо при этом получает боковое про­скальзывание, что можно наблюдать по фонтану брызг при повороте на луже. Это же является причиной заноса автомобиля, поворачивающего на большой скорости.

В результате траекторией движения обоих колес будет окружность с од­ним и тем же центром, но с разными радиусами: у переднего колеса радиус поворота больше, чем у заднего

Если расстояние между точками касания колес с землею обозначить L, тоВращение приведет к появлению центробежной

силы, приложенной к центру тяжести.

Положение центра тяжести зависит от наклона тела велосипедиста. Для варианта «мастер» эта точка близка к середине расстояния между точками

касания с землей, для варианта «чайник» центр тяжести (точнее, его проек­ция на горизонтальную плоскость) практически совпадает с точкой касания земли вторым колесом. Вернемся теперь в вертикальную плоскость и опре­делим радиус вращения центра тяжести велосипедиста.

При малых углах наклона:Возникающая

Положив в уравнении (7.1), имеем:

при таком вращении центробежная силаТеперь уравнение движения будет иметь вид

Согласно рис. 7.1, выходная величина ОУ - угол наклона велосипеда у, входная - угол поворота руля а. Разделить переменные в несепарабельном уравнении можно, если воспользоваться первыми членами разложения в ряд Тейлора:

Теперь уравнение движения можно записать в операторной форме, пе­ренеся выходные переменные в левую часть уравнения:

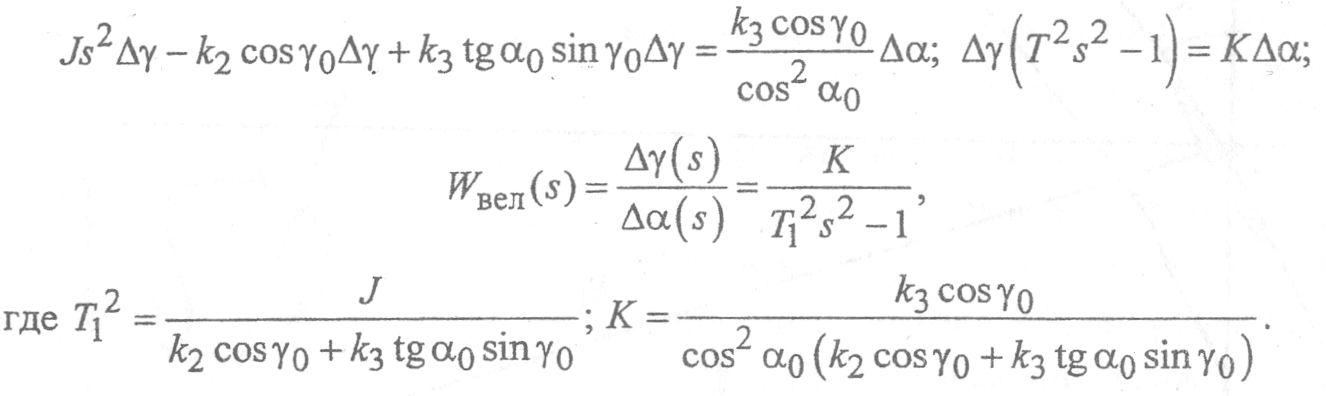
Зададим параметры:тогда

Минус в знаменателесвидетельствует о наличии правых корней

его характеристического полинома. А это значит, что переходный процесс будет колебательный и расходящийся.

Передаточная функция разомкнутой системы управления. Итак, получив передаточную функцию объекта управления

зададим передаточные функции остальных звеньев системы.

Вычтем из последнего уравнения уравнение статики:

• Электродвигатель с редуктором. При батарейном питании выбираем двигатель постоянного тока. Его динамика определяется двумя постоянными времени: электромеханической постоянной, зависящей от момента инерции якоря, и электромагнитной постоянной времени, зависящей от ин­дуктивности ротора. Еслииотличаются меньше, чем на порядок, их совместное действие описывается типовым колебательным звеном

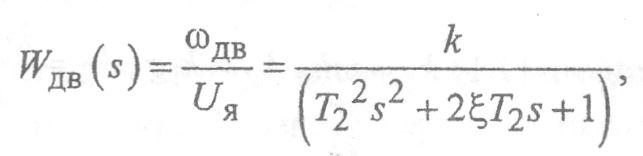
где к - статический коэффициент преобразования входного напряжения в скорость вращения; вместе с редуктором примем к = 1;- посто­

янная времени двигателя, реальная величина Т2 меньше постоянной времени велосипеда на два порядка. Чтобы почувствовать влияние двигателя, примем

- коэффициент затухания, обычно

Если выходной величиной считать не скорость вращения двигателя, а угол его поворота, в передаточную функцию следует добавить оператор ин­тегрирования 1 / s . Часто функцию интегрирования отводят редуктору. Тогда

• Усилитель. В статической системе коэффициент усиления (всей пря­мой цепи) выбирается исходя из допустимой ошибки управления. Если ошибку управления z(t) представить в виде ряда Маклорена:

(х - входное воздействие), то для

статической системы коэффициенты ошибки могут быть получены из передаточной функции W(s) разомкнутой системы:

- коэффициент статической ошибки;

- коэффициент ошибки по скорости (и- коэффи­ циенты числителя и знаменателя W(s) при).

Тогда в статической системе ошибка управления в статике:

Для систем с интегратором (астатических) ошибка в статике равна нулю при любом коэффициенте усиления. Однако коэффициент ошибки по скоро­сти Cj = 1 / к. Если принять максимальную начальную скорость падения велосипедиста равной 1 рад/с, для обеспечения максимального отклонения от вертикали на ±2° получим:

Окончательно передаточная функция разомкнутой системы: