3. Корневые методы анализа

1. Связь корней и временных процессов

Реакцию системы на входное воздействиеможно записать в следующей форме:

, (3.1)

где – полином, отражающий воздействие начальных условий.

Упростим это выражение, приняв нулевые начальные условия и входное воздействие :

.

Полином является дробно-рациональной функцией, которую можно разложить на множители, где– корни характеристического уравнения.

Тогда можно представить в виде, известном кактеорема разложения (при некратных корнях):

. (3.2)

Представление реакции системы в виде суммы реакций, вызванных каждым из корней полиномов G(s) иD(s), позволяет оценить вклад любого корня, выделить наиболее "вредные" и принять меры по их нейтрализации.

Для комплексно-сопряженных корней уравнение (3.2) приобретает вид:

+, (3.3)

–затухающий процесс, если вещественные части всех корнейотрицательные, т. е. лежат в левой полуплоскости корней. Даже один правый корень приведет к расходящемуся процессу – система станет неустойчивой. Чем меньше по модулю вещественная часть корня, тем медленнее затухает соответствующая этому корню экспонента. Поэтому длительность переходного процесса определяется удаленностьюот мнимой оси самого близкого к ней корня (рис. 3.1). Это расстояние принято за меру качества системы управления и носит названиестепени устойчивости :.

Вторым корневым показателем качества служит тангенс максимального угла, образованного отрицательной вещественной полуосью и прямой, проведенной из начала координат. Он характеризует колебательность системы и называется степенью колебательности :.

Чем больше ,тем большее число колебаний будет у переходного процесса за время регулирования.

При записи комплексных корней в видетеряется самая важная особенность корня – его физический смысл, его размерность. Из (3.3) понятно, что мнимая часть корня есть не что иное, как угловая частота гармонического колебания, где– период колебания. Поэтому вместо принятых (например, в Matlab) обозначений осей корневого годографаImиReбудем использовать для мнимой оси обозначениеа для вещественной оставим(записьпроще, чем).

2. Корневой годограф

Корневой годограф– траектория движения корней в комплексной области при изменении одного из параметров системы. Чаще всего под изменяемым параметром подразумеваетсякоэффициент петлевого усиления.Однако при синтезе системы заданного качества желательно знать, к чему приведет перемещение того или другого корня звена коррекции. Покажем, как строится такой годограф.

Пусть передаточная функция замкнутой системы , тогда полюсы замкнутой системы являются корнями уравнения:

. (3.4)

Matlabпо умолчанию строит корневой годограф именно по этому уравнению, выбирая в качестве параметра. Если вы хотите построить годограф по другому параметру, например, по одному из нулей, надо представить (3.4) в виде:, что можно выполнить и вручную:

.

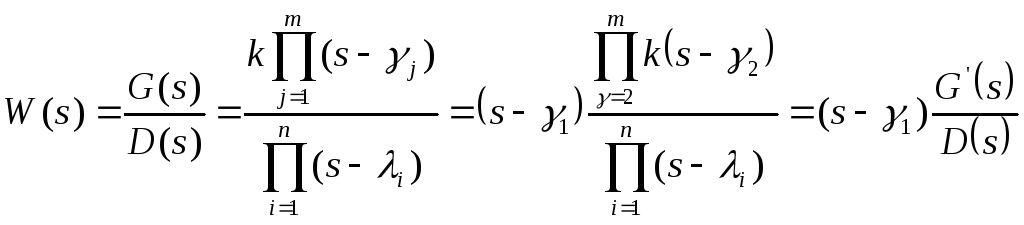После подстановки в (3.4) получим:

, ,

. (3.5)

Так как Matlab ведет построение годографа только для положительных γ, знак в формуленадо поменять на положительный.

Существует несколько простых правил, позволяющих "вручную" построить корневой годограф по параметру :

1. Все полюсы замкнутой системы при совпадают с полюсами разомкнутой системы.

2. При полюсы замкнутой системы стремятся кнулямразомкнутой, т. е. годограф начинается изполюсовразомкнутой системы и заканчивается в еенулях.

Все последующие правила определяют траекторию оставшихся корней: из требования физической реализуемости степень полинома числителя не должна превосходить степень полинома знаменателя, поэтому "лишними" всегда оказываются полюсы.

3. Полюсы на вещественной оси при увеличении движутся попарно навстречу друг другу, причем крайний справа корень движется влево. Участки вещественной оси, по которым двигаются пары корней, никогда не перекрываются: происходит чередование занятых и свободных участков, причем на занятых участках слева расположено нечетное количество корней.

4. При «столкновении» пары корней (полюсов) на вещественной оси они переходят в комплексную плоскость, двигаясь с зеркальной симметрией (результат комплексного сопряжения) относительно вещественной оси к своим асимптотам или к нулям.

5. Асимптоты корней образуют звезду с центром в центре тяжести корней (х_с,0), где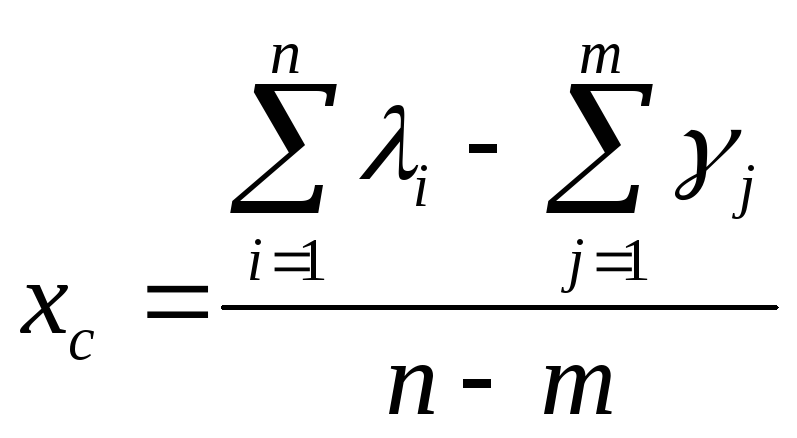, и равными углами между асимптотами. Количество асимптот равноn-m, гдеn– число полюсов,m– число нулей.

На рис. 3.2-3.5 приведены корневые годографы для систем от первого до третьего порядков.

Поведение одного корня для системы первого порядка легко получить по формуле замыкания: . Пусть=, тогда:

, где ,.

Чем больше контурный коэффициент усиления, тем меньше величина эквивалентной постоянной времени , и, соответственно, тем дальше от мнимой оси уходит корень. Аналогично определяется поведение корней для систем более высокого порядка.

При n=3 асимптоты делят комплексную плоскость на три сектора по 120(рис. 3.4).

Если пара полюсов комплексная (рис. 3.5), то хотя асимптоты и остались на прежнем месте, но друг с другом объединяется уже другая пара корней.

Добавим к двум полюсам один ноль γ (рис. 3.6, аиб).

Если справа от нуля всего один полюс, то этот полюс бежит к нулю, образуя диполь – одинаковые множители в числителе и знаменателе , которые практически не оказывают влияния на переходный процесс.

Е

n=2

сли справа от нуля два полюса (рис. 3.6,б), по правилу 4 они двигаются навстречу друг к другу и переходят в комплексную плоскость. Оставаясь комплексно-сопряженными, оба корня возвращаются на вещественную ось слева от нуля. Поскольку на любом участке вещественной оси может двигаться только один корень (правило 3), их пути расходятся: один движется направо к нулю, второй – по единственной асимптоте к.

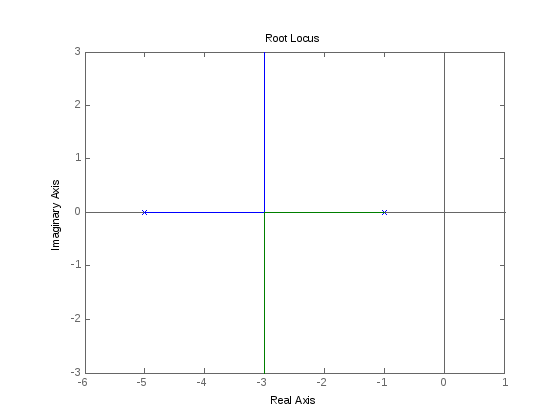
Рис. 3.2. Годограф для системы первого Рис. 3.3. Годограф для системы второго порядка порядка

Рис. 3.4. Годограф для системы третьего порядка, все корни вещественные

Рис. 3.5. Годограф для системы третьего порядка, пара корней – комплексны

Рис. 3.6, б. демонстрирует метод компенсации одним нулем сразу двух нежелательных полюсов. Чем дальше влево отодвинуть ноль, тем по большему радиусу будут двигаться влево правые полюса, тем устойчивее может стать система. Однако расширение этого круга может привести и к нежелательной колебательности замкнутой системы: все зависит от того, в каких точках этих окружностей находятся корни при выбранном вами коэффициенте усиления. Ответ на этот вопрос может дать годограф, построенный по параметру γ (см. (3.5)) при фиксированном. Такой годограф приведен на рис. 3.7,б.

а б

Рис. 3.6. Компенсация одним нулем двух нежелательных полюсов

Рис. 3.7. а– годограф по параметрус наложением истинного положения корней при выбранном(точки),б– годограф по параметруγ

Рис. 3.8 и 3.9 построены для систем с n=3 иm=2, но на рис. 3.8 все полюсы вещественные, а на рис. 3.9 два полюса комплексные. По правилу 3 для рис. 3.8 участки вещественной оси справа от обоих нулей должны быть свободны: справа от них находится четное число корней. Поэтому правый нуль может объединиться только с полюсом слева от него (3). Два крайних справа полюса (1 и 2) двигаются навстречу друг другу и переходят в комплексную плоскость. Один из этих полюсов должен двигаться к оставшемуся нулю, а второй, не найдя себе пары, устремляется в бесконечность по единственной асимптоте.

На рис. 3.9 ситуация изменилась: справа от первого нуля стоит всего один полюс, и при увеличении петлевого усиления он стремится к нулю. Пара комплексных полюсов движется аналогично предыдущему случаю.

3. Физическая реализуемость, грубость и чувствительность

Передаточная функция считается физически осуществимой, если степень числителяне превышает степень знаменателя:В такой системе относительный порядок неотрицателен,

Система называется грубойилиробастной, если малое изменение ее параметров не приводит к качественному изменению ее свойств, например, устойчивую систему делает неустойчивой. Чаще всего грубость нарушается в случае наличия близких правых корней в числителе и знаменателе. Казалось бы, проще всего мешающий правый полюс (в знаменателемножитель вида) скомпенсировать равным ему нулем, введя такой же множитель в числитель.Так делать нельзя. Покажем это на примере звена первого порядка с полюсом λ=-1/5:. Так как звено устойчиво, при компенсации полюса равным ему нулем () его импульсная переходная функция (см. 3.2) будет:

==0;

При погрешности в установке нуля компенсатора числитель в последнем выражении уже не будет равен нулю, появится затухающаяэкспонента, амплитуда которой будет тем меньше, чем точнее выполнен компенсатор.

Если же λ=+1/5, показатель экспоненты меняет свой знак и стоящий перед ней коэффициент (если он не равен нулю) уже не играет никакой роли: система все равно будет неустойчива.

В замкнутой системе полюсы при изменении kдолжны двигаться к неподвижным нулям, что и обеспечивает компенсацию полюсов даже при неточном задании нулей. Однако и это стабилизирующее свойство замкнутых систем не помогает в случае использования правых нулей: правые полюсы движутся к правым нулям так медленно, что достигают их только приk=∞.

Корневой годограф позволяет оценить еще одно важное свойство динамических систем – чувствительность к возможным отклонениям их параметров.

При проектировании устройств автоматики используемая модель может весьма существенно расходиться с реальным объектом, в связи с чем и возникает необходимость проверки чувствительности к возможным отклонениям ее параметров. Причиной отклонения параметров может быть не только неточность задания параметров, но и изменение их в ходе эксплуатации. Подобная проверка аналогична климатическим испытаниям вновь разработанного прибора, при которых требуется убедиться в его работоспособности во всем возможном диапазоне изменения температуры, влажности и пр. Поэтому в теории чувствительности наиболее развитыми методами являются методы исследования зависимости изменения свойств системы от изменения ее параметров. При этом известны оценки параметрической чувствительности практически для всех форм представления динамических систем (временной, частотной, корневой, по собственным числам матрицы состояния и пр.).

В технике под чувствительностью понимается мера восприятия входных сигналов прибором или системой. Соответственно, под параметрической чувствительностью понимают меру восприятия отклонений параметров системы от номинальных значений.

Иными словами, если есть некоторый показатель качества , зависящий от вектора состоянияи от вектора параметров:, то чувствительностьk-того порядка определяется какk-тая частная производная по вектору параметров:.

Рассмотрим чувствительность системы с позиции корневого годографа. Анализ корневого годографа удобно провести в Matlab либо с использованием утилиты SISO Design tool из пакета Control System toolbox, либо с помощью команды rlocus(sys). Если в SISO Design tool на корневой годограф накладываются маркеры положения корней для выбранного коэффициента усиления, то в годографе rlocus такая возможность не предусмотрена (но можно в выбранной точке траектории посмотреть коэффициент усиления и значение корня щелчком левой кнопки мыши). Кроме того, Matlab самостоятельно выбирает шаг изменения коэффициента петлевого усиления для наиболее точного построения годографа. Эта особенность мешает обнаружить участки повышенной чувствительности корней к изменению усиления. Рассмотрим систему, имеющую один нуль и два полюса: . Ее годограф представлен на рис. 3.10.

Рис. 3.10. Корневой годограф: а– с автоматическим выбором шага поk (командаrlocus(sys));б– с заданным шагом в 2 дБ (командаrlocus(sys,k))

Поскольку нас интересует параметрическая чувствительность системы, выберем для примера в качестве варьируемых параметров мнимую составляющую введенных корней и коэффициент петлевого усиления (рис. 3.11,б).Теперь о чувствительности к варьируемым параметрам можно судить по разреженности линий в разных зонах.Стрелками отмечены зоны наивысшей чувствительности.

а

б

Рис. 3.11. а– корневой годограф исходной системы;б– семейство корневых годографов при варьировании исследуемого параметра

Недостатком такого представления является отсутствие информации об истинном положении корней при выбранном коэффициенте усиления. Устранить этот недостаток можно следующим образом: нанесем на корневой годограф точками положение корней при выбранных коэффициентах усиления с помощью команды plot:

[P k]=rlocus(sys,k);% получение матрицы корней и вектора k

rlocus(sys,k); % построение корневого годографа

hold on

plot(P(:,i),’.k’); % отметить положение корней черными

% точками, i – порядковый номер в

% векторе коэффициентов усиления

Результат описанной процедуры формирует номограмму рис. 3.12.

Точки, соответствующие равным коэффициентам усиления, образуют траектории перемещения корней при изменении мнимой части комплексно-сопряженных корней. С помощью этой номограммы можно не только оценить чувствительность системы в той или иной зоне корней, но и выбрать наилучшие параметры системы.

Рис. 3.12. Номограмма корней

Сформулируем рекомендации по улучшению качества системы с использованием корневого годографа:

1. Компенсация правых полюсов правыми нулями недопустима.

2. Смещение влево центра тяжести корней (центра звезды асимптот) равносильно смещению вправо мнимой оси, что само по себе увеличит степень устойчивости η. Поскольку левые нули смещают центр асимптот вправо, а полюса – влево, сумма модулей полюсов корректирующего устройства должна быть больше суммы модулей его нулей.

3. Если необходимо скомпенсировать двумя нулями два полюса, удобнее использовать комплексно – сопряженные нули: это значительно облегчает формирование диполей именно с выбранными полюсами.

Резюме: любое исследование динамических систем базируется на специфическом математическом аппарате, обеспечивающем наглядное всестороннее рассмотрение их свойств с достаточно простым переходом из одной формы представления в другую. Скопируйте приведенные ниже "шпаргалки" (рис. 3.13 и 3.14) основных характеристик систем и соответствующие им командыMatlab– они послужат вам удобным словарем при выполнении лабораторных работ и курсовом проектировании.