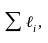- •1 Гидравлический расчЁт каналов при равномерном движении
- •1.1 Общие положения по проектированию и гидравлическому
- •1.2 Гидравлический расчёт магистрального канала
- •1.2.1 Выбор коэффициента шероховатости и коэффициента
- •1.2.2 Определение расчётной скорости потока в магистральном
- •1.2.3 Определение поперечных размеров магистрального канала в
- •1.2.4 Проверка магистрального канала на пропуск форсированного
- •1.3 Гидравлический расчёт сбросного канала
- •1.3.1 Исходные данные
- •1.3.2 Порядок расчёта сбросного канала
- •2 Расчёт неравномерного установившегося
- •2.1 Общие положения
- •2.2 Определение характера и типа кривой свободной поверхности
- •2.3 Расчёт кривой свободной поверхности по способу
- •3 Гидравлический расчёт сопрягающего
- •3.1 Общие положения
- •3.2 Расчёт входной части быстротока
- •Расчёт лотка быстротока
- •3.4.Расчёт выходной части быстротока
- •3.4.1. Установление формы сопряжения потоков в нижнем бьефе
- •3.4.2. Гидравлический расчёт водобойной стенки
2.2 Определение характера и типа кривой свободной поверхности
воды
Для установления характера и типа кривой свободной поверхности в МК необходимо определить критическую глубину hкр и критический уклон iкр.
Критическая глубина определяется методом подбора из уравнения
|
где = 1,051,10 – коэффициент Кориолиса.
Q - максимальный расход воды в МК;
кр = (b+mhкр)hкр-площадь живого сечения при критической глубине;
Bкр = b+2mhкр - ширина по урезу воды при критической глубине.
Задаются рядом
значений глубин h
< h0,
подсчитывают
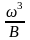 .
Расчёт ведут методом подбора до тех
пор, пока не будет подобрана такая
глубина h
, при которой
.
Расчёт ведут методом подбора до тех
пор, пока не будет подобрана такая
глубина h
, при которой
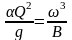 .
.
Данная глубина
является искомой hкр.
Для сокращения расчётов можно построить
график
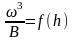 (рисунок 6) и из него по
(рисунок 6) и из него по
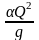 определяется hкр.
Для построения графика расчёты удобно
вести в табличной форме (таблица
3).
определяется hкр.
Для построения графика расчёты удобно
вести в табличной форме (таблица
3).
Таблица 3 - К определению hкр в МК
h, |
=(b+mh)h, |
B=b+2mh, |
|
, |
, |
м |
м2 |
м |
|
м5 |
м5 |
h1=0,5 |
4 |
9 |
64 |
7,11 |
29,42 const
|
h2=0,7 |
5,88 |
9,8 |
203,29 |
20,80 |
|
h3=0,8 |
6,88 |
10,2 |
325,66 |
31,92 |
|
h4=0,78 |
6,67 |
10,12 |
296,74 |
29,32 |
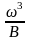
Критический уклон определяется из формулы Шези
где
|
Кривая свободной
поверхности в МК
с уклоном 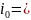
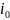 =0,0001369
и глубинами
=0,0001369
и глубинами
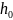 =2,13м,
=2,13м,
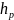 =2,769м,
критическим уклоном
=2,769м,
критическим уклоном
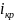 =0,00479
и
=0,00479
и
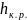 =0.78
– это кривая подпора типа
=0.78
– это кривая подпора типа
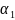 (рисунок 5).
(рисунок 5).
2.3 Расчёт кривой свободной поверхности по способу
Б.А. Бахметева
В основе способа лежит показательный «закон» для модулей расхода, установленный Б.А. Бахметевым для реальных русел
|
|
|
|
|
|
где
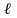 -
длина расчётного участка между сечениями
1-1
и 2-2
с глубинами h1
и h2
(нумерация
сечений и глубин должна быть по течению);
i0,
h0
- уклон дна
и глубина в МК
при равномерном движении.
-
длина расчётного участка между сечениями
1-1
и 2-2
с глубинами h1
и h2
(нумерация
сечений и глубин должна быть по течению);
i0,
h0
- уклон дна
и глубина в МК
при равномерном движении.
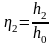 и
и
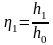 - относительные глубины в сечениях 1-1
и 2-2
расчётного участка;
- относительные глубины в сечениях 1-1
и 2-2
расчётного участка;
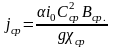 - средний уклон
трения, который определяется по параметрам
Сср,
Вср,
χср,
, подсчитанным
по средней глубине на участке;
- средний уклон
трения, который определяется по параметрам
Сср,
Вср,
χср,
, подсчитанным
по средней глубине на участке;
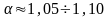 -
коэффициент Кориолиса;
-
коэффициент Кориолиса;
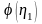 и
и
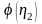 - табличные функции Б.А. Бахметева,
которые определяются по таблице Б1 в
Приложении Б /2/.
- табличные функции Б.А. Бахметева,
которые определяются по таблице Б1 в
Приложении Б /2/.
|
где
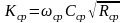 -
расходная характеристика, определяется
по hср;
-
расходная характеристика, определяется
по hср;
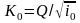 -
расходная характеристика, соответствующая
нормальной глубине при равномерном
движении воды в канале.
-
расходная характеристика, соответствующая
нормальной глубине при равномерном
движении воды в канале.
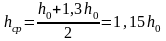 =1,15·2,13=2,44м.
=1,15·2,13=2,44м.
Зная
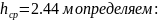
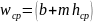 =(7+2·2.44)·2.21=28,98
=(7+2·2.44)·2.21=28,98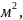
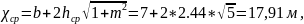
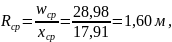
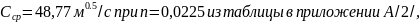
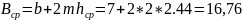 м,
м,
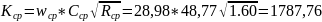 м3/c,
м3/c,
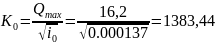 м3/c,
м3/c,
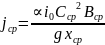 =
=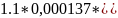 =0.0343,
=0.0343,
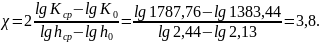
Таблица 4 - Расчёт кривой свободной поверхности в МК по способу
Б. А. Бахметева
№№ уч-ков |
h2, |
h1, |
η2 |
η1 |
hcр |
ωср, |
Вср, |
χср, |
Rср, |
Сср, |
Кср, |
x |
|
|
|
ℓ, |
|
м |
м |
|
|
м |
м2 |
м |
м |
м |
м0,5/c |
м3/c |
|
|
|
|
м |
м |
|
1 |
2,77 |
2,67 |
1,30 |
1,25 |
|
|
|
|
|
|
|
|
|
0,202 |
0,230 |
1180,54 |
- |
2 |
2,67 |
2,57 |
1,25 |
1,20 |
2,44 |
28,998 |
16,76 |
17,91 |
1,60 |
48,77 |
1787,76 |
3,8 |
0,343 |
0,230 |
0,259 |
1195,40 |
2375,94 |
3 |
2,57 |
2,47 |
1,20 |
1,15 |
|
|
|
|
|
|
|
|
|
0,259 |
0,313 |
1565,32 |
3941,26 |
4 |
2,47 |
2,42 |
1,15 |
1,13 |
|
|
|
|
|
|
|
|
|
0,313 |
0,370 |
1149,28 |
5090,54 |
На последнем 4 расчетном участке разность глубин в сечениях изменена и принята равной h=0,05 м ,что позволило получить
=5090,54м,близкой
к длине МК 5000 м, и определить глубину
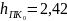 м,без
решения обратной задачи.
м,без
решения обратной задачи.
Используя исходные данные и результаты расчёта неравномерного движения воды (таблица 4), в масштабе строится продольный профиль МК, на котором наносятся кривая свободной поверхности воды при неравномерном движении и линии нормальных и критических глубин. Построении продольного профиля в масштабе: вертикальном М 1:50, а горизонтальном М 1:20000.Из продольного профиля определяем м.

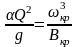 ,
,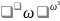
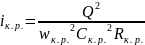 =
=
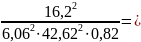 0,00479,
0,00479,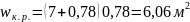 ,
,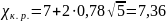 м,
м,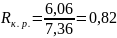 м,
м,
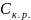 =42,62
=42,62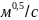 .
.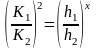 ,
,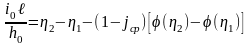 ,
,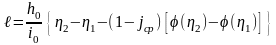 ,
,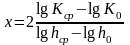 ,
,