
- •12. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры. Понятие функции одной переменной
- •Способы задания функций:
- •Основные свойства функций
- •13. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая). Элементарная функция
- •Основные элементарные функции
- •16. Предел последовательности при и предел функции при . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции). Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •17. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать). Предел функции в точке
- •Основные теоремы о пределах. Признаки существования предела
- •Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.
- •Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.
- •Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.
- •Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно малыми и бесконечно большими величинами
- •19. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замечательный предел.
- •20. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры. Непрерывность функции
- •Свойства функций, непрерывных в точке
- •1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
- •2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
- •Точки разрыва функции
- •Свойства функций, непрерывных на отрезке
- •21. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. Определение производной
- •Задача о касательной
- •22. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Понятие дифференцируемости функции
- •Связь между дифференцируемостью функции и ее непрерывностью
- •23. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •24. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции. Производные основных элементарных функций (таблица производных)
- •Производная сложной функции
- •25. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
- •26. Достаточные признаки монотонности функции (один из них доказать). Признаки возрастания и убывания функции.
- •27. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
- •28. Достаточные признаки существования экстремума (доказать одну из теорем).
- •29. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.
- •30. Общая схема исследования функций и построения их графиков. Пример.
- •31. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия. Основные понятия. Частные производные
- •Частные производные функции двух переменных
- •Экстремум функции двух переменных
- •Инвариантность формы дифференциала
- •Приближенные вычисления с помощью дифференциала
- •34. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать). Понятие первообразной и неопределенный интеграл
- •Свойства неопределенного интеграла
- •35. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
- •36. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
- •Методы вычисления определенного интеграла
- •37. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
- •Геометрический смысл определенного интеграла.
- •Экономический смысл определенного интеграла.
- •Свойства определенного интеграла
- •38. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона—Лейбница. Определенный интеграл с переменным верхним пределом
- •Формула Ньютона-Лейбница.
- •39. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства). Несобственные интегралы с бесконечными пределами интегрирования
- •40. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
- •41. Понятие о дифференциальном уравнении. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса.
- •Задача о построении математической модели демографического процесса. Задача Коши
- •42. Простейшие дифференциальные уравнения 1-го порядка (разрешенные относительно производной, с разделяющимися переменными) и их решение. Примеры.
- •Рассмотрим некоторые типы дифференциальных уравнений 1-го порядка.
- •Неполные дифференциальные уравнения 1-порядка.
- •Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
- •43. Однородные и линейные дифференциальные уравнения 1-го порядка и их решения. Примеры. Однородные дифференциальные уравнения 1-го порядка.
- •Линейные дифференциальные уравнения 1-го порядка.
- •44. Определение числового ряда. Сходимость числового ряда. Необходимый признак сходимости рядов (доказать). Примеры.
- •Понятие числового ряда. Сходимость ряда и его сумма
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •45. Гармонический ряд и его расходимость (доказать). Расходимость гармонического ряда
- •46. Признаки сравнения и Даламбера сходимости знакоположительных рядов. Примеры. Достаточные признаки сходимости ряда с положительными членами
- •47. Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов. Абсолютная и условная сходимость рядов.
- •Знакопеременные ряды
- •Свойства степенных рядов
- •Ряд Маклорена
30. Общая схема исследования функций и построения их графиков. Пример.
Общая схема исследования функции и построения ее графика.
Найти область определения .
Исследовать функцию на четность – нечетность.
Найти вертикальные асимптоты и точки разрыва (если есть).
Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).
Найти экстремумы и интервалы монотонности функции.
Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.
Схематично построить график.
Подробная схема исследования функции и построения графика.
Найти область определения .
Если у есть знаменатель, он не должен обращаться в 0.
Подкоренное выражение корня четной степени должно быть неотрицательным (больше либо равно нулю).
Подлогарифмическое выражение должно быть положительным.
Исследовать функцию на четность – нечетность.
Если
 ,
то функция четная.
,
то функция четная.Если
 ,
то функция нечетная.
,
то функция нечетная.Если не выполнено ни , ни , то – функция общего вида.
Найти вертикальные асимптоты и точки разрыва (если есть).
Вертикальная асимптота может возникнуть только на границе области определения функции.
Если
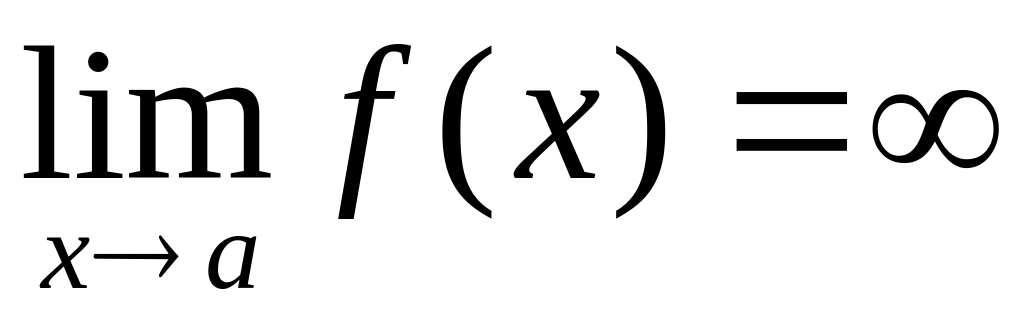 (
( или
или
 ),
то
),
то
 – вертикальная асимптота графика
.
– вертикальная асимптота графика
.
Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).
Если
 ,
то
,
то
 – горизонтальная асимптота графика
.
– горизонтальная асимптота графика
.Если
 и
и
 ,
то прямая
,
то прямая
 является наклонной асимптотой графика
.
является наклонной асимптотой графика
.Если пределы, указанные в п. a, b, существуют только при одностороннем стремлении к бесконечности (
 или
или
 ),
то полученные асимптоты будут
односторонними: левосторонними при
и правосторонними при
.
),
то полученные асимптоты будут
односторонними: левосторонними при
и правосторонними при
.
Найти экстремумы и интервалы монотонности функции.
Найти производную .
Найти критические точки (те точки, где или где не существует).
На числовой оси отметить область определения и ее критические точки.
На каждом из полученных числовых интервалов определить знак производной .
По знакам производной сделать вывод о наличии экстремумов у и их типе.
Найти экстремальные значения .
По знакам производной сделать вывод о возрастании и убывании .
Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.
Для того, чтобы найти точки пересечения графика с осью , надо решить уравнение
 .
Точки
.
Точки
 ,
где
,
где
 – нули
,
будут точками пересечения графика
с осью
.
– нули
,
будут точками пересечения графика
с осью
.Точка пересечения графика с осью
 имеет вид
имеет вид
 .
Она существует, только если точка
.
Она существует, только если точка
 входит в область определения функции
.
входит в область определения функции
.
Схематично построить график.
Построить систему координат и асимптоты.
Отметить экстремальные точки.
Отметить точки пересечения графика с осями координат.
Схематично построить график так, чтобы он проходил через отмеченные точки и приближался к асимптотам.
Пример.
Исследовать функцию
![]() и схематично построить ее график.
и схематично построить ее график.
1.![]() .
.
2. – функция общего вида.
3.
Поскольку
![]() и
и
![]() ,
то прямые
,
то прямые
![]() и
являются вертикальными асимптотами;
точки
и
являются точками разрыва.
и
являются вертикальными асимптотами;
точки
и
являются точками разрыва.
4

![]() ,
прямая
,
прямая
![]() – горизонтальная асимптота графика
.
– горизонтальная асимптота графика
.
5.
![]() ;
при
.
На числовой оси отмечаем точки
,
(не входят в область определения
)
и
(критическая точка
).
На каждом из полученных числовых
интервалов определяем знак производной
:
при
;
при
.
На числовой оси отмечаем точки
,
(не входят в область определения
)
и
(критическая точка
).
На каждом из полученных числовых
интервалов определяем знак производной
:
при
![]() ,
при
,
при
![]() ,
при
,
при
![]() ,
при
,
при
![]() .
Делаем выводы:
– точка максимума (в этой точке производная
меняет знак с «+» на «–»),
.
Делаем выводы:
– точка максимума (в этой точке производная
меняет знак с «+» на «–»),
![]() ;
при
;
при
![]() и при
и при
![]() возрастает; при
возрастает; при
![]() и при
и при
![]() убывает.
убывает.
6.
Точка пересечения графика
с осью
:![]() .
Точка пересечения графика
с осью
отсутствует, так как точка
не входит в область определения функции
.
.
Точка пересечения графика
с осью
отсутствует, так как точка
не входит в область определения функции
.
7. См. рис. 7.
