2.1.5. Задержка и искажение импульсов на связях.

 

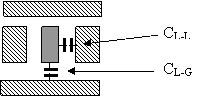
С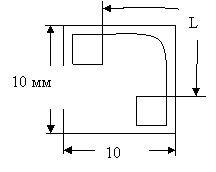 оединительная шина между двумя блоками ИС.

 

 

 

 

 

 

 

Длина связи может достигать 1 см.

 

Важнейшая характеристика связи – длительность времени, в течение которой импульс (или фронт импульса) пробегает вдоль связи. Эта длительность определяется длиной связи и скоростью распространения электромагнитной волны вдоль линии передачи, образованной связью.

 

 ,

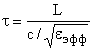где с – скорость света, _эфф – эффективная диэлектрическая проницаемость материала окружающего линию связи, L – длина связи.

Рассмотрим две модели соединительной шины в составе ИС.

 

1)       Случай, когда импульс, несущий информацию, длиннее времени пробега по связи.

_имп > ,

где _имп - длительность импульса.

В этом случае шина может рассматриваться как RC цепь, а задержка сигнала определяется временам заряда ёмкости С через сопротивление R. Очевидно, что это время пропорционально квадрату длины связи, так как и ёмкость связи и её сопротивление пропорциональны длине.

 

2)      Случай, когда импульс короче времени пробега по связи.

 

_имп < .

В этом случае шину следует рассматривать как RLC линию передачи, и тогда практически все вопросы задержки и искажения импульсных сигналов смыкаются с вопросами передачи сигналов по линиям связи, которые решаются техникой сверхвысоких частот (СВЧ).

 

 

 

 

 

1) Задержка цифрового сигнала на связях

(RC – МОДЕЛЬ)

	R1
			C1

   

 

 

Здесь R₁ – погонное сопротивление шины, С₁ – погонная ёмкость шины.

 

            ,                                                          

 

где  - проводимость материала шины (для меди при Т = 300 К  = 610⁷ 1/Омм)

      w, h – ширина и толщина шины.

Чем меньше размеры транзисторов, тем меньше приходится делать и размеры поперечного сечения шин, обеспечивающих связи между транзисторами. Положим, что приближённо

                                                wh  l ²

где l – характерная длина (длина канала для МДП транзистора)

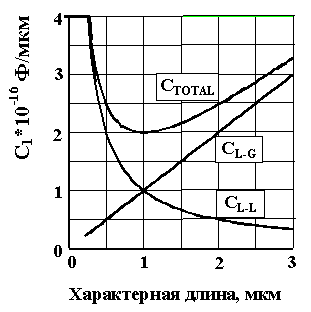
В случае многослойного расположения связей погонная ёмкость определяется как ёмкостью шины на разделяющий экран (C_L-G, ground plane) так и на элементы конструкции, расположенных рядом с шиной (C_L-L).

 

 

 

 

 

 

 

 

Дальнейшие оценки задержки цифрового сигнала (импульсов) на RC связях основаны на обзорной статье:

R.Y. Havemann, J.A. Hutchdy, “High-Performance Interconnections: An Integration Overview”, Proc. IEEE, Vol. 89, No. 5, pp. 586-601 (May 2001)

 

Расчёт погонной ёмкости для диэлектрической проницаемости материала изолирующих слоёв _д  15 приводит к зависимости погонной ёмкости от характерного размера элемента интегральной схемы, который представлен на рисунке. Можно ориентировочно считать, что для интегральных схем с достаточно высоким уровнем интеграции (l = 0,25 – 1,0 мкм)

 

С⁰₁ = 2.510^-16 Ф/мкм.

 

 

 

 

 

            Теперь можем оценить величину постоянной времени перезарядки шины длиной L.

_св = RC = R₁C₁L²,

 

где R и C полное сопротивление и полная ёмкость шины, R₁ и C₁ – её погонные параметры. Собирая вместе сделанные выше оценки, получим:

 

                                                  ()

 

Для сравнения приведём оценку задержки импульсного сигнала в транзисторе:

 

 ,                                                          ()

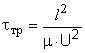где  - подвижность, U – рабочее напряжение транзистора.

 

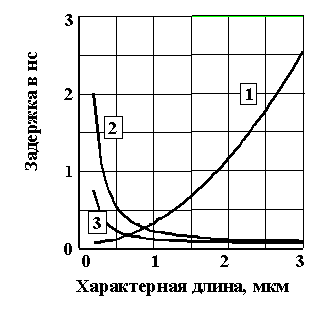
            На рисунке приведены зависимости времени задержки в транзисторе         ( кривая 1) и на связях (кривые 2 и 3) в функции от характерного размера для

 = 610⁷ 1/Омм,   = 0,004 м²/Вс,  U = 1 В,  L = 5 мм (кривая 2)  и  L = 3 мм (кривая 3).

            Приведённые оценки показывают, что при L = 3 - 5 мм для транзисторов с длиной канала меньше 0,5 мкм задержка на связях оказывается большей, чем задержка на одном транзисторе. Заметим, что логические схемы содержат больше одного транзистора на одну логическую операцию, поэтому задержка на одну логическую операцию оказывается больше, чем на один транзистор. Поэтому стремление ещё больше уменьшить задержку на один транзистор оправдано, то есть оправдано сокращение длины канала, и оправдана разработка транзисторов с длиной канала менее четверти микрометра. 

 

 

Суммарная задержка определяет допустимую тактовую частоту, с которой производятся вычислительные операции в ИС. Для ориентировочной оценки можно использовать простое соотношение между тактовой частотой и суммарной задержкой сигнала:

                                                      ()

 

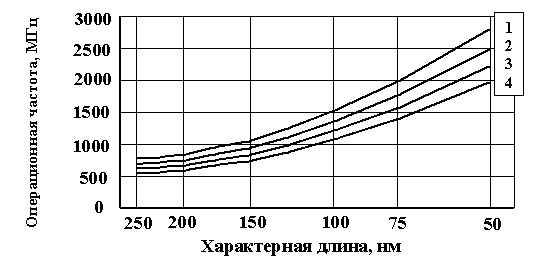
            На следующем рисунке приведена зависимость тактовой частоты от характерного размера активного элемента ИС.

Построенные на рисунке кривые отвечают следующим параметрам цепей связи в ИС:

1)      Связи образованы плёночными проводниками из меди, изолирующие прослойки выполнены из полимерных материалов с диэлектрической проницаемостью прядка 2,

2)      Связи образованы плёночными проводниками из алюминия, изолирующие прослойки выполнены из полимерных материалов с диэлектрической проницаемостью прядка 2,

3)      Связи образованы плёночными проводниками из меди, изолирующие прослойки выполнены из оксидов с диэлектрической проницаемостью прядка 15,

4)      Связи образованы плёночными проводниками из алюминия, изолирующие прослойки выполнены из оксидов с диэлектрической проницаемостью прядка 15.