Лекция 4, 5 Электропроводность полупроводниковых материалов

1. Общие сведения о электропроводности полупроводников

2. Статистика носителей заряда

1 Общие сведения о электропроводности полупроводников

Выражение для электропроводности полупроводника в общем случае может быть записано в виде:

, (1.2.1)

где е_i, n_i, _i - соответственно заряд, концентрация и подвижность носителей заряда; индекс “i” относится к типу носителей заряда (электроны и дырки). Если в электропроводности участвуют один тип электронов и один тип дырок, то:

. (1.2.2)

Для собственного полупроводника, где соблюдается условие n=p=n_i получим:

. . (1.2.3)

В случае полупроводника n-типа (n_n>>p_n) или p-типа (p_p>>n_p) проводимость может быть представлена следующими выражениями:

. (1.2.4)

Нетрудно увидеть, что величина электропроводности полупроводника зависит от внешних условий (температуры, освещенности, силовых полей и т. д.) и внутренних характеристик материала (зонная энергетическая структура, уровень легирования примесями, дефектность кристаллической решетки и т. д.), т.е. от тех факторов, которые определяют величину концентрации и подвижности носителей заряда.

2 Статистика носителей заряда

2.1. Концентрация носителей заряда в полупроводниках

2.1.1 Собственные полупроводники

В соответствии с (1.2.7) и (1.1.27) концентрация равновесных электронов n₀ и дырок p₀ соответственно в зоне проводимости и валентной зоне можно определить как

(1.2.8)

и

, (1.2.9)

где N_ЗП и N_ВЗ – соответственно плотность состояний в зоне проводимости и в валентной зоне.

В приближении квазисвободных носителей заряда (параболическое приближение) для оценки концентраций электронов и дырок можно получить простые аналитические выражения:

(1.2.10)

и

, (1.2.11)

где N_C и N_V - эффективные плотности состояний вблизи дна зоны проводимости W_C и потолка валентной зоны W_V (или концентрации вырождения), соответственно определяемые как

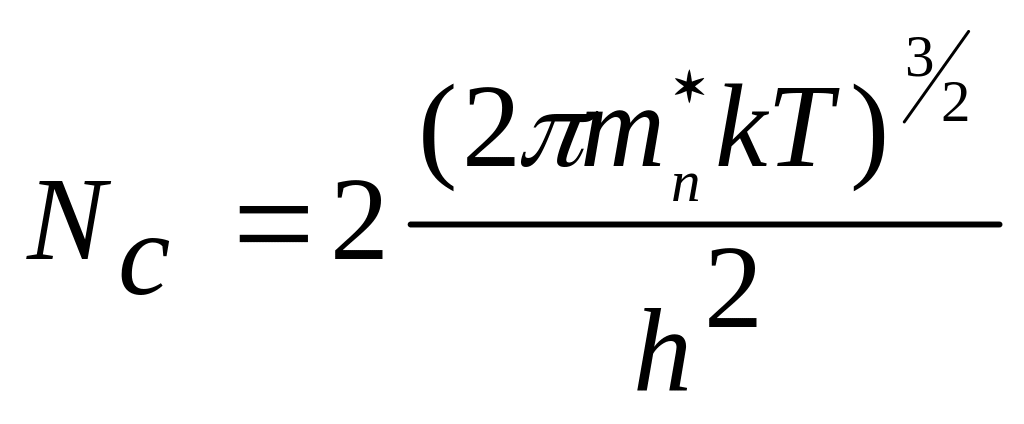, (1.2.12)

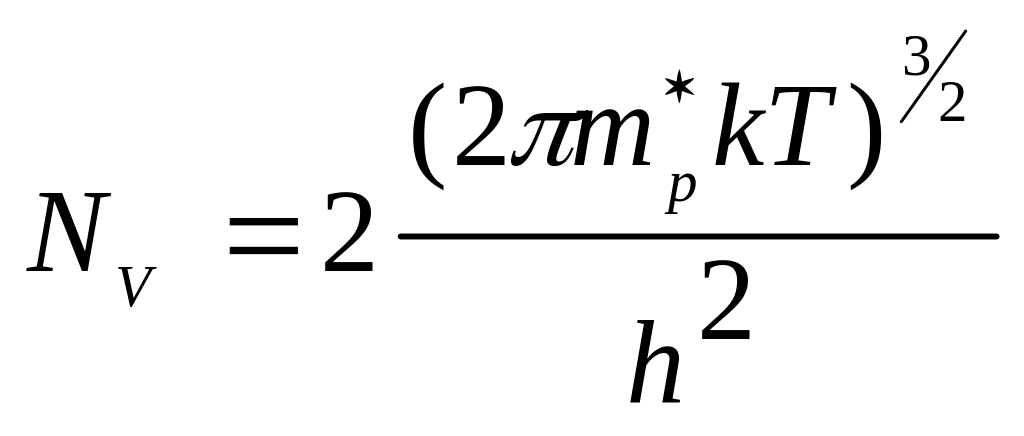, (1.2.13)

а и -эффективные массы электронов и дырок, соответственно вблизи дна зоны проводимости и валентной зоны.

В собственном полупроводнике справедливо соотношение п₀=р₀=n_i. Используя выражения (1.2.10) и (1.2.11) несложно получить расчетное соотношение для оценки собственной концентрации носителей заряда

(1.2.14)

откуда

. (1.2.15)

Концентрация электронов и дырок в собственном полупроводнике оказывается независимой от положения уровня Ферми и растет с температурой по экспоненциальному закону с энергией активации . Это понятно, если учесть, что энергия W_g затрачивается на создание пары носителей: электрона и дырки, а соответственно на каждый из носителей в этой паре приходится энергия в два раза меньшая.

2.1.2 Примесные полупроводники

Концентрации основных носителей заряда в примесных полупроводниках может быть оценена из соотношений (1.2.10) и (1.2.11). Однако, если известна концентрация и энергия ионизации атомов донора и акцептора, то концентрацию электронов и дырок удобно рассчитывать по следующим формулам

, для n – типа (1.2.16)

, для р – типа, (1.2.17)

где - соответственно энергии ионизации атома донора и атома акцептора; N_d, N_A - соответственно концентрация ионизированных доноров и акцепторов.

Учитывая, что произведение концентрации электронов и дырок есть величина постоянная для данного полупроводника при заданной температуре и давлении (закон действующих масс), концентрацию неосновных носителей заряда можно оценить, используя этот закон

(1.2.18)

, (1.2.19)

где - сответственно концентрация неосновных носителей заряда.

Компенсированные полупроводники. Полупроводник , в котором концентрация ионизированных акцепторов равна концентрации ионизированных доноров , называется компенсированным.

Такие полупроводники ведут себя, как собственные и для них следует пользоваться теми же соотношениями по оценке концентрации носителей заряда. Если концентрации ионизированных акцепторов и доноров не совпадает, то такой полупроводник ведет себя, как примесный р - типа или n – типа соответственно при  или  . В данном случае следует пользоваться статистикой носителей заряда принятой для примесных полупроводников. При этом концентрация активной ( нескомпенсиррованной ) примеси определяется как

N_d= - ( n – типа) (1.2.20)

N_a= - ( p – типа) (1.2.21)

При оценке концентрации носителей заряда в полупроводниках независимо от их типа удобно пользоваться соотношениями выражающими закон электронетральности, суть которого заключается в том, что в нейтральном образце суммарная концентрация положительно заряженных подвижных и неподвижных носителей заряда, должна равняться таковой для отрицательных зарядов. В частности, ниже представлены соотношения, которые выражают условие электронейтральности в полупроводниках различного типа:

(собственный, компенсированный )

(n – типа) (1.2.22)

(р – типа) (1.2.23)

(частично компенсированный р – типа) (1.2.24)

(частично компенсированный n – типа) (1.2.25)