3. Типовая схема фрактального сжатия

С учётом вышесказанного, схема компрессии выглядит так: изображение R разбивают на кусочки r_i, называемые ранговыми областями. Далее для каждой области r_i находят область d_i и преобразование w_i такие, что выполняются следующие условия:

1. d_i по размерам больше r_i.

2. w_i (r_i) имеет ту же форму, размеры и положение, что и r_i.

3. Коэффициент u преобразования w_i должен быть меньше единицы.

4. Значение должно быть как можно меньше.

Первые три условия означают, что отображение w_i будет сжимающим. А в силу четвёртого условия кодируемое изображение R и его образ W (R) будут похожи друг на друга. В идеале R = W (R). А это означает, что наше изображение R и будет являться неподвижной точкой W. Именно здесь используется подобие различных частей изображения (отсюда и название – «фрактальная компрессия»). Как оказалось, практически все реальные изображения содержат такие похожие друг на друга, с точностью до аффинного преобразования, части.

Таким образом, для компрессии изображения W нужно:

1. Разбить изображение на ранговые области r_i (непересекающиеся области, покрывающие все изображение).

2. Для каждой ранговой области r_i найти область d_i (называемую доменной), и отображение w_i, с указанными выше свойствами.

3. Запомнить коэффициенты аффинных преобразований W, положения доменных областей d_i, а также разбиение изображения на домены.

Соответственно, для декомпрессии изображения нужно будет:

1. Создать какое-то (любое) начальное изображение R₀.

2. Многократно применить к нему отображение W (объединение w_i).

3. Так как отображение W сжимающее, то в результате, после достаточного количества итераций, изображение придёт к аттрактору и перестанет меняться. Аттрактор и является нашим исходным изображением. Декомпрессия завершена.

Именно это и позволяет при развертывании увеличивать его в несколько раз. Особенно впечатляют примеры, в которых при увеличении изображений природных объектов проявляются новые детали, действительно этим объектам присущие (например, когда при увеличении фотографии скалы она приобретает новые, более мелкие неровности).

4. Оценка коэффициента сжатия и вычислительных затрат

Размер данных для полного определения ранговой области рассчитывается по формуле:

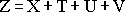
(10)

где X – количество бит, необходимых для хранения координат нижнего левого угла домена, T – количество бит, необходимых для хранения типа аффинного преобразования, U и V – для хранения коэффициентов контраста и яркости.

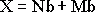
(11)

где Nb и Mb – количество бит, необходимых для хранения каждой из координат, рассчитываются по следующим формулам:

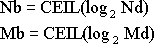
(12)

Здесь CEIL – функция округления до максимального целого, Md и Nd – количество доменов, умещающихся по горизонтали и вертикали, которые рассчитываются по формулам:

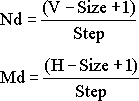
(13)

где V и H – вертикальный и горизонтальный размеры изображения, Size – размер доменного блока, Step – шаг поиска доменной области.

Для хранения преобразования T необходимо 3 бита.

Для хранения U и V необходимо 9 и 7 бит соответственно.

Для примера возьмём изображение размером 256x256 пикселей, и будем исследовать доменную область с шагом 4 пикселя.

Nd = Md = (256 - 8 + 1) / 4 = 62

Nb = Mb = CEIL (log₂ 62) = 6

Х = 12

Z = 12 + 3 + 6 + 6 = 27

Коэффициент сжатия S составляет

S = (8 * 8 * 8) / 27 = 19

Коэффициент сжатия не так велик, как хотелось бы, но и параметры сжатия далеко не оптимальны, и коэффициент может увеличиваться в разы.

А теперь оценим вычислительную сложность данного алгоритма. На этапе компрессии мы должны перебрать все доменные области – 1'024 штуки, для каждой – все ранговые – 58'081 штука (при шаге 1), а для каждой из них, в свою очередь, – все 8 преобразований. Итого получается 1'024 х 58'081 х 8 = 475'799'552 действия. При этом эти действия не тривиальны и включают несколько матричных операций, которые, в свою очередь, включают операции умножения и деления чисел с плавающей точкой.

К сожалению, даже на современном ПК (а именно для таких машин хотелось реализовать алгоритм) понадобится недопустимо много времени для того, чтобы сжать изображение размером всего 256 х 256 пикселов. Очевидно, что рассмотренный алгоритм нуждается в оптимизации.