45(2) Спиновые волновые функции:

Опер-ры спина в представл.имеют вид: .

Н айдём собств. ф-ции операторов Ŝ_X, Ŝ_Y, Ŝ_Z: где χ – собств.функция. χ_ms – нумир. квант. числом m_S; χ_ms(S_Z) – собственная функция оператора спина Ŝ_X χ_ms(S_Z)= m_S ћ χ_ms.

При m_S=1/2: при m_S=–1/2: - это спиновые ф-ции.

Наличие спина приводит к дополнительной степени свободы, т.к. Эл-он может находиться в состояниях с различными значениями проекции спина.

С учётом спина волновая ф-ция примет вид: ψ(x, y, z, ћ/2, t) или ψ(P_X, P_Y, P_Z, S_Z, t). Волновая ф-ция должна записываться в виде столбца.

Введём преобразование: ψ(x, y, z, ћ/2, t)= ψ₁(x, y, z, t), и ψ(x, y, z,-ћ/2, t)= ψ₂(x, y, z, t)

Действие  спин-го оператора на такую функцию имеет след-ую структуру:

, где

46. Свойство атомизма : Рассмотрим систему из произв. числа одинаковых микрочастиц (одного сорта). основное св-во частиц одного сорта – одинаковость их врождённых физ. признаков (качеств, не зависящих от состояния ч-цы – эл.заряд, масса покоя, спин). Эта строгая одинаковость врождённых признаков – свойство атомизма. Это св-во не имеет аналогов в макромире (не  2ух строго идентичных предметов). Св-во атомизма приводит к проблеме различия частиц в системе одного сорта. Мыслительно  2 способа разделения: 1) по врождённым физическим признакам, 2) по состоянию (напр: местоположению). Но эти способы пригодны только на макроуровне. 1ый способ не работает из-за св-ва атомизма, а 2ой из-за соот-ношения неопределённостей (координаты определяются с точностью до _L или _x, т.е следить за траекторией можно с точностью до _x)

Принцип тождественности.микрочастиц :

микроч-цы одного сорта в системе этих частиц становятся неразличимыми

Т.о описать в такой сист. отдельную ч-цу невозможноописывается лишь состояние системы в целом. Это состояние задаётся волн. функцией ψ(q₁, q₁,…q_N,t) (1), q_i=(x_i , y_i, z_i, S_zi) – полный набор переменных для одной ч-цы. Из принципа тожд., что поменяв местами q_i и q_j в (1)получим то же самое состояние с-мы (физически исходн. и новое состояния неразличимы).

Сформулируем ещё один принцип тожд-ти микрочастиц: в системе одинаковых микроч-ич реализуются только те состояния системы, которые не изменяются при обмене 2ух частиц.

Симм. и антисимм. состояния.

Из принц. тожд-ти , волн. функция ψ(q₁, q₁,…q_N,t) системы N одинаковых ч-иц должна быть такой, что при обмене 2ух частиц (q_i и q_j местами) новое состояние физически не отличалось от исх-го.

Обозначим ψ(q₁, q₁,…q_N,t) через ψ(ik), обратная ф-ция путём обмена - ψ(ki), введём оператор перестановки i и k частиц: и .

Эти две функции могут различаться только постоянным множителем: . Подействовав оператором перестановки, получим:  =±1. Т.о =1 – соотв-ет симметричной (относит. перестановки i и k частиц) волновой функции системы. = –1 – соотв-ет антисимметричной -//-.

Вид симметрии волновых функций не меняется с течением времени.

Если волновая функция, описывающая состояние системы, в какой-либо момент времени является симметричной (антисимметричной), то этот тип симметрии сохраняется и в любой другой момент времени.

Бозе-частицы (с целым спином): ч-цы, состояния кот-ых описываются симметр-ми волн. функ-ми, наз-ся бозе-частицами или бозонами. (подчиняются стат-ке Бозе-Эйншт).

l_S =0,1 - скалярн. и вект.меезоны (π⁺, π ^–, π⁰), l_S =2 – гипотетич. гравитоны, l_S =1 – фотон.

Ферми-частицы (с полуцелым спином): ч-цы, состояния кот-ых описываются антисимметр. волн. ф-ми, наз-ся ферми-частицами или фермионами. (подчиняются стат-ке Ферми-Дир).

l_S =1/2 – протон, нейтрон, μ- мезон, ν, кварки, электрон, l_S =3/2 –Ω^– - гиперон.

Связь между спином частиц, образующих квантовую систему, и типом статистики была установлена Паули. Является ли сложная частица бозоном или фермионом, зависит от того, каков результирующий спин этой частицы.

Принцип запрета Паули: Рассмотрим систему из 2ух одинаковых фермионов. Волн. ф-ция ψ(q₁, q₂,t) (1). q₁ и q₂ – полный набор переменных. Эта ф-ция симметрична отн-но перестановки частиц:

ψ(q₁, q₂,t)= –ψ(q₁, q₂,t) (2). Обозначим через n₁ и n₂ – полные наборы кв. чисел. Каждый набор состоит из 4ёх кв-ых чисел ψ_n1(q₁), ψ_n2(q₂). Совокупность ψ_n1(q₁) образует полную систему ф-ций в простр-ве q₁, аналог. ψ_n2(q₂). В простр-ве переменных q₁ и q₂, в качестве полной системы базисных функций могут служить произ-ведение вида: ψ_n1(q₁)·ψ_n2(q₂). (1)разложим в ряд:

(3)

поменяем ч-цы местами, (5)

сравниваем (3)и(5) и учит.(2)С(n₂, n₁, t)= –С(n₁, n₂, t) (6); - вероятность того, что при одновременном измерении обоих состояний фермионов в системе, один будет обнаружен в состоянии, характеризующимся набором чисел n₁, а второй – набором чисел n₂.

Положим n₂.= n₁ =n в (6)|C(n, n, t)|² – вероятность того, что при одновременном измерении обеих фермионов, каждый будет обнаружен в кв. состоянии хар-ся одним и тем же набором квантовых чисел и эта вероятность : W_n,n=0, |C(n, n, t)|² = 0- при одновременном сум-ии сост-й 2-х фермионов в системе невозможно получить 1 результат изм-ия.

Принцип запрета Паули

в системе тождественных фермионов не может быть двух частиц, находящихся в одном и том же квантовом состоянии.

47. Периодический закон Менделеева: (1869)Суть: расположив хим. элементы в порядке атомного веса, он обнаружил ярко выраж-ую периодичность хим. св-в элементов. Но в некоторых местах М. переставил эл-ты, чтобы не нарушать периодичность. После установления в опытах Резерфорда ядерной модели атома, было обнаружено, что хим.эл-ты таблицы М. расположены в порядке возрастания заряда Z_e (Z – число протонов). После этого открытия перестановки были объяснены.

Но ни откр-ия Резерф, ни теория Бора не объясняли период.законы. Это объяснялось тем, что атом – кв-мех. система и законам кв.мех-ки подчин-ся больш-во его св-в.

Положения кв.мех-ки для объяснения периодического закона:

1) кв-мех расчёт энергетический уровней; 2) принцип min энергии; 3) принцип запрета Паули;

Квантовое расщепление эн.уровней позволило определить взаимное расположение оболочек и подоболочек атома на энергет диаграмме.

Принц. min энергии и пр.запрета Паули определил порядок заполн. эн.уровней, оболочек, подоболочек e^–ми

2 – при данном общем числе электронов в атоме реализуется состояние, соответствующее min энергии.

3 – в одном кв. сост-ии не может нах-ся более 1 электрона.

Идеальная схема: Рассмотрим упрощённую модель атома – эл-ны не в/д др. с др. Состояние каждого эл-на рассчитывается, так, как будто нет других электронов. Хорошими кв-ми числами являются n, l, m, m_s.

Энергия E_n,l зависит от 2ух квант.чисел, поэтому вводят оболочки и подоболочки.

Оболочку составл. эл-ны в сост с одним значением n.Подоболочку – эл-ны, наход. в сост-ии с одним знач l

Max возможное число эл-ов в оболочке и подоболочке = числу различных кв.сост., соотв-их обол. и подобол.

2(2l+1) – в обол=ке при n-фиксир.; 2n² – в подобол-ке при l-фиксир.

Оболочки обозначают: K(n=1) L(n=2) M(n=3) N(n=4) O(n=5)

Подоболочки обознач: s(l=0) p(l=1) d(l=2) f(l=3) g(l=4 ) (См. табл)

Кв-мех расчёт энергет уровней микроч-цы, нах-ся в центр-симм поле даёт монотонное возрастание зав-ти E от n и l в упрощённой модели оболочки и подоболочки не будут перекрываться .

Строение внешней оболочки, на которой есть эл-ны, периодически повторяется. Химич. свойства определ-ся строением внешней оболочки периодич. повторение хим-их св-в элементов, расположенных в порядке возрастания заряда их ядра. Рассм-ое грубое приближение объясняет качественно период. закон – периодич-ность хим. св-в.

С классич. т.зр. идеальная схема имеет расхождения с реальной периодичностью: в класс.период: 2,8,18,32,50.. в реальн.период: 2,8,8,18,18,32. Это объясн-ся не учтённым в/д между электр-ми.

О 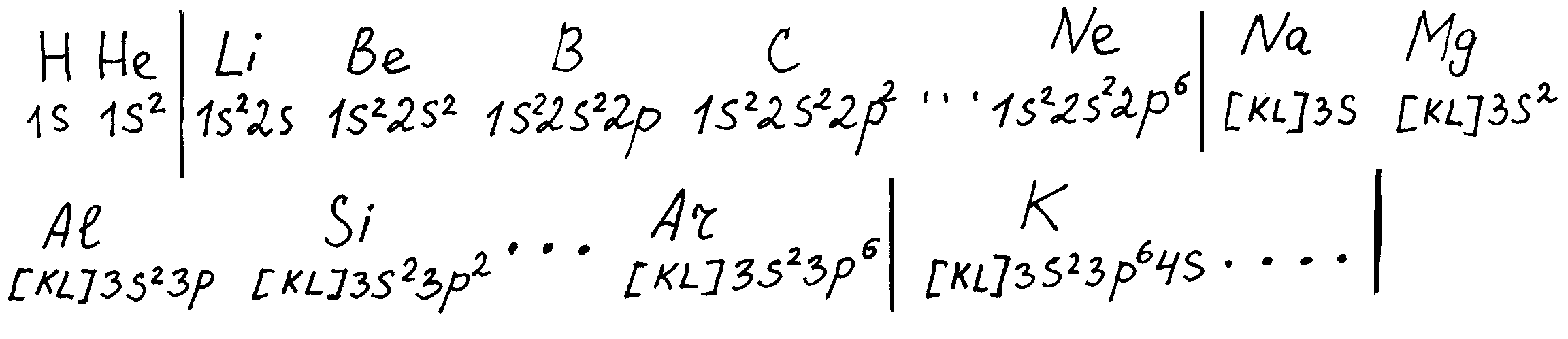тличие реальной картины от идеальной: При малом числе электр. в/д не играет роли. Различия в схемах появляются с 3-го периода, т.к. учёт в/д между электронами приводит к нарушению монотонного возрастания зависимости E от n и l, соседние оболочки и подоболочки начинают перекрываться (в энергетич. смысле) заполнение происходит след.образом:

предыдущая оболочка не заполнена, а уже заполняются следующие – начинается новый период.

Лантаноиды: Элемент La (Лантан) №57, конфиг. 6s². У La незаполненной до конца явл-ся не только 5ая, но и 4ая оболочка, строение которой на хим. св-ва практ. не влияет. У всех этих элементов практически одинаковые хим. св-ва. Все эти эл-ты вынесены за пределы таблицы и наз лантаноидами.

Актиноиды: Элемент Ac (Актиний) №89 (VII пер), конфиг. 7s². У La незаполненны до конца 6ая и 7ая оболочки. Все эти эл-ты схожи по свойствам и наз актиноидами.

Трансурановые эл-ты: По мере возрастания порядкового номера ядро становится нестабильным. С 93 номера начинаются нестабильные элементы - трансурановые элементы

Периодическая таблица, вследствие нестабильности эл-ов, имеет естественный конец. На К нарушается заполнение оболочек (вместо 3d начинается заполнение 4s)

48. Протонно-нейтронная модель: В 1932 году русский физик Иваненко и немецкий физик Гейзенберг независимо друг от друга предложили протонно-нейтронную модель ядра. Согласно этой модели, атомное ядро состоит из протонов и нейтронов. Ядерные частицы получили название - нуклоны. Так как массы протона и нейтрона мало отличаются друг от друга и равны 1а.е.м., то массовое число А определяет общее число нуклонов в ядре. Число протонов в ядре, очевидно, равно зарядовому числу (Z). Тогда число нейтронов N=A-Z. Протон: обозначается «p», открыт Резерфордом 1919г. масса:m_p=1836,2 m_e ~1,672*10^-27 кг, энергия покоя: m_pc ~ 338,256 МэВ, заряд: q_p=e=1,602*10^-19 Кл, спин: S_z = +- 1/2 - фермион, магнитный момент: , где - ядерный магнетон, время жизни: лет, радиус: м. Нейтрон: обозначается «n», открыт Чедвигом в 1932г. m_n=1,675*10^-27 кг, m_nc ~ 935,55 МэВ, |q_p| <e*10^-21, S_z = +- ½ - фермион, , . Нуклон: В 1932г. Гейзенберг предположил, что n и p – два состояния одной и той же частицы. В 1939г. по этому поводу Белинфанте предложил «нуклон». Для того чтобы различать n и p, придумали квантовое число «изоспин» [Т], наз потому, что весь матем аппарат со спина перенесли на изоспины: , для p – «+», а для n – «-». Для системы из двух нуклонов полный изоспин может принимать значения 1 или 0. Барионный заряд(В)- вспомогательное число, сохраняющееся в определенном классе превращений элементарных частиц. Для нуклонов В=1, для электрона В=0, для ядра В=А. Электрический заряд(q) - количественная характеристика, показывающая степень возможного участия тела в электромагнитных взаимодействиях. Единица измерения заряда в СИ — кулон. Носителями электрического заряда являются электрически заряженные элементарные частицы. Для нуклона заряд изопина и барион заряд связаны следующим образом: . Изоспины частиц могут принимать значения 0, 1/2, 1, 3/2. Для ядра: . Закон сохранения барионного заряда: барионный заряд приблизительно сохраняется во всех взаимодействиях стандартной модели(теоретическая конструкция, описывающая электромагнитное, слабое и сильное взаимодействие всех элементарных частиц). Закон сохранения электрического заряда: Электрический заряд замкнутой системы сохраняется во времени и квантуется - изменяется порциями, кратными элементарному электрическому заряду. - ядро. Нуклиды: совокупность ядер, идентичных по своему составу (у них A или N или Z). Изотопы: одинаковое Z ( ). Изобары: одинаковое А ( ). Стабильные изотопы - ядра атомов которых не подвержены самопроизвольному превращению в другие ядра с испусканием различных частиц. Магические ядра: атомные ядра, содержащие 2, 8, 20, 28, 50, 82, 126 протонов или нейтронов (числа 2, 8 и т.д. называются магическими).Они отличаются от соседних ядер повышенной устойчивостью, большей распространённостью в природе и некоторыми другими особенностями. Дважды магические: В том случае, когда и N и Z равно магическому числу. Дефект массы – разность между массой нуклонов, составляющих ядро и массой самого ядра: . Энергия связи – энергия, необходимая для полного разделения ядра атома на отдельные нуклоны: . Удельная энергия связи: энергия связи, приходящаяся на один нуклон ядра: . Примерные графики зависимости: В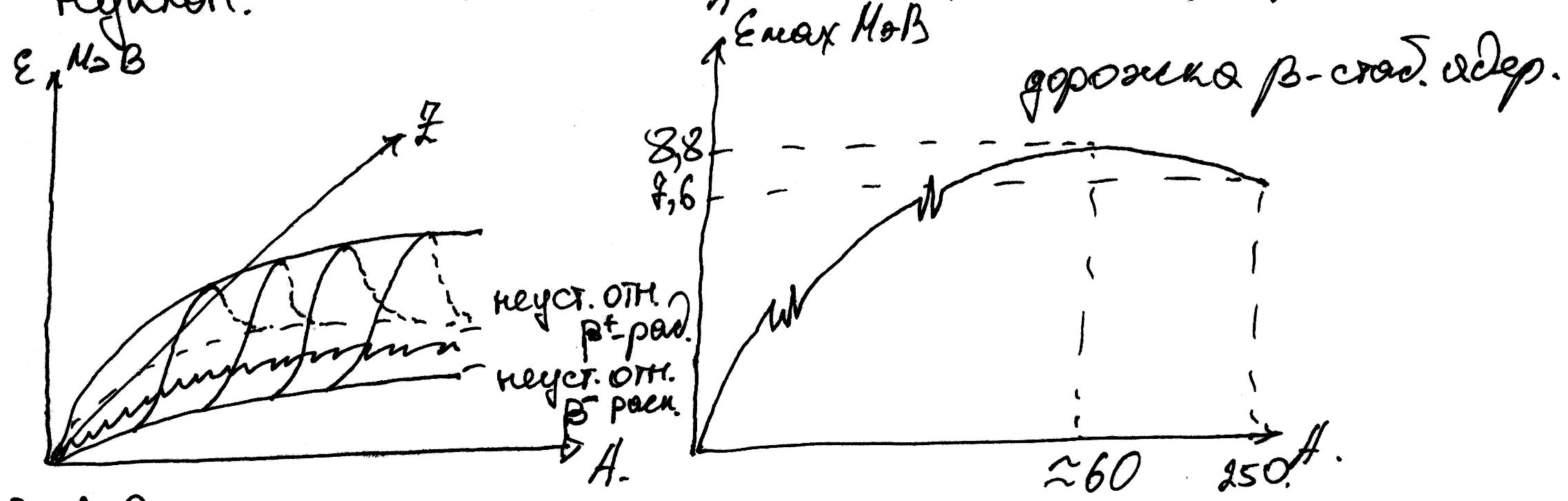 ыводы: 1) Ядра легких элементов, способны синтезироваться в более тяжелые ядра, обладают большей удельной энергией, т.е. предпочтительной является реакция для образования ядер с большей удел энерг (термоядерный синтез); 2)Ядра тяж эл-тов, предрасположены к делению на ядра средней части таблицы;

3) Чет-чет яжра обладают большей удел энерг; 4)нечет-нечет обладают меньшей удел энерг; 5) Особой стабильностью обладают ядра, число нуклонов которых совпадает с магическим рядом. Полуэмпирическая формула Вайцзеккера: . Физический смысл слогаемых: - краевой эффект – у крайних нуклонов в ядре соседей меньше, чем у внутр; - обусловлен кулоновским притяжением протонов; - обусловлен тем, что ядро с равным числом протонов и нейтронов обладает большей энерг связи, чем остальные ядра. (чет-чет – обусловлен тем, что чет-чет ядро) или = 0 (нечет-чет – обладают большей энерг связи, чем неч-неч)

или = (неч-неч). Спин и проекция спина: известно, что е и p обладают спином = 1/2 в единицах :

48(2)…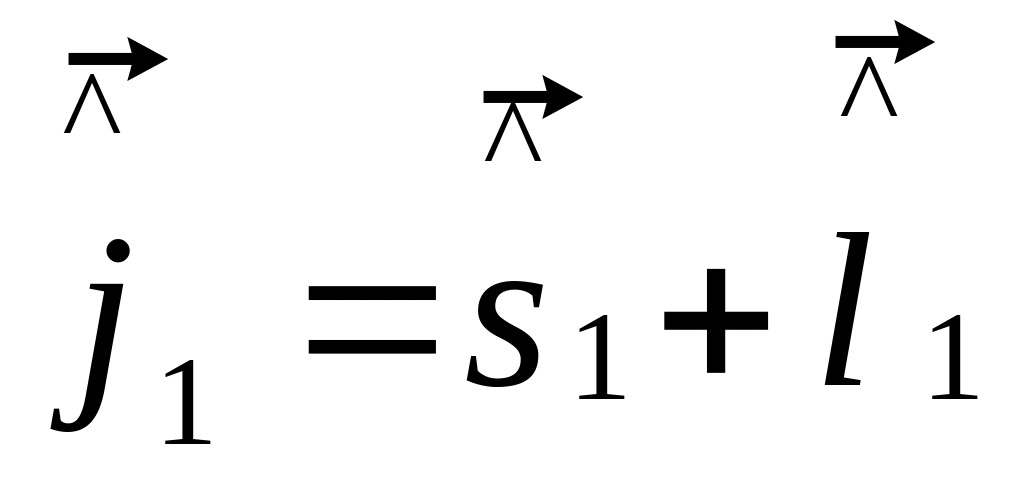 , где , l=0,1,2,.. , аналог и для S и L. , где -спин ядра, -сум сила, -сумм орбита. Если ядро находится в состоянии с определенным значением спина и его проекции, то ядро описывается волновой функцией. Спин ядра может быть целым или полуцелым. Спин не превышает 9/2. Спины ядра в основном и возбужденном сост могут быть различными, но всегда целыми или полуцелыми. Спин ядра явл интегралом движения, т.е. сохраняется, но L и S могут не сохран, т.к. ядерн силы – нецентрал. Магнитные моменты: Если есть внешнее эл/магн поле, то поведение ядер обуславливается эл магн моментами. У системы есть и магн момент. У магн момента нет 0-го порядка. Главным считается дипольный магн момент: , где - заряд заряженных частиц. Для нейтронов дипол момент: , при чем м. Магнитный момент ядра складывается из манг моментов протонов и нейронов и орбит момент протонов: ; ; 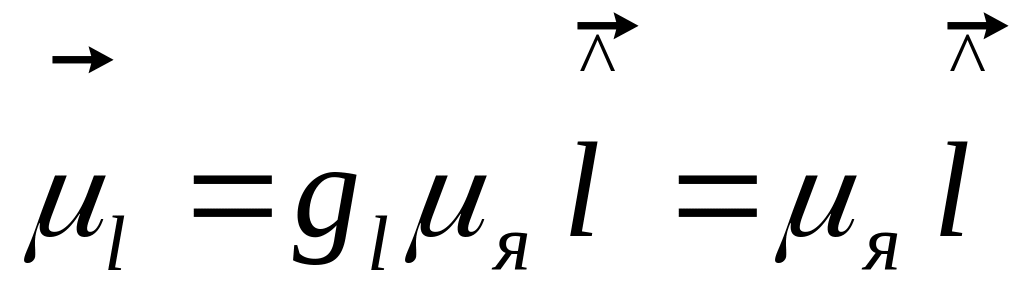=> общ магн момент ядра : У ядра с 0 спином, магн момент =0. Статистика систем: Статистика обусловлена: 1)принципом тождественности одинаковых микрочастиц; 2) вероятностной характеристикой описания состояния квант мех-ки. Любые 2 частицы одного сорта в принципе неотличимы, т.е. состояние системы из двух частиц, ничем не отлич от состояния в котором частицы переставлены местами. Перестановка не приводит сист в новое состояние В квант мех состояния сист опис волн ф-ей: , при перестановке: .Перестановка не приводит сист в новое состояние. Частицам одного сорта свойств-н только один тип перестановочной симметрии. Это св-во частиц по отношению к перестановкам и наз статистикой. Принцип Паули: Для фермионов справедлив принцип запрета Паули: Волн ф-ция системы нуклонов, в принибрежении Эл магн взаимодействием антисимметрична относительно перестановки любой пары. Четность: фундаментальное физ понятие, хар-е св-во любых объектов по отношению к зеркал отражениям. В кв мех четность задает поведение волн ф-ции при пространственной инверсии. В Кл физ говоря, что величина имеет положит четность, если компоненты этой величины не меняются при пространств инверсии и наоборот. Могут быть состояния с положительной, отрицательной и безопределенной четностью. Закон сохранения четности: В сильных и электромагнитных взаимодействиях простран - ственная четность P сохраняется.

49. Трудности теории атомного ядра: 1) Св-ва сил недостаточно изучены и их вид, неизвестен; 2)В ядре, в отличии от атома нет выделенного центра, все нуклоны равноправны; 3)В ядре хотя частиц много, но недостаточно для определения статистическим методом. Классификация ядерных моделей: Универсальной модели, описывающей все св-ва пока нет. Различают: I)Одночастичные модели (учитывает только степени свободы, необходимые для описания отдельного нуклона): а) модель ядерного ферми-газа – простейшая статистическая модель, в которой ядро трактуется как идеальный газ фермионов в ограниченном объеме. При этом поверхностные эффекты не учитываются. Модель позволяет вычислять глубину эффективной потенциальной ямы для нуклонов, позволяет качественно объяснить насыщение ядерных сил, описать испускание частиц ядром, как процесс испарения, и описание распределения нуклонов по импульсам.

б) оболочечные модели – предполагают, что нуклоны двигаются более-менее независимо друг относительно друга в средне-потенциальном поле, создавая движение всех составных эл-ов ядра. Взаимодействие между нуклонами представляется, как воздействие на них самосогласованного поля и некоторого слабого остаточного взаимодействия. Все оболочечные модели различаются методом учета этого остаточного взаимодействия: 1) без остаточ вз-ия (позволяет объяснить знач магн числа, предсказать значение спинов, четностей магн моментов основных сост, дважды магических ядер м ядер отлич от дважды магических); 2) с феноменологическим спариванием (остаточное вз-ие учитывается просто, предполагая, что одинаковые нуклоны объединены в пары с нулевым моментом импульса и с положительной четностью. Модель позволяет объяснить значение спинов и четностей всех чет-чет ядер и почти всех чет-нечет. Позволяет вычислить магн моменты почти всех чет-нечет ядер); 3)Сверхтекучие модели (Обосновывают предположение предыдущей модели на микроскопическом уровне. Идея заимствована из теории сверхпроводящих металлов и сверхтекучести жидкого He. Базируется на предположении о том, что между двумя одинаковыми нуклонами, с равными по модулю и противоположн по направлению моментами или действием специфической силы, объединяя их в пары со спином и четностью 0 ⁺. Для разрыва такой пары требуется энергии ~ (1-2)МэВ. Модель позволяет объяснить значение спинов и четностей основных и многих низших основных состояний, почти всех ядер. Предсказать сверхтекучесть); 4) с остаточным вз-ем (явным образом вводится потенциал остат взаимодействия нуклонов. Модель матем сложная, но позволяет объяснить большое кол-во хар-к ядерных уровней и превращений). II)Коллективные модели (учитывает степени свободы, отвечающие согласованному или коррелированному движению большого числа свобод): а)Модель ядерной материи – изуч св-ва гипотетической, безграничной среды, состоящей из одинак числа протонов и нейтронов. Они взаимод между собой по средствам ядерных сил. Модель позволяет вычислить плотность, удел энергию связи ядерного вещества, позволяет объяснить насыщение ядерных сил, изучает спектры возбуждений и некоторые ядерные реакции; б)Капельная модель – Трактует ядро, как каплю заряженной жидкости, в усложненном варианте, как каплю p-n – жидкости. Степени свободы отвечают небольшим объемом информации и знач поверхностных колебаний. В усложненном варианте, колебание всех протонов относительно нейтронов описывается усредненной зависимостью энергии связи ядра от Z и A, описание поверхностных колебаний сферических ядер и объясняет качественно деление ядер; в)Несферическая модель – Постулирует эллипсоидальную форму некоторых ядер, рассматривает как сгустки вещ-ва, при этом учитываются не только колебательные, но и вращательные степени свободы. В этой модели вещество ядра рассматриваются, как смесь вязкой и сверхтекучей жидкости. Хорошо описывает энерг уровни чет-чет ядер несфер формы. III) Обобщенные модели (учитывают все степени свободы).

Модель ядерных оболочек: В основе модели лежит допущение о самосогласованности поля, т.е. о том, что реальные силы взаимод-ия нуклонов в нулевом приближении можно заменить общим для всех нуклонов силовым центром. Задача сводится к движению одной частицы в поле силового центра. Соответствующий полю потенциал подбирается эмпирически. Решая уравнение Шредингера, для движения нуклона, в самосогласующемся поле, получим некую систему решений. Нуклоны после заполнения энергетических уровней в соответ с принципом Паули. Группа уровней, близких друг к другу по энергии наз оболочкой.

В качестве возмущения возьмем спин-орбит взаимод. Получаем модель, где к сферич потенциалу д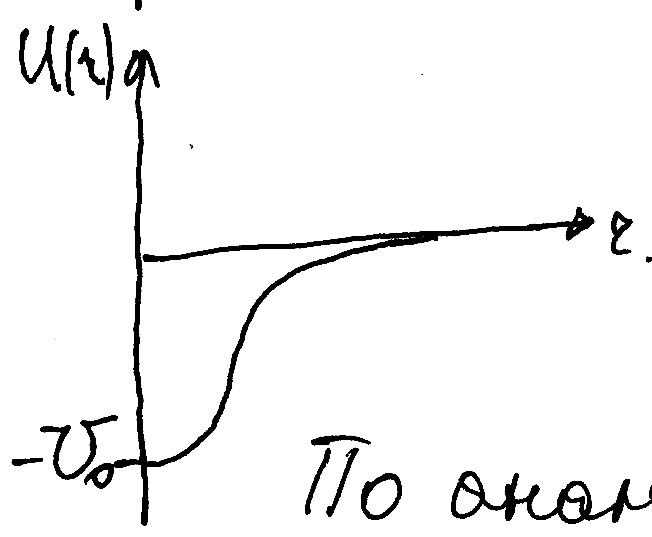 обавляется потенциал спин-орбит взаимод: , где -оператор спина, - оператор орбит. По аналогии с атомом полагают: , где b – const спин-орбит взаимод Потенциал , чаще всего выбирают в виде ямы с пологими краями: . При переходе к другим ядрам, вид потенциала не меняется. Параметры U0, R, b изменяются плавно в зависимости от заряда вещества. Кавнт числа: По аналогии с атомом, используются 4 кв числа: l=0,1,2,.., j(полный момент)=l+1/2, l-1/2, при l=0 => j=1/2; m=-j,..,+j, n- порядок распростран уровней при 49(2)… задан m. При обозначении уровня: n, символизирует орбит моменты, а нижний индекс указывает j: . Порядок и особенности заполнения ядерных оболочек: 1) энергия уровня резче, чем в атоме, растет с ростом n, это связано с тем, что самомогл потенц быстро уменьшается с увеличением расстояния, а среднее расстояние нуклона отцентра ядра увелич с ростом n; 2)энергия уровня уменьшается с ростом l, из-за того, что увеличивается так наз центробежн кинетик энергия , соответствующая орбитальному движению нуклонов; 3)за счет спин-орбит взаимод уровни расчисляются на нижележащие состояния с ( ) и вышележащие с ( ). Возможности применения модели ядерных оболочек: описывает спины, четность, магн момент ядер, в которых один нуклон в сверхзаполн оболочке или одного нуклона не хватае. Для большенства других ядер предсказания этой модели далеко неоднозначно.

50. Группы процессов, в которых прояв ядер силы: Нуклоны в ядре удерживаются ядерными силами, представляющими собой одно из проявлений сильного взаимодействия. Ядерные силы проявляются в трех группах процессов: а) как парное взаимодейст­вие двух свободных нуклонов, приводящее к существованию дейтрона и обусловливаю­щее нуклон-нуклонное рассеяние; б) как взаимодействие свободных нуклонов с ядрами и ядер между собой (наиболее изученное для рассеяния нуклонов на ядрах); в) как взаимо­действие нуклонов внутри ядра, обусловливающее его существование. Основные Основ­ные приближения: 1) двухчастичное приближение - гамильтониан взаи­модействия между А нуклонами определяется суммой гамильтонианов всех парных взаимодействий: 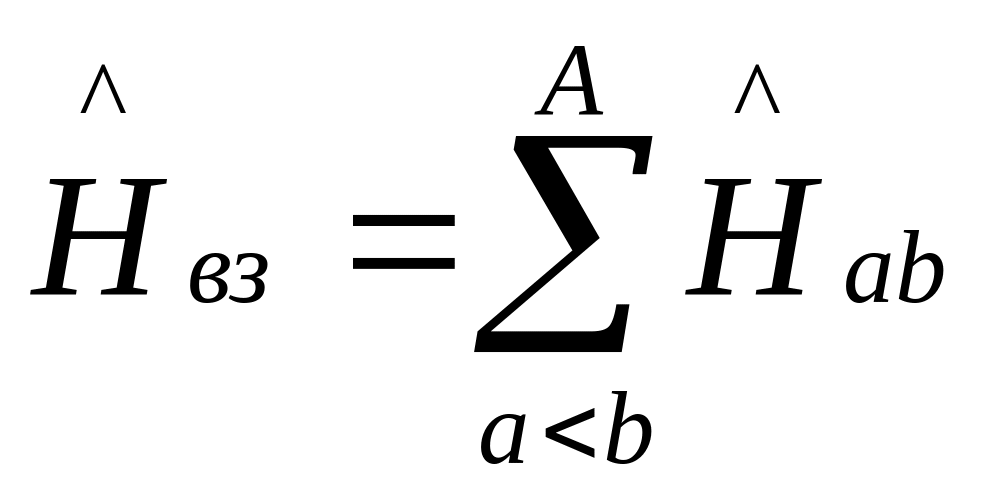. Силы взаимодействия между двумя нуклонами не изменяются из-за присутствия других нуклонов (в соответствии с принципом суперпозиции); 2) ядерные силы можно считать потенциальными (в задачах, связанных с изучением основного и слабовозбужденных сост-ий ядра) - пренебрегаем внутр структурой нуклонов и эффектами запаздывания, т.к. характерные ядерные энергии ~10 МэВ. При этом гамильтониан вз-ия двух нуклонов зависит не только от расстояния между нуклонами, но и от их взаимного расположения, спинов и изоспинов. При этом ядерные силы имеют обменный характер; 3) грубое прибли­жение центрального поля - потенциал ядерного взаимодействия нуклонов зависит лишь от расстояния между ними ( - потенциал Вигнера). Свойства ядерных сил: Ядерные силы интенсивные (на два-три порядка превышают электромагнитные) и имеют конечный радиус действия. На малых (< 0,4 Фм) расстояниях притяжение между нуклонами сменяется отталки­ванием. Это свойство ядерных сил можно описывать, вводя «отталкивательную сердцевину».Ядерные силы зависят от взаимной ориентации спинов взаимодействующих нукло­нов. Ядерные силы нецентральные, т.е. зависят от ориентации спинов относительно пря­мой, проходящей через нуклоны (об этом свидетельствует, например, отличие магнитного момента дейтрона от суммы магнитных моментов протона и нейтрона). Нецентральную часть ядерного взаимодействия называют тензорными силами. Трудности описания ядерного взаимодействия с помощью потенциального подхода: Потенциальный подход к описанию яд-ого вз-ия давал бы хорошие ре­зультаты, если бы у яд-ых сил не было бы других св-в, помимо вышеперечислен­ных. Яд-ые силы обладают также зарядовой независимостью, а также свойством насы­щения (нуклон притягивает небольшое число соседей и отталкивает остальные нуклоны). Обменное взаимодействие, виртуальные частицы: Гейзенберг высказал мысль обменном характере ядерных сил и о суще­ствовании новой частицы, переброс которой обусловливает эти силы. Юкава, зная радиус действия ядерных сил, оценил массу такой частицы. Суть рассуждений сле­дующая. Если состояние квантовой системы существует в течение конечного промежутка времени , то оно не стационарно, и его энергия определена с точностью до . Гипотетическая частица испускается одним нуклоном и быстро поглощается другим, со­стояние всей системы в целом нестационарное. Такие промежуточные реально ненаблю­даемые частицы называют виртуальными; их «существование» не противоречит закону сохранения энергии. ~ тс², где т - масса виртуальной частицы, скорость ее ~ с, тогда , ~ (1-2) Фм - радиус действия ядерных сил. Тогда получаем ~ (200-300)т_е - на два порядка больше массы электрона, но на порядок меньше массы протона. Частицу назвали «мезон». Суть гипотезы Юкавы: ядерное взаимодействие есть результат обмена нуклонов виртуальными мезонами. Суть мезонной теории ядерных сил: Два нуклона, находясь на малом расстоянии друг от друга, обмениваются виртуальными пионами. При этом возможны обмены без изменения

состояния нуклона и с изменением. Отдельный нуклон находится в динамическом равновесии с «облаком» испускаемых и по­глощаемых им виртуальных пионов. Собственно, под нуклоном и следует понимать некий затравочный нуклон с его пионным «облаком». Наличием последнего можно объяснить существование аномальных магнитных моментов нуклонов.Применения и достижения мезонной теории ядерных сил: Объяснила природу ядерных сил и предсказала ряд фундаментальных фактов: существование пионов и их характеристики, большую величи­ну сечения рассеяния пионов на нуклонах, многообразие взаимопревращений частиц с участием пионов. В рамках этой теории впервые была четко сформулирована важнейшая концепция обменного механизма ядерного взаимодействия, перенесенная затем на все фундаментальные взаимодействия. Зарядовая симметрия - равенство ядерных сил в системах (р-р) и (п-п), т.е. между протоном и протоном и между нейтроном и нейтроном. Свидетельства этому: примерное равенство чисел протонов и нейтронов у легких ядер, равенство сечений (р-р)-рассеяния и (п-п)-рассеяния при высоких энергиях, равенство ряда характеристик у зеркальных ядер ( ). Зарядовая независимость - равенство ядерных сил в системах (р-р), (п-п) и (р-п). Она не означает полную тождественность систем (р-р), (п-п) и (р-п) даже в пренебрежении эл магн вз-ием. Всякое состоя­ние системы (р-р) или (п-п) совпадает по своим св-ам с некоторым сост систе­мы (р-п), но обратное утверждение неверно.

50(2) Представления об изоспиновом фор­мализме: Рассмотрим систему двух нуклонов N’ и N’’, операторы изоспина которых и , а оператор полного изоспина . Полный изоспин может принимать значения Т = О (изосинглетное состояние) и Т=1 (изотриплетное состояние). Проекция изоспина протона

Тз = +1/2, нейтрона - Тз = -1/2, поэтому у системы (р-р) Тз = +1, у системы (п-п) Тз = -1, и для обеих систем Т = 1. У системы (р-п) Тз = 0, т.е. возможны состояния с Т = О и Т = 1. Зарядовые волновые функции для системы нуклонов строятся по аналогии с теорией обычного спина. Зарядовая независимость утверждает, что взаимодейст­вия в системах (р-р), (п-п) и (р-п) одинаковы, коль скоро эти системы находятся в одина­ковых пространственно-спиновых состояниях. Это утверждение можно переформулиро­вать: взаимодействия в системах (р-р), (п-п) и (р-п) одинаковы, коль скоро одинаковы изоспины их состояний,т.е. гамильтониан ядерного взаимодействия нуклонов не содержит операторы проекций изоспина. Изоспиновые преобразования: Свойство зарядовой независимости допускает дальнейшую формализацию, если вве­сти в рассмотрение изоспиновые преобразования. При изоспиновых преобразованиях оператор и не меняется (изоскаляр), поэтому свойство зарядовой независимости до­пускает формулировку: ядерное взаимодействие между нуклонами инвариантно относи­тельно изоспиновых преобразований. Зарядовая независимость никак не связана с потен­циальным приближением, т.е. можно говорить не о потенциале, а о гамильтониане ядерного взаимодействия. Математически инвариантность относительно изоспиновых преоб­разований равнозначна коммутативности гамильтониана с их операторами. Тогда еще од­на формулировка зарядовой независимости: в процессах, обусловленных ядерным взаи­модействием, полный изоспин системы нуклонов сохраняется. Нарушение зарядовой независимо­сти электромагнитным взаимодействием: Формально это связано с тем, что полный гамильтониан взаимодей­ствия нуклонов содержит в этом случае оператор заряда, зависящий от проекции изоспина . Гамильтониан коммутирует с , а не с операторами других проекций изоспина, т.е. сохраняется не полный изоспин, а его проекция, что равнозначно сохра­нению электрического заряда. Изоспиновая инвариантность относится к нарушенным симметриям и приводит к приближенному закону сохранения. Обменные силы и их связь с явле­нием насыщения: Для объяснения свойства насыщения ядерных сил были введены обменные силы. Они бывают трех основных типов: 1)силы Майорана (переставляют пространственные коор­динаты нуклонов); 2) силы Бартлетта (меняют местами их спиновые переменные); 3) силы Гей-зенберга (отвечают обмену как пространственных координат, так и спиновых переменных, что равнозначно перестановке изоспиновых переменных нуклонов). При изучении рассеяния бастрых нейтронов на протонах и быстрых протонов на ядерных нейтронах было установлено, что ядерные силы наполови­ну обменные, а наполовину обычные. Силы Бартлетта не годятся для объяснения свойства насыщения; силы Майорана и силы Гейзенберга могут, в принципе приводить к насыщению. Но трудность в том, что ядерные силы не являются чисто обменными. Сейчас считается, что насыщение обу­словлено как обменным характером ядерных сил, так и действием «отталкивательной сердцевины», но проблема объяснения свойства насыщения окончательно не решена.

51. Радиоактивность – любой стабилизированный (занимающий нек промежуток времени) процесс спонтанного распада ядра с превращением его в другоие ядра и ч-цы, т.е , где X-материнское ядро,Y-дочернее ядро, a – ч-цы. Необходимое условие распада: . Энергия распада: . З-н радиоакт-го распада (подчиняется самопроизвол распад): dN= -Ndt – з-н распада в диф.форме, «-»озн, что число ядер с теч вр уменш. dN/N=-dt проинтегр от N до N_o, и от t до 0. ln(N/N_o)= -dt  N=N_o ^{, где} N_o-нач число нераспавш ядер, N – нерасп за вр t. Т.е. число нераспавшихся радиактив ядер убывает со временем экспонициально. Постоянная распада:  - представляет отношение кол-ва атомов, распадающихся за 1с, к числу атомов радиоактивного в-ва, нах внем в данный момент времени или же величина вероятности того, что атом радиоактив в-ва претерпит в течении 1с радиоактив распад. Активность: A=dN/dt – число радиоактив распадов в ед-цу времени, где dN – число распадов за время dt. [A]=1Бк (беккерель) –активность препарата, в котором за 1с происходит 1распад. Период полураспада – время, в течение которого первонач-ое кол-во ядер данного рад/актив в-ва распадается наполовину: T_1/2=ln(2)/=0,693/=0,693τ. Среднее время жизни: τ=1/ - средняя продолжительность жизни всех первонач сущ-ших ядер: . Происхождение ядер: 1)В природе в процессе первичного синьеза хим эл-ов; 2) В природе в процессе первращений, кот претерпевают первичные рад/актив ядра; 3)В природе при действии космических лучей и первичного рад/актив излучения на стабил ядра; 4)В лаборат-х усл-ях при бомбардировке стабил ядер ускоренными ч-ми. Причины стабильности распадов: 1) Гораздо большая стабильность достигается в случае, когда процесс распада энергетически выгодный, но может идти за счет слабого вз-ия; 2)Сущ-т распадные проц-сы с испусканием тяжелых заряж-х ч-ц. Эти проц-сы протекают за счет сильного взаимод-я, но стабильным фактором явл кулонов-й потенц-й барьер. Распад возможен путем тоннельного эффекта. Чем больше m, тем меньше вероятность; 3)Вероятность распада тем меньше, чем меньше энерговыделение,т.е. если вылетающие ч-цы обладают небольшими кинет-ми энерг-ми, то время жизни нестабильного ядра может быть очень большим; 4) При малом энерговыделении вероятность распада сильно зависит от разности спинов материн-го и дочер-го ядр. Чем больше разность, тем меньше вер-ть. 1,2 – опр-т тип рад/актив распада, 3,4 – устанавливают разброс знач-й времен жизни в пределах данного распада. α-распад (характерен для достаточно тяж ядер) – это рад/актив распад, при кот заряд уменш-ся на 2 ед-цы, а массовое число на 4: , где - кинет-я энергия α-ч-ц. Характерной особенностью α-распада явл дискретность энергий α-ч-ц. β-распад – самопроизвольное превращение ядер без изменения их массового числа, с измен-м заряда на 1. Вид β-превращ: 1)с испускание е : ; 2) с испускание протона: ; 3) К-захват (один из протонов возбуж-го ядра способен захватить эл-н из к-оболочки): ; . β-превращ обусловлено превращением самих нуклонов, и связано со слабым взаимод-ем. γ-излучения – рад/актив распад, сопровождающий испусканием γ-фотонов. γ-фотонов поглощается (излучаются) атомами в рез-те перехода их из одного энергетического состояния в другое: , . Спонтанное деление: Способность к протонной рад/активности обладают нейтронодефецитные ядра. Это ядра у кот число нейтронов меньше числа нейтронов у стабильного изотопа этого хим Эл-та. Нейтронодефиц-е ядра получ-т на ускорителях. Н.у и д.у протекания α-распад: α-распад возможен лишь для достаточно тяжелых ядер. В квант-ой мех любой процесс не запрещенный з-ом сохран-ия, протекает с той или иной степенью точности. Поэтому это не только н.у. , но и д.у. распада. Энергия α-ч-ц: 1) Энергия распада α-ч-ц имеет пределы 4-9Мэв для тяжелых ядер и 2-4,5МэВ для редкоземельных (от N=84); 2)У ядер изотопов и на ряду с обычными α-ч-ми вылетают «длиннопробежные» с энергией до 10,5МэВ; 3)Все α-ч-цы из ядер заданного типа имеют примерно одинаковые энергии; 4)Спектр вылетающих ч-ц дискретный; 5) α-ч-цы уносят практически всю энергию, выделяющуюся при α-распаде. Период полураспада: от 3^.10^-7 с до 1,4^.10¹⁷ лет. Полуэмпирический з-н Гейгера-Неттола: T_1/2 очень резко зависит от энергии вылетающих α-ч-ц. Этой зависимости соответствует з-н Гейгера-Неттола: , где С, D – величины, не зависящие от А и слабо зависящие от Z. Особенно хорошо з-н выполн-ся для чет-чет ядер. Основные положения квантовомеханической теории альфа-распада: Считается, что α-ч-ц в ядре уже сформирована. Тогда ее …

51(2)… энергия от центра ядра имеет вид: - энергия отталкивания. В квазистатическом приближении, если ч-ца вылетает в s-состояние, l=0, то U=Uкул, если , то => U=Uкул+Uцб. Т.е. вся кв. мех теория α-распада опис-т все аспекты данного распада. Механизм γ-излучения: Ядро, находясь в возбужд-м состоянии приходит в более низкие энергетические сост не меняя Z и A, но с испускание γ-фотонов. Ядро нах в возбужденном состоянии обычно в результате предшествующих β-распадов. Это происходит каждый раз, когда спины основных состояний материнского и дочернего ядер сильно различаются. Правила отбора: Гамма-кванты, испускаемые ядром при переходе в низшее энергетическое состояние, могут уносить различный момент количества движения L. Излучение, уносящее момент количества движения L = 1, называется дипольным, L = 2 - квадрупольным L = 3 - октупольным и т. д. (излучения с L = 0 не существует из-за поперечности электромагнитных волн). Каждое, из них характеризуется определенным характером углового распределения. γ-кванты различной мультипольности возникают в результате различных «колебаний» ядерной жидкости: электрических (дипольные, квадрупольные и т. д.) и магнитных (дипольные, квадрупольные и т. д.). Процессы первого типа обусловлены перераспределением электрических зарядов в ядре, процессы второго типа - перераспределением спиновых и орбитальных магнитных моментов. Правила отбора при γ-излучении связаны с выполнением законов сохранения момента количества движения и четности. Совместное применение правил отбора по моменту и четности приводит к выводу, что радиационный переход между двумя энергетическими состояниями атомного ядра должен происходить путем испускания двух мультиполей, удовлетворяющих отбору четности: и . Первый из них называют э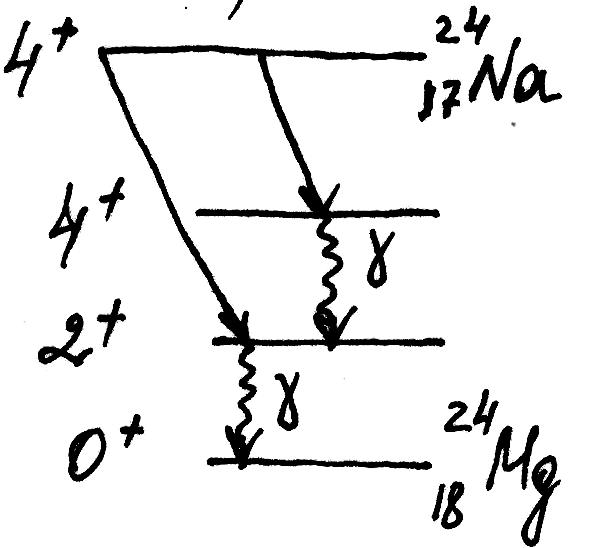 лектрическим (EL), второй — магнитным (ML). Закономерности γ-излучения: Почти во всех из двух переходов, разрешенных правилами отбора, преобладающим является только один - с наименьшим L. Поэтому, изучая γ-излучение экспериментально можно по типу γ-перехода определить четность и изменение спина ядра. Закономерности γ-излучении объясняет сущ-ие изомеров. Изомеры – долгоживущие возбужденные сост ядер. Внутренняя консервация: при ней энергия возбужд-я ядра передается одному из Эл-ов ядерной оболочки за счет обмена виртуальными фотонами, кот могут принадлежать к типу E0 (L=0). Роль ее возрастает с уменьшением энергии перехода. Парная консервация: возможна, если энергия возбужденного перехода превышает 2m_ec², при этом ядро теряет энергию возбуждения за счет испускания виртуального фотона, кот потом превращается в реальную е-р пару. Суть эффекта Мессбауэра: состоит в испускании и поглощении квантов электромагнитной энергии (гамма-квантов) ядрами в твердом теле без потери энергии на отдачу. Дело в том, что атомное ядро, как и атом или ион, может находиться в основном состоянии, то есть состоянии с наименьшей энергией, и в возбужденных состояниях с более высокой энергией. В возбужденном состоянии ядро может оказаться либо в результате поглощения гамма-кванта, энергия которого равна разности энергий между возбужденным и основным состояниями ядра, либо в результате радиоактивного распада. В первом случае происходит поглощение гамма-кванта, во втором – при переходе ядра из возбужденного состояния в основное – происходит его испускание. Если ядра, испускающие или поглощающие гамма-кванты, находятся в состоянии теплового движения (жидкость, газ), то при этом в соответствии с законами сохранения энергии и импульса энергия гамма-квантов будет определяться и состоянием движения ядер. Поскольку скорости движения ядер в газе или жидкости могут быть различными, то и энергии гамма-квантов будут составлять некоторый набор энергий, в результате чего линия поглощения (излучения) окажется широкой. Аналогично при излучении гамма-кванта ядра, сравнительно жестко закрепленные в узлах кристаллической решетки твердого тела, должны испускать (поглощать) кванты практически одной и той же энергии. При этом линия излучения (поглощения) становится очень узкой, ее ширина в отдельных измерениях при низких температурах становится практически равной естественной ширине линии. Именно поэтому эффект Мёссбауэра определяют как поглощение (излучение) гамма-квантов атомными ядрами без потери энергии на отдачу (имеется в виду отдача ядра).

52. Бета-превращения – рад/актив превращения атомных ядер, в кот нейтрон переходит в протон (или наоборот) и участвуют электроны или позитроны, нейтрино или антинейтрино. Ней­трино – частица с нулевой массой покоя, полуцелым спином, она участвует только в слабом взаимодействии и имеет античастицу - антинейтрино. Типы: 1)электронный–распад (образуется электронное антинейтрино): ;2) Позитронный β⁺ : ; 3)К-хахват (электронный захват): ; 4) захват нейтрино и антинейтрино ядрами: , . Энергетический баланс: используем н.у. распада: . Для электронного распада т_х >т_у +т_е. В таблицах даются массы не ядер, а нейтральных атомов: М_у =т_х + Zт_е, М_у = т_у + (Z +1)т_е. Тогда необходимое условие β^- -нестабильности М_х > М_Y. Для β⁺-распада и β^--захвата соответственно получим: М_х >М_У +2т_e, М_х >М_Y; оба процесса превращают протон в нейтрон, но β^- -захват энергетически выгоднее: при М_Y <М_Х <М_Y +2т_е. β^--захват раз­решен, а β⁺-распад запрещен. β-превращ в естественных и искусивенных условиях:

Применим к анализу β -превращений формулу Вайцзеккера. Энергия ядра с нечетным А равна Е = (А-Z)т_пс² + Zт_pс² –с₀А+ с₁А^2/3 +с₂(Z²/A^1/3)+ с₃A{1-(2Z/A³}². Отсюда при заданном А определим Z _β , соответствующее ядру, устойчивому относительно β -превращений:

ф-ла достаточно точно описывает «дорожку β -стабильности» ядер, причем не только четно-нечетных. Тем самым объясняются следующие эмпирические закономерности: 1) при заданных А β -стабильные ядра группируются вокруг равновесных значений с возможным небольшим разбросом в обе стороны за счет индивидуальных свойств ядер; 2) в области Z < ядра нестабильны по отношению к β^--распаду (избыток нейтронов); 3) вобласти Z > ядра нестабильны по отношению к β⁺-распаду и/или β^--захвату (избыток протонов); 4) при малых массовых числах А/2; 5) с ростом массового числа процентное содержание нейтронов в равновесных ядрах растет. Отсюда следует, что при делении тяжелых ядер (в реакторах) образуются β^--нестабильные фрагменты, а при синтезе легких элементов (термоядерные реакции) образу­ются ядра, неустойчивые по отношению к β⁺-распаду и β^--захвату. При этом от ядерного реактора идет поток антинейтрино, а от Солнца - нейтрино. При коллапсе звезд на первом этапе должны протекать реакции β^--захвата с испусканием нейтрино; при этом могут обра­зовываться ядра, аномально богатые нейтронами (отсюда и название «нейтронная звезда»). Особенности β-распада атомного ядра: β^--распад есть переход нуклона из нейтронного состояния в протонное с рождением электрона и антинейтрино; результаты квантовомеханических расчетов в отношении непре­рывного энергетического спектра образующихся электронов хорошо согласуются с опытом. β⁺-распад ядра несколько сложнее, т.к. начальный нейтрон и конечный протон в ядре испытывают воздействие со стороны других нуклонов, на вылетающий электрон дей­ствует сильное электрическое поле ядра, структура ядра при распаде перестраивается. Все это искажает форму β -спектров и затрудняет их теоретическое объяснение. Основные типы нейтрино: 1)электронное; 2)мюонное; 3) таонное. У всех есть античастицы. Основные св-ва нейтрино: После открытия несохранения чет в процессах, обусловленных слабым взаи­модействием, была создана теория двухкомпонентного нейтрино, в которой частицам v и приписывается еще одно квантовое число - спиральность , значениями ко­торого они различаются. λ - удвоенная проекция спина на направление движения, λ= +1 для правовинтового антинейтрино λ = -1 для левовинтового нейтрино. При пространст­венной инверсии v переходит в v и наоборот. Основные типы нейтрино: 1)электронное; 2)мюонное; 3) таонное. У всех есть античастицы. Проблема массы нейтрино: Нет достаточно надежных эксперименталь­ных подтверждений тому, что , но нет и запрета на это. Актуальность проблемы несомненна. Во-первых, знание масс разных сортов нейтрино представляет самостоятельный интерес. Во-вторых, их установление позволит подтвердить или опровергнуть некоторые теоретиче­ские схемы. В третьих, проблема массы нейтрино важна для астрофизики и космологии. Аргумент в пользу ненулевой массы нейтрино - существование «скрытой мас­сы» (возможно, обусловленной нейтрино) во Вселенной в невидимых гало, окружающих галактики и их скопления, которая на порядок больше видимой массы этих объектов. На­личие массы у нейтрино объяснило бы существование «блинов» - сверхскоплений галак­тик. Лептонный заряд: лептонный заряд L (+1 для лепто­нов, -1 для антилептонов и 0 для остальных частиц). Лептонный заряд определяется сум­мой электронного, мюонного и таонного зарядов: L = L_e + L_μ + L_τ. В настоящее время считается, что все эти заряды сохраняются во всех процессах.

52(2) Основные св-ва сл вз-ия: Слабое взаимодействие характеризуется малым радиусом действия, ма­лой интенсивностью, от­носительно большими временами. Непосредственно проявляется лишь в микро­мире. Отличительная особенность слабых процессов - участие в них нейтрино. Слабые процессы служат источниками энергии звезд и влияют на их эволюцию. Слабое взаимо­действие не подчиняется ряду запретов, характерных для сильного и электромагнитного взаимодействий. Проявления сл вз-ия: медленные распады частиц с превращением их в более легкие частицы. Наиболее распространены β -распады (ядер, нейтрона, мюона): . Теория β-распадов Ферми: Согласно этой теории слабое взаи­модействие 4-хфермионное и контактное: непосредственно в нем участвуют 4 фермиона п, р, е^-, , находящиеся в одной пространственно-временной точке. Обозначая полевые операторы рождения и уничтожения символами частиц и вводя нуклонный и электронный «токи» гамильтониан слабого взаимодействия можно записать в упро­щенном виде: . Слабые токи: Ферми считал слабые токи векторными, но в отличие от электромагнитного тока слабые токи заряжен­ные: в вершину соответствующей фейнмановской диаграммы входит нейтральный нейтрон, а выходит заряженный протон. В данной схеме отсутствует аналог фотона, и слабые токи взаи­модействуют непосредственно друг с другом, т.е. взаимодействие контактное. (V-A)-вз-ие: Полный слабый ток строится как сумма отдельных адронных и лептонных токов: j = j_адр + ]_лепт , а гамильтониан слабого взаимодействия имеет вид . Т.о. все токи связаны между собой единым «слабым зарядом» - константой Ферми Gf. Термин (V-A)-взаимодействие означает, что каждый слабый ток представляет собой сумму (или разность) векторного j_v тока и аксиально-векторного тока j_A. Неприменимость методов теории возму: Поскольку теор возмущ не является пе­ренормируемой. Здесь возникает бесконечное число независимых расходящихся диаграмм Фейнмана, для исключения которых требует­ся бесконечный набор эмпирических параметров. Поэтому данный вариант теории слабо­го взаимодействия следует рассматривать лишь как полуфеноменологическую схему, спо­собную приближенно описывать слабые процессы при сравнительно низких энергиях. Обменный механизм сл вз-ия: Посту­лируется существование так называемых промежуточных бозонов, процессы испускания и поглощения которых фермионами (лептонами и кварками) явл элементарными ак­тами слабого взаимодействия. Промежуточные бозоны - векторные частицы со спином J = 1 (пространственная четность им не приписывается, т.к. не сохраняется при их участии в слабом взаимодействии). Испускание и поглощение промежуточных бо­зонов может сопровождаться изменением четности, странности, очарования и т.п. Проме­жуточные бозоны могут участвовать в эл магн и сл взаимодействиях, но не в сильном. Формально промежуточные бозоны - «белые» частицы, т.е. кварк, испус­кающий или поглощающий промежуточный бозон, может изменить аромат, но не цвет. Связь между схемой с промежут базонами и контактной 4-хфермионной схемой: При небольших передаваемых импульсах (т.е. при невысоких энергиях) то обстоя­тельство, что слабое взаимодействие переносится промежуточными бозонами, несущест­венно с практической точки зрения. В этой области энергий те же результаты дает более простая в формальном отношении схема контактного четырехфермионного взаимодейст­вия (поэтому она используется на практике до сих пор). При высоких энергиях необходим учет промежуточных бозонов (но теория все же неперенормируема, поэтому долгое время не получала признания).

53. Ядернаыя реакции – наз превращение атомных ядер, вызванное взаимодействием их друг с другом или с элементарными частицами, это вида: , где a, b – исходная и конечная ч-цы реакции, X,Y – исходное и конечное ядра. Яд-е реакции могут происходить при условии выполнения всех законов сохр-ия: электронного, барионного, всех лептонных зарядов, энергии, импульса, момента импульса. Особенности сечения реакции: С динамической точки зрения яд-е реации хар-ся интегральным сечением и различными дифф сечениями. Эти значения вычисляются на опыте. Каждому выходному каналу реакции выставляется свое выходное сечение : - полное сечение реакции. Сечение реакции для медленных ч-ц могут иметь очень большое значение. Но если ч-ца имеет положительный заряд, то ей необходимо преодолеть кулоновский барьер: . Медленный протон проскачить через такой барьер почти не может. Если а- нейтрон, то кулоновский барьер отсутствует. Они могут реагировать с тяжелыми ядрами, даже будучи очень медленными. Медленные нейтроны имеют большую вероятность осуществления ядер реакции, для них . Классификационные признаки ядерных реакций: 1)По типу налетающих ч-ц; 2)По характеру превращения; 3)По различным ядрам –мишеням (легкие ядра , тяжелые , средние); 4)По энергиям налетающих ч-ц (малые, низкие, средние, большие , высокие, сверхвысокие). Механизм прямых реакций: достаточно энергичная налетающая ч-ца взаимодействует не с ядром в целом, а с каким-то отдельным элементом ядра (нуклоном или группой нуклонов) и передает ему энергию в течении времени 10^-22-10^-21с. Если в прямом проц-се выбивается один нуклон, то яд-е нуклоны считаются не взаимод-ми, но движутся в самосогласованном поле. Если вылетает 2 нуклона, то при описании реакции учт-ся парные корелляции, т.е. взаимодействие между нуклонами также как по оболочечномй модели. Чем больше ч-ц учавствуют в превращении, тем более сложные корелляции приходится учитывать. Механизм составного ядра: протекает не прямо, а в два этапа: , т.е на 1-м этапе ч-ца захват-ся ядром за время равного характерного ядерного времени. В результате образуется составное ядро (компаунд-ядро) в возбужденном состоянии. На втором ядро с* распадается уже за время большее характерного ядерного времени. Это различие связано с тем, что компаунд-ядро не помнит своей предыстории. Спонтанное деление – собственная яд-я реакция. Вынужденное деление – деление ядер в результате ядерной реакции. Под действием нейтронов происходит образование искусственно-радиактивных изотопов, с периодом полураспада > 5000 лет: , последующий распад . Основные условия протекания цепной реакции – реакция, в которой частицы, вызывающие ее (нейтроны), образуются как продукты реакции. Для подержания цепной реакции необходимо, чтобы среднее число вторичных нейтронов не уменьшалось с течением времени. Введем коэффициент размножение k – отношение кол-ва нейтронов в каком-либо «поколении» к числу нейтронов предшествующего «поколения»: . При k>1-развивающаяся цепная реакция; k=1 – самоподдерживающая цепная реакция; k<1 – затухающая реакция. Для стационарного течения цепной реакции нужно осуществить самоподдерживающуюся цепную реакцию. Развивающаяся цепная реакция приводит к ядерному взрыву. Основные типы яд-ых реакторов: 1)гомогенные(делящиеся вещво распр-ся по всему раб-му объему. Этим достигается условие того, что вторичные нейтрино способны захватываться делящимися ядрами более эффективно); 2)гетерогенные (предст-ют из себя отдельные блокиТВЭ {тепло выдел эл-ты} Стальная трубк, покрытая ²³⁸U, по кот течет вода).

К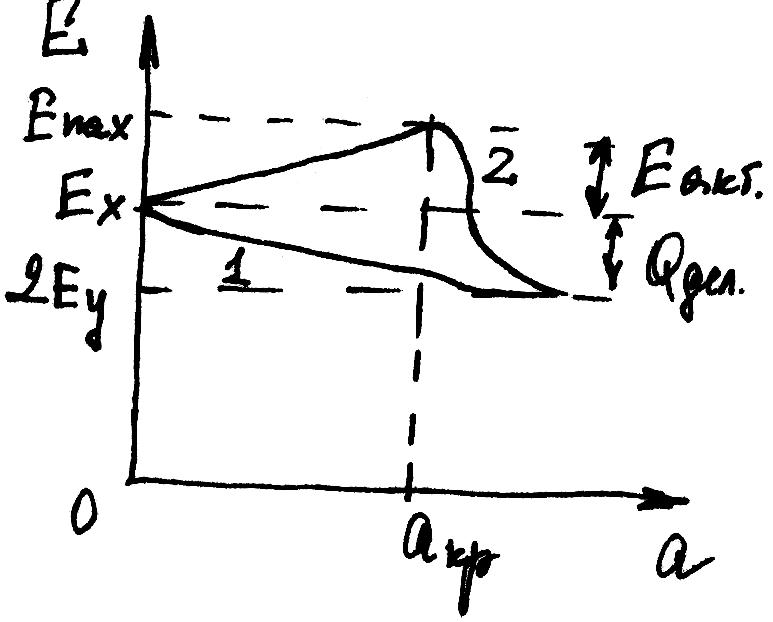 апельная модель ядра: Процесс деления ядра сопровождается глубокой перестановкой ядра и затрагивает все нуклоны, поэтому при ее описании необходимо учитывать многочисленные корелляции, т.е. колич-е степени свободы. В данной модели деление трактуется, как разрыв капли заряженной жидкости. При этом проверхностное натяжение препядствует разрыву жидкости, а кулоновское отталкивание способствует. Если капле сообщ-ся энергия из вне, то возникают поверхностные колебания, кот тоже способствуют разрыву. Энергия активации: 1-мгновенное деление ядра, для кот ; 2- , . При : ; , Разность между и - энергия активации( ).Механизм спонтанного деления: т.е. чтобы ядро развалилось, ему необходимо сообщить из вне энергию возбуждения > . Тогда в проц-се деления выделятся энергия: . С нек вероятностью ядро может разделиться и непосредственно из основного состояния без сообщения энергии из вне. Т.к. массы осколков велики, то вероятность спонтанного деления очень мала. С ростом 53(2) значения энергия активации уменьшается и вероятность спонтанного деления возрастает. Для Крит-го ядра энергия активации обращ в 0 и спонтанное деление происходит мгновенно. При каждом спонтанном делении выделяется значительное кол-во энергии, но источником эти проц-ся служить не могут, т.к. они редкие и неуправляемы. Эффективный порог деления. Особенности реакций под действием нейтронов: Рассмотрим вынужденное деление тяжелых ядер под действием нейтронов. Тепловые нейтроны находятся в термодинамическом равновесии с окруж средой. С помощью захвата до момента деления проходит время. Поэтому образуется , кот делится из возбужденного состояния. Деление происходит, если > . Учитывая: , мы можем получит условие деления ядра: > , где - эффективный порог деления. Начина с А=210, снижается на столько, что деление могут вызвать быстрые нейтроны. Реакция деления ядер теплыми нейтронами энергетически более выгодна. Медленные реакции более надежны, но экономически не выгодны. Все эти процессы мешают делению, но при малых энергиях, неупр рассеяние отсутствует, а вклад остальных проц-в, по сравнению с реакцией распада, очень мала. Запаздывающие нейтроны: спустя 1 мин после реакции с их помощью управл-ся реакция в яд-х реакторах. Устройства в которых осущ-ся управляемая цепная реакция – яд-е реакторы. Необходимо, чтобы коэф-т размножения нейтронов k=1, тогда вторичные нейтрины поддерживают деление ядра. Нейтроны, появляются в рез делении ²³⁵U, обладают энергией 0,7 МэВ. Желательно эту энергию снизить до энергии тепловых нейтронов, т.к. нейтроны с этой энергией эффективно захватываются ²³⁸U и выводятся из цепи деления. В качестве замедлителей применяют легкие ядра, напр водорода, но у него высокое эффектив сечение захвата нейтронов. Поэтому водород не желательно применять. В основном применяют графит.

54. Термоядерная реакция синтеза: Реакция синтеза – процесс слияния ядер с образованием более тяж ядер. Основное препядствие к протеканию такой реакции – кулоновский барьер. Участвовать в реакциисинтеза могут ядра с достаточно большими кинет энергиями. Получить эти энергии можно двумя способами: 1)разогреть реагенты до высокой температуры; 2)большая плотность. В 1-ом случае реакции наз термоядерными, во 2-ом – пиктоядерными. Особенности: Для термояд реакций может оказаться так, что реакция будет самоподдерж, т.е. необходимая температура получится в ходе реакции. Термояд реакции возможны при температуре Т<10⁹К, часть ядер имеет энергию выше средней, работает туннельный эффект. Обычно такие реакции протекают в природе. Пример: водородная бомба, процессы на солнце. Условия, необходимые для протекания: Наиболее эффективна следующая реакция: МэВ (*), для этой реакции характерен сравнительно низкий кулон барьер и сравнительно большое сечение реакции при относительно невысоких энергиях. Энергия, выделившаяся на 1 нуклон, составляет q=3,5 МэВ. Так же возможны следующие реакции: МэВ и МэВ. Для того, чтобы реакция (*) произошла, необходима температура ~ 10⁸К. Эта проблема в принципе решена, возможно получить температуру ~ 10⁷К, при помощи плазмы. Сквозь плазму пропускают элект ток и она нагревается (омический метод), но при высоких температурах возникает пинч-эффект (разрыв нити плазмы). Но и эта проблема решена, в место образующегося разрыва впрыскивают высокоэнергетич ч-цы. На данный момент не решена проблема удержания плазмы. Оценим параметры плазмы, в котор возможна стационар термояд реакция. Число актов синтеза в объеме определяется так: , где -концентрация дейтрона, -концентрация трития, -время удержания плазмы, -энергетическая зависимость сечения реакции. В одном акте выделяется энергия Q: - энергия единичного объема. . С другой стороны, на разогрев плазмы также нужно затратить энергию: => должно быть > => . Если исследовать ф-лу на экстремум, правая часть будет min, если => . С увеличением Т, ф-ция в области низких температур убывает из-за возрастания сечения реакции, а в области высоких температур возрастает из-за множителя Т, т.е. при Т=Т₀ => f=f_min , т.е. температура Т₀ - - наиболее благоприятная для управляемого термояд синтеза. Критерий Лоусона: Произведение концентрации реагирующих ядер на время удержания, в течение которого они сохраняют указанную энергию, должно быть не менее 10¹⁴ с.см^-3. Это условие - определяет предел энергетической выгодности реакции. , где n – концентрация частиц, - время удержания. Пути осуществления УТС: 1)Наличие сверхвысокой температуры; 2)Длительное (более 1с) удержание плазмы в ограниченном объеме; 3)Термоизоляция от окруж среды. Суть принципа токамака (ТОроидальная КАмера с МАгнитными Катушками) - тороидальная установка для магнитного удержания плазмы. Плазма удерживается не стенками камеры, которые не способны выдержать её температуру, а специально создаваемым магнитным полем. Особенностью токамака является использование электрического тока, протекающего через плазму для создания поля, необходимого для равновесия плазмы. Другие пути осущ термояд синтеза: Главный итог термояд синтеза – превращение 4 p в ₂He⁴ c испусканием 2e⁺, 3g, u_e .Это можно осуществить 2-мя способами: 1) Углеродно-азотный цикл: ₆C¹² +₁H¹®₇N¹³+g; ₇N¹³®₆C¹³+e⁺+_e; ₆C¹³+₁H¹®₇N¹⁴+g; ₇N¹⁴+₁H¹®₈O¹⁵+g; ₈O¹⁵®₇N¹⁵+e⁺+u_e; ₇N¹⁵+₁H¹®₆C¹²+₂He⁴. 2) Водородный цикл: ₁H¹+₁H¹®₁H²+e⁺+_e; ₁H²+₁H¹®₂He³+g; ₂He³+₁H¹®₂He⁴+ ₁H¹+₁H¹ . Зависимость: Интенсивность этих реакций, тесно зависит от температуры. q – удел энерг выделения в 1 времени Для ☺ q = 10^-4Дж/(кг^.с).

55. Классиф.признаки микроч-ич: По отношению к сильному в/д: адроны и лептоны. По времени жизни: стабильные (τ>>10^-23c), резонансы (τ~10^-23c). Стаб-ые ч-цы распадаются за счёт слабого и эл/м в/д. Все резонансы (адроны) расп-ся за счёт сильного в/д. По типу стат-ки: фермионы и бозоны. По хар-ру поведения в процессах, обусловл. только сильным в/д, изомультиплетные (семейства, члены которых тождественны по отношению к сильн.в/д-ию, а различия – за счёт эл/м в/д-ия).

Отдельные ч-цы различают по массе, соотв-им квант. числам, зарядам. Каждой ч-це сопоставляется своя антич-ца, иногда с ней совпад-ая.

Х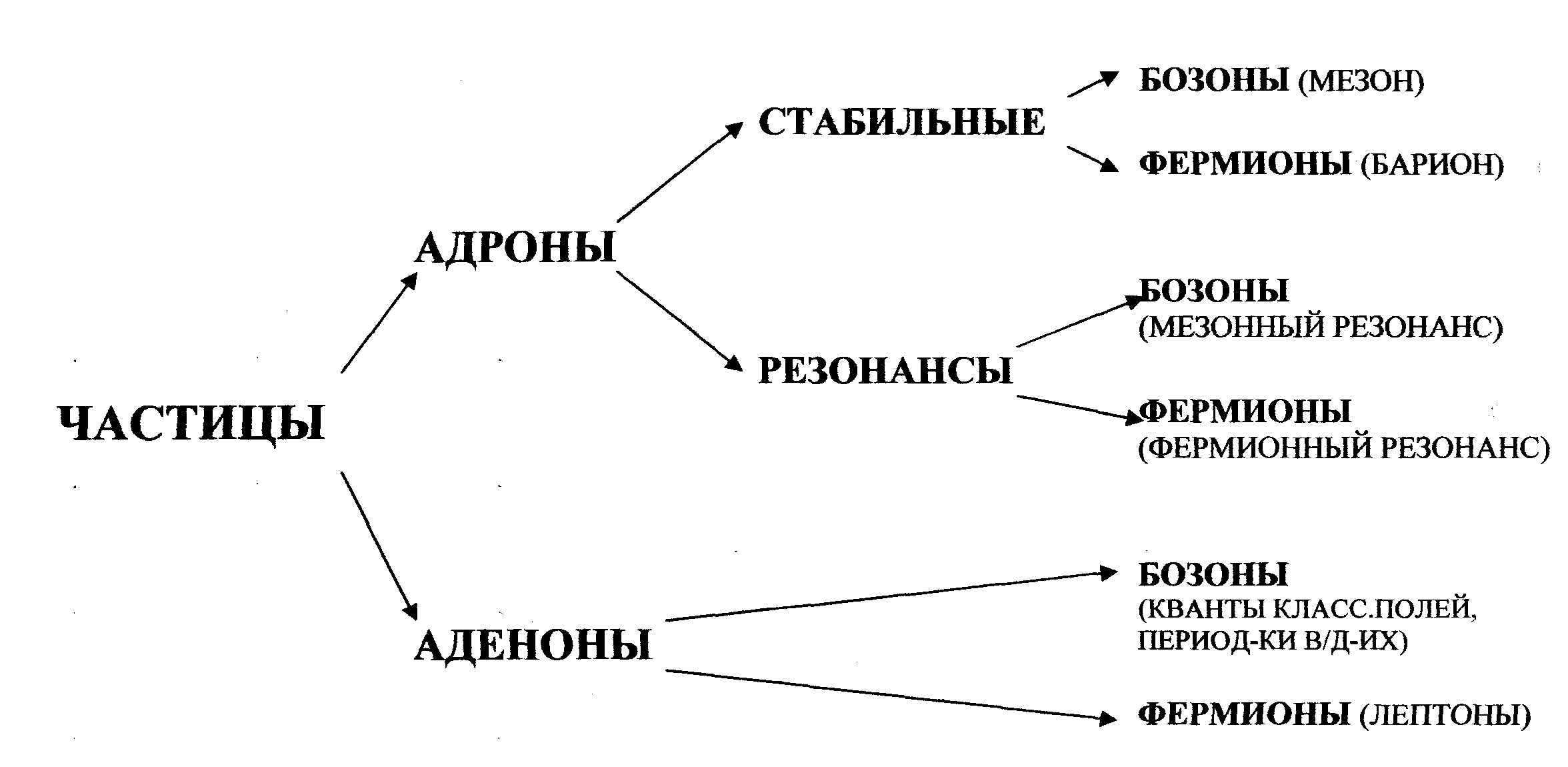 ар-ки частиц: А) геометр-ие – связ. с симметрией простр-ва и времени.

Б) внутренние (масcа М, простр. чётн-ть η,спин I)

Остальные хар-ки (кроме эл/м мом-ов) отн-ся к др. группам.

1) Масса (М): ни какой видимой закономерности в спектре масс нет. Она имеет динамич. происх-ие и должна выч-ся теор-ки. Поэтому не может служить осн-ым классификац-ым признаком.

2) Спин(I): Измеряется в единицах ћ, может принимать целое и полуцелое знач. Ч-цы с I=0 опис-ся скалярными волновыми фун-ми; с I=1 – векторными; с I=1/2 – спинорными. Для покоящейся ч-цы только в-ор спина задаёт выделенное направление.

3) простр. чётность (η_p). Определяет поведение волн-ой ф-ции ч-цы относительно простр-ой инверсии. Если ф-ция не меняется, то η_p=+1, иначе η_p=1. Собственно ч-цу, а не её состояние хар-ет внутренняя простр. ч-ть, У всех стаб. барионов чётн-ть положит-ая, для лептонов ч-ть не вводится.

4) эл. заряд: (q) – измеряется в единицах элем-го заряда е.

5) магнитн. момент (μ): хар-ет в/д покоящ-ся ч-цы с внешним магн. полем. Измер-ся в ед-цах соотв-го магнетона μ₀=eћ/2m.

6) лептонный заряд (L): L=+1 (лептоны), L=-1 (антилептоны), L=0 (остальн.ч-цы). L=L_e+ L_μ+ L_τ.

7) барионный заряд (B): B=+1 (барионы), B=-1 (антибарионы), B=0 (остальные). Явл-ся аддитивн. числом

8) изоспин (T): припис-ся изомультиплету и опред. число членов в ф-ле N=2T+1; T[0;3/2], т-ко барионы.

9) проекция изоспина (T₃): различает отдельные члены изомульт-та; T₃[-T;T].

10) странность (S): вводится так, чтобы эл. заряды удовлетв. соотнош-ию Гелл-Манна-Ниш.: q= T₃+(B+S)/2

11) гиперзаряд (Y): Y=B+S; q= T₃+Y/2

12) очарование (шарм)(С): вводится аналогично странности q= T₃+(B+S+С)/2.

13) зарядовая чётность (η_с).формально сходна с пространственной.

14) среднее время жизни (τ): для стабильных ч-иц ещё указ-ются каналы распадов и вероятности распадов.

Законы сохр-ия: А) В класс. физике законвы сохр-ия вытекают из известных динам-их уранений и играют подчиненную роль. Они выступают в кач. «з-ов дозволения», т.е определяют, что может происходить с системой, но не обязат. происходит. Число з-ов строго ограничено, они связаны, в осн, со cв-вом симметрии простр-ва и времени. З-ны сохранения строгие.

Б) В квантовой физике з-ны сохр-ия – единств-ый источник инф-ции о св-вах и поведении ч-иц. Они имеют хар-ер запрета, т.е опред-ют, чего не может происходить с системой. Число з-ов оч. велико. приближен. з-ны сохр.. Нек-ые величины сохр-ся не во всех в/д-ях. Чем интенсивнее вз-ие, тем больше для него з-ов сохр.

В) Универсальные з-ны сохранения (справ. для всех типов вз-ий):

1. З-н сохр-ия 4ёх импульса Р

2. З-н сохр-ия мом-та имп-ся I

связан со cв-ом изотр-ти простр-ва (равноправие всех напр-ий). Характеристикой ч-иц, а не их сост-ий служит один из компонентов мом-та имп-са.

3. З-н сохр-ия электр. з-да q

 это следствие калибровочной инвариантн-ти, т.е ковариантность эл/дин-их у-ий отн-но калибровочных преобразований, кот-ые затрагивают не координаты, а волновые ф-ции. З-н сохр-ия заряда обеспечивает стабильность заряда эл-на.

4. З-н сохр-ия лептонного заряда (L(L_e, L_μ, L_τ))

 родственен с №3, возм. выполн-ся приближённо (если m_0, приближённость з-на может привести к нейтринным осцилл-ям)

5. З-н сохр-ия барионного заряда (B)

 связан с калибровочной инвариант.. Его следствие – абс. стабильность протона…

55(2) Сильное в/д – наиболее симметрично (в нём сохр-ся все 5 законов),

Эл/м в/д – менее симм-но (в проц-ах не сохр-ся изоспин, а T₃ сохр-ся.

Слабое в/д – наименее симм-но (в проц-ах выполн-ся т-ко универсальные з-ны сохр.)

Пространственная ч-ть η_p связана с преобразованием простр-ной инверсии, а её сохр-ие с зеркальной симм-ей простр-ва. Сохр-ие η_p , означает, что процессы в реальном мире и в мире, получ-ом при зерк. отражении, протекают одинаково. Несохр-ие чёт-ти имеет универс. хар-ер и проявл-ся во всех проц-ах, обусл-ых слабым в/д, т.е имеет место зеркальная ассиметрия.

Сильное и эл/м в/д-ия инвариантны отн-но преобразований P^ и C^ по отдельности. Слабое в/д не инвариантно отн-но P^- преобр-ия.

Комбинированная чётность. Истинно нейтральные ч-цы обладают определёнными значениями зарядовой чётности η_с. Тогда им можно приписать комбинированную чётность η_pc=η_p η_c. Это число является собственным значением оператора C^P^.

Обращение времени. Считается, что все процессы в микромире обратимы во времени (за редк. исключ). Но в макромире имеется очевидная направл-ть течения вр-ни в проц-ах. Её связ-ют со 2 нач. термодин-ки.

С^P^T^ - преобразование: Нач. и конечн. состояния поменяются местами (P^), част-цы заменятся антич-ми (C^), импульсы останутся неизменными, проекции спинов изменят знак. (T^- преобр), n/t новый проц. отлич-ся от старого, но тоже может протекать с той же вероятностью. CPT- преобр-ие есть преобразование инвариантности.

Результат приводит к : 1) массы и времена ч-ц и антич-ц строго равны;

2) эл/м моменты отлич-ся т-ко знаком

3) в/д ч-иц и антич-иц с гравитац-ым полем одинаковы, т.е антигравит-ции нет.

Сохранение комбинированной ч-ти равнозначно обратимости микропроц-ов во времени.

В следств. нарушения C^P^ - инвар-ти имеется абсолютное различие между ч-ми и антич-ми, а т.ж. между правым и левым. Значити T^ - инв-ть нарушается. в микромире возм. направл-ть времени.

56. Сильное в/д: присуще т-ко адронам. Оно самое инт-ое. Рад. действ R~10^-15м,

Характерные времена τ ~(10^-24-10^-23 )c. Наиб. известн. проявление – ядерные силы. Сильн. вз. обуславливает процесс рассеяния адронов, рождения адр, распада резонансов, процессы множ-го рожд=ия адр-ов. Оказ-ет косвенное влияние на проц-сы, обусл-ые эл/м и слаб вз-ми (в частн. β-расп. нейтронов).

Адроны нельзя разбить на сост. части, но они имеют внутр. стр-ру. Они состоят из кварков. Кв-ки нах-ся в пожизненном заключении в адронах – конфайнмент кварков. Протоны и нейтроны сост. из лёгких кварков u и d, у них спин ½. p=UUd, n=UUd. Из тех же 2ух кварков может быть построено множ-во ч-иц: Δ⁺⁺=UUU, Δ⁺=UUd, Δ⁰=Udd, Δ^-=ddd. Принцип Паули не наруш-ся, т.к.ч-цы отлич-ся цветом кв-ков.

Мезоны сост. из кварка и антикв-ка, а барионы из 3ёх кв-ков. Кварки отлич-ся цветом (R,G,B). Известно 6 кварков: очарованный (С), странный (S), верхний (U), нижний (d), красивый (b), истинный (t) – ароматы кварков. Конфайнмент означает, что в адронах кварки заключены. В кажд. адроне 3 кварка разных цветов – получ-ся белая ч-ца.

Глюоны – переносчики сильного в/д. Их 8 видов, они безмассовы и в/д между собой. им прсущ конфайнмент.

В модели струн считается, что глюонное поле между кварками, разнесёнными на достат-но большое расстояние, в рез-те сжимается в тонкую трубку (струну). Если их разнести на большое расстояние, то энергия глюонного поля, накапливаемая в струне, становится достаточной, для рождения кварк-антикварковой пары. Глюонное поле при значительном разнесении становится плоским. Энергия 2ух достат-но тяжёлых кварков U=-q/r + br

Партоны: В рез-те опытов рассеяния на протонах, у последних была обнаружена внутренняя структура: e^+p→ e^+адроны. Получалось, что протоны состоят из 3ёх частиц (партонов). Впоследствии выяснилось, что это кварки.

Современная систематика фундаментальных частиц:

Кварки: (адроны)	U	c	t
	d	S	b

Лептоны:	e	μ	τ
	e	μ	τ

и соответствующие им античастицы.

Переносчики взаимодействий: 1)эл/магн: γ-квант, 2)слабого: W⁺, W^, Z⁰- бозоны 3)сильного: 8 глюонов (g)

Изомультиплеты – неболшие семейства, члены которых тождественны по отношению к сильному в/д, а различие засчёт эл/магн. взаимодействия (Пример: нуклон – изодублет n и p)

В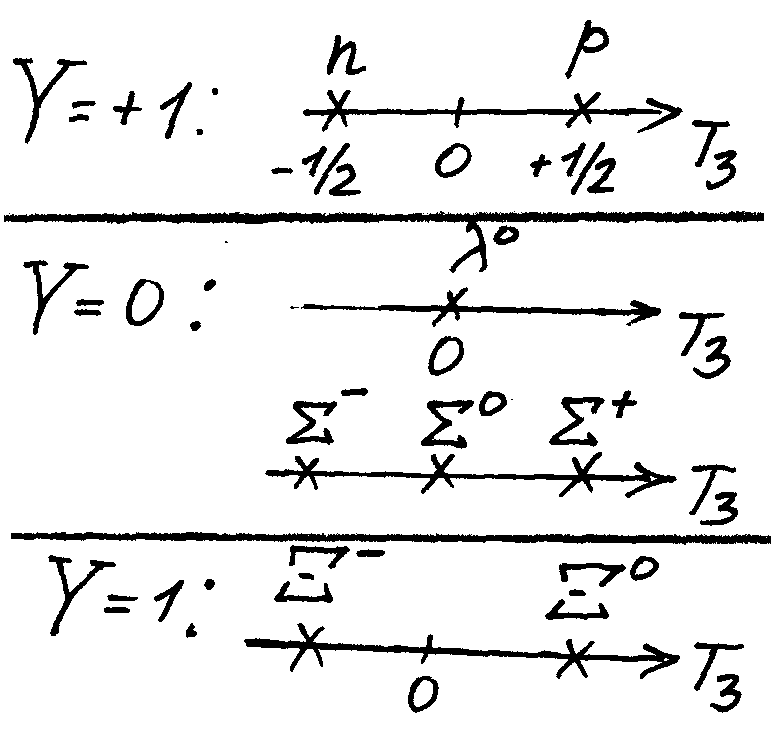 озникал вопрос о классиф-ции адронов: Гелл-Манн&Нишидж. предложили схему класс-ции адронов по изомультиплетам: Каждому изом-ту приписали изоспин и гиперзаряд (T и Y ). Каждый из изомульт-ов обладает эл. спином I, чётностью η_p, барионным зарядом B и почти одинак. массой M, но разными проекциями изоспина T₃ и разным зарядом q. Число членов изомульт-та: N=2T+1, заряд q= T₃+Y/2, Y=B+S

Теоретич-ая основа этой схемы – инвариантность сильного в/д отности-но изоспиновых и калибровочных преобразований с заменой эл. заряда на гиперзаряд. Для всех частиц B=0, I^η =1/2 ⁺ .Математически, изоспиновые преобразования трактуются как вращение в 2 мерном комплексном простр-ве. Такие преобразования составляют группу SU(2).

П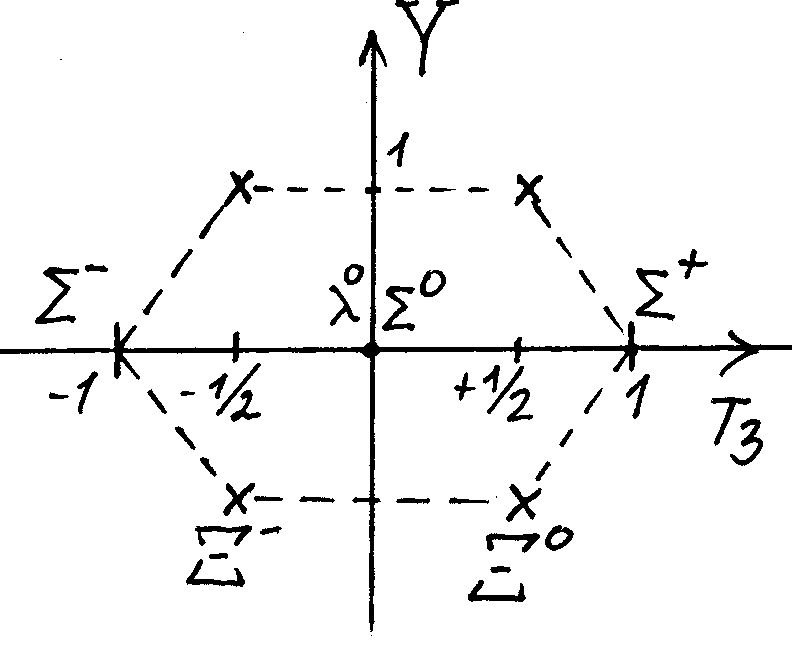 осле открытия резонансов схема стала очень узкой. Новая схема (Гелл-Манн-Нееманн). Получили совокупность 8 частиц. Для всех частиц B=+1, I^η =1/2 ⁺ .Полученные картинки отвечают симметрии, вращение в 3-мерн. комплексн. простр-ве. Эта симметрия наз. унитарная симметрия. Порождаемая этой схемой классификация адронов – 8-ный формализм.