Распределение энергии, ф-лы Рэлея-Джинса и Вина:

Вин, воспользовавшись Эл/м теорией, показал, что функция спектрального распределения должна иметь вид: f(,T)= ³F(/T)-формула Вина, где F – некоторая ф-ция отношения частоты к темп-ре.

Рэлей и Джинс, исходя из закона равнораспределения энергии по степеням свободы, приписали каждому колебанию энергию <ε>, равную kT и получили выражение для испускательной способности АЧ тела:

 формула Рэлея-Джинса.

Интегрируя выражение для плотности энергии по  в пределах от 0 до  даёт для равновесной плот-ности энергии u(T) даёт большое значение - т.н. УФ-катастрофа. Равновесие между излучением и излучающим телом устанавл-ся при конечных значениях u(T)

Гипотеза Планка:

Ф-ла Р-Дж расходится с экспер. для малых λ. Чтобы получить теор. зав-ть совпадающую с опытом, Планк. предположил процесс излучения, осущ-ся отдельными порциями Е_кв=ђω:

Ф ормула П переходит в формулу Р-Д при: (ђω/кТ)<<1, в формулу Вина при: (ђω/кТ)>>1.

Планк считал, что это рабочая гипотеза, к-я позволила получить соотв-ую кривую распределения в спектре излучения абс. черного тела. Но эта гипотеза не вкладывалась в рамки классич. физики.

Фотоэффект  это явление выбивания светом электронов с поверхности металлов. Эксперим-но его открыл Герц в 1887г. Основные закономерности:

1) i_нас~Ф (Ф₂>Ф₁). Ток насыщения ~ падающему световому потоку

2)Если u=0, то i_ф≠0 - выбитые электроны обладают запасом Е_к, засчёт которой долетают до анода.

Опыт показывает, что Е_к не зависит от интенс-ти светового потока Ф, т.е. mv²/2=eu_зап=E_к, E_к~ν.

3) красная граница фотоэф. Если _кр, то i_ф≠0 (фототок есть). Если _кр, то i_ф=0. _кр- зав.от рода мет.

Фототок появляется мгновенно при включении света при  интенсивностях света.

Но согласно волн. теории E_к~Ф(свет. поток), а не .

Гипотеза Эйншт: Свет рождается в виде квантов и  в их виде до поглощения. Квант света в/д с 1эл-ом. Поглощаясь эл-ом, он передаёт импульс и эн-гию, а сам исчезает.

Свет – поток фотонов (квантов). Интенс-ть света – энергия 1кванта, умнож-ая на их количество: E=ђ

38(2) Ур Эйншт: Свет погл-ся такими же порциями, какими исп-ся ђ=А_вых+mυ²/2 – з.сохр.эн-гии, P_Ф= ђ/с

Эфф.Комптона: Рассеяние рентгеновских лучей на опыте расходилось с класс. теорией рассеяния.

Комптон установил, что в рассеянных лучах, наряду с излучением первоначальной длины волны  содержатся также лучи большей длины волны ’>.

Объяснение: Рассеяние – процесс упругого столкновения рентгеновских фотонов с практически свободными электронами (наименее связ-ми) _Комп.=2πђ/mc – комптоновская длина волны.

В состоянии равновесия распределение колебаний по значениям энергии должно подчиняться закону Больцмана. Вероятность P_n того, что энергия колебания частоты ω имеет значение ε_n определяется выражением

можно найти среднее значение этой энергии

тогда . Обозначим и допустим, что x может изменяться, принимая непрерывный ряд значений. Тогда (1)

Подставив в (1) и выполнив дифференцирование получим: . Заменим и получим среднюю энергию излучения частоты ω (2). При ф. (2) переходит в классич. .

Получим плотность энергии, приходячуюся на интервал частот :

(3)

(4)

Выражражения (3) и (4) носят название формулы Планка.

39.В 1911 Резерфорд со своими учениками проводил опыты по рассеянию α-частиц(2х-кратно ионизир. атом He) на золотой фольге. Одна из 1000000 частиц обнаруж. под углом, близким 180. Почему положительно заряженная частица изменяла направление на противоположное. Вспомним закон Кулона. Такое отражение возможно от тоже положительной и более массивной частицы. На основе этого Резерфорд оценил размеры этого препятствия:~10^-15м. На основе этого он предложил ядерную модель атомов. По Резерфорду: атом состоит из положительно заряженного ядра, размерами~10^-15м, вся масса атома практически сосредоточена в ядре, а вокруг ядра в объуме~10^-10м сосредоточены электроны. Вцелом атом нейтрален. В последствии Резерфорд пришел к планетарной модели атома, электроны в атому вращаются подобно планетам, вокруг Солнца-ядра по своим орбитам. Эта модель имела существенный недостаток: согласно классической электродинамике заряженная частица(электрон), движущаяся ускоренно должна излучать энергию в виде электромагнитного поля→орбита такого электрона должна представлять спираль, в итоге электрон должен свалится на ядро. а атом прекратить свое существование. Не сложный расчет показывает. что это должно произойти через 10^-8 -10^-12с.

Постулаты Бора:1). Атом может находится в строго определенных состояниях, характеризуемых значениями энергии: E₁, E₂, E₃…… Находясь в этих стационарных состояниях, атом не излучает и не поглощает (стационарные или квантовые состояния). 2). При переходе атома из стационарного состояния с энергией E_м в стационарное состояние с меньшей энергией E_n , происходит излучении энергии, величиной .

Т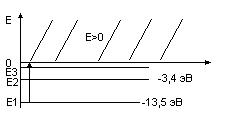 еория Бора: Найденные дискретные значения энергии E₁, E₂, E₃…… E_n –называются квантовыми энергиями. Для большинства хим. элементов их значения находятся с помощью квантовой механики. Бором была предложена теория, позволяющая найти эти значения для водородоподобного атома-атом с ядром, вокруг которого вращается один электрон. Примером такого атома является атом водорода, однократноионизированный атом He. В своей теории Бор предполагал, что электрон вращается по круговой орбите. В этом случае кулоновская сила между электроном и ядром-центростремительная. Используя систему найдем радиусы орбит, скорость электрона при его нахождении на разных орбитах: Радиус зависит от главного квантового числа n.→ . Полная энергия атома слагается из Т=Е_к электрона и Е_n-взаимодействия электрона с ядром. -дискретная величина. Исходя из схемы распределения энергетических уровней, при n→∞, законы квантовой физики переходят в законы классической физики. когда система может обладать любым значением энергии-пинцип соответствия Бора.

При n → ∞, En → 0 и дискретн. Спектр перех. В непрерывн. Е ионизации = Есв = |E1|.

При переходе электрона с m-ого эн. уровня на n-ый происходит излучении энергии величиной: -спектроскопическое волновое число. → , приz=1.К-постоянная Ридберга. Эта теория блестяще описывает поведение водородоподобного атома и атома водородаюТеория эта не до конца классическая и не квантовая, и не применима для др. атомов.

Спектральные серии атома водорода. Исторически принято характеризовать положение спектральных линий спектроскопическим волновым числом: . Спектры бывают: линейчатые(атомарные), полосатые(молекулярные). Как правило, спектр химического элемента состоит из отдельных серий. Различают след. спектральные серии атома водорода:

1). Серия Лаймана(1916): -ультрафиолет.

2). Серия Бальмера(1908): -видимый диапозон(син-красн).

3). Серия Пашена(1922): -ближняя ИК область.

4). Серия Бреккета: -дальняя ИК область.

5). Серия Пфунда: - дальняя ИК область.

-=1.097*10⁷ м^-1 – постоянная Ридберга для водорода.

Опыты Франка-Герца: 1914 они явились экспериментальным подтверждением постулатов Бора. Франк и Герц поставили эксперимент, который подтвердил дискретность энергетических уровней. Опыты показали, что энергия поглощается строго определенными порциями (рис).

З адача о движении микрочастицы в центрально-симметричном поле сводится к совместному решению системы 3х уравнений: . Решение данной системы сводится к решению радиального уравнения Шредингера: . Возьмем конкретное выражении для потенциальной энергии: -кулоновское поле. Оно реализуется в водородоподобных атомах(ионах) с одним электроном в оболочке. Т.о. рассматриваем задачу о водородоподобном атоме.

При решении данного уравнения с такой потенциальной энергией, можно получить следующие выражения для допустимых значений энергии, абсолютной величины момента и его проекции на заданное направление: (*) , где n=1,2,3,….-главное квантовое число. Получили формулу для энергетических уровней водородоподобного атома. , где l=0,1,2,…,n-1-орбитальное квантовое число. , где m=0,±1, ±2,…., ±l-магнитное квантовое число.

Волновая функция ,которая является решением системы, зависит сразу от 3х квантовых чисел: . Каждая такая ф-я является собственной ф-ей 3х операторов, значит каждая такая функция описывает состояния водородоподобного атома с определенным значением энергии, абсолютной величины момента импульса, проекции момента импульса, зад. соот. формулами. Волновые функции описывают квантовые состояния водородоподобного атома. Квантовым состоянием системы называется состояние, в котором все величины полного набора имеют определенные значения(не путать квант. сост. с энерг. сост. В энерг. сост. определенное значение имеет только энергия, в квант. сост. все 3 величины явл. энергетическими).Одному эн. сост. может соот. несколько квант. сост. Для водородоподобного атома одному энергетическому состоянию будет соответствовать квантовых состояний(кратность вырождения).

Совпадение: формула (*) для зн. совпадает с ф-лой, полученной в рамках теории Бора. Отсюда формулы для частот совпадают. Спектры излучения и поглощения совпадают. И совпадают с экспериментом.

Различия: 1) согласно теории Бора в низшем энергетическом состоянии атома момент импульса отличен от нуля m₀vr = mћ, m соответствует м в кв. механике, где м=1,2,3 – номер орбиты. Согласно кв. мех. при l=0 => L=0 и Lz =0. Низшее энергетич состояние: в т. Бора n=1, m=1 (отличен от 0) В кв.мех. n=1, l=0 => m=0.

2) В т.Бора сохраняется понятие траектории (орбиты). Эл-н можно обнаруж. только на строго определ. расстоян. от ядра. В кв. мех. вероятн. обнаруж. эл-на на том или ином расст. от ядра определ. квадратом м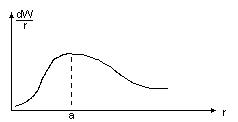 одуля радиал. волн. функ. . зависимость пл-сти вероятности обнаруж. В радиальном направлении. Плотность вероятности определ-сти (рис)

а – радиус первой боровской орбиты. Согласно кв. мех. эл-н можно найти на любом расстоянии от ядра. Кв. мех. уточняет т. Бора.

40. Гипотеза де-Бройля В нач 20 в. Сложилось представл о корп-волн дуализме света. В 1923 ДеБройль выдвинул гипотезу универсального корпускулярного волн. дуализма. Согласно ему с каждым микрообъектом связаны корпускулярные хар-ки (E и p), а с друг.стороны – волновые ( и λ). E=h, p= h /c= h /λ

Гипотеза ДеБ постулировала эти ф-лы даже для частиц имеющих массу : . Каждой ч-це ДеБ сопоставил каждой частице плоскую монохромат.волну ψ(r¯,t)= ψ₀ exp i(k¯r¯- t)

Правильность гипотезы де-Бройля была подт-на в опытах Тартаковского и Томсона и Дэвиссона-Джермера. Идея опытов состояла в том, чтобы получить явл-ие дифракции с помощью микроч-ц.:

пучок эл-нов направл-ся на дифр решётку. Что взять в кач-ве решётки? p=2πћ/λ_∂, (корень 2mE_k)=2πћ/λ_∂. E_k=eU, U – ускоряющая разность пот-лов. λ_∂=2πћ/(корень 2m_eU), если U = 150 В, то _∂ = 1Ả. Такие решётки сделать нельзя, они  в природе – это кристаллы.

Опыт Тартаковского-Томсона: пучок эл-нов пропускался ч/з тонкую фольгу, наблюдалась дифракция на «объёмной» решётке, на экране – чередование светлых и тёмных колец. Эта картина такая же, если бы мы пропускали ч/з фольгу рентгеновские лучи с = 1Ả.

О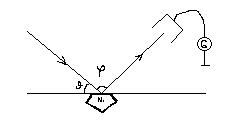 пыт Дэвиссона-Джермера (рис): дифракция наблюдалась в отражённом пучке эл-нов. Пучок направлялся на кристалл, отраж-ся, наблюд дифр на «простр-ой» решётке и на экране дифр картина, такая же как и с рентг лучами. Все опыты подтв-ли наличие волн св-в у микроч-ц, а значит правильность гипотезы. Меняли и φ => максим. ток набл. при φ=50⁰ и Е=54 эВ. 1) корпускулярная точка зрения . 2) Волн.т.зрения. Справедлива ф-ла Вульфа-Брегга

, d=0.91 - межплоскостное расст.

Несостоятельность взглядов: Правильн тракт-ку волнам де-Б дал в 1927 Бор. Если в кач-ве рабочего тела служит свет, то с волн т зр чередование max и min на экране опр-ся распредел-ем инт-ти волн, т.е квадратом её амплитуды, с корп т зр чередование опр-ся попаданием фотона в то или иное место экрана.

В 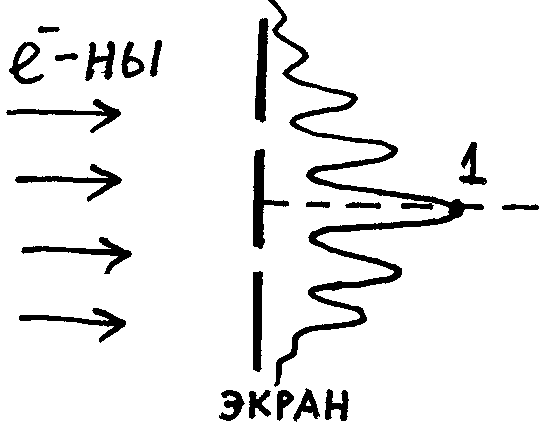олна ДеБ не может быть реальным волновым процессом. Если отождествлять её с реальной волной, то получим противоречие - такая волна занимает всё пространство, а частица – локальный объект.

Для главного MAX: I~|Ē₀|², N~|Ē₀|²W|Ē₀|² – вероятность попадания эл-на в т.1

Т.е волну деБр можно трактовать как волну вероятности, т.е величину

Ē(r¯,t)= Ē₀ exp i(k¯r¯- t)можно рассматривать не только как напряжённость поля волны, но и как некоторую функцию, вероятностным образом описывающую поведение соответственной микрочастичы.

41. Соотношение неопределённостей. ² общее соотношение непределённостей – устанавливает связь между минимальными значениями 2ух одновременно НЕизмеримых величин. Их неизмеримость означает: невозможность достоверного определения значений этих величин при измерении на опыте. При многократном повторении опыта по их измерению будет иметь место статистический разброс значений этих величин.

L^- оператор отклонения отсреднего значения. Пусть L=x, M=p_x, L^=x, M^= -i ђ·(∂/∂x). Вычислим

Поэтому [L^, M^]= iђ  [x^,p_x^]= iђ , (_x)² · (_p_x)² ђ²/4  _x_p ђ/2 _y_p ђ/2 _z_p ђ/2 – соотношение неопределённостей Гейзерберга. _x и _p – мера статистического разброса, а значит это точность измерения. Возьмем еще пару величин: Е и t. В качестве оп-ра берется t.

Выч-м коммутант:

=> чем дольше мы измеряем эн. тем точнее мы получим рез-т. Чем дольше тем меньше

_ E_t ђ/2 _t – промеж. времени, в теч. кот. произв-ся измерение эн-гии, _E – неопр-ть получ.результата.

Для атома: _t – среднее время жизни ат.в возб.сост., _E – неопределённость энергии фотона, излучённого при переходе атома из возб.состояния в основное

Физ. смысл: Чем с большей точностью мы измеряем (знаем)значение координаты, тем менее точно знаем импульс (и наоборот).

В момент просхождения через щель мы знаем “x” с определённой точностью – до ширины щели. Дифракция означает, что в момент пролёта через имеется импульс (_p_x ~L). Но опыт показывает, что при уменьшении _x увеличивается и размер главного максимума_p_x - увеличиваетсяч.т.д

Вследствие того, что нельзя абсолютно точно измерить координату и импульс одновременно, то в микромире координата задана только с определённой точностью траектория теряет смысл. В микромире также нарушается принцип причинности, т.е. в терминах координаты и импульса он не имеет смысла..

Принцип причинности в квант.механике: Временное Ур-ие Шрёдингера позволяет по известной начальной волновой ф-ции и хар-ру силового поля однозначно определить вид волны в  момент времени.

Спектральные линии: _E_t  ђ/2 - означает разброс значений энергии, измеренных в разное время.

Е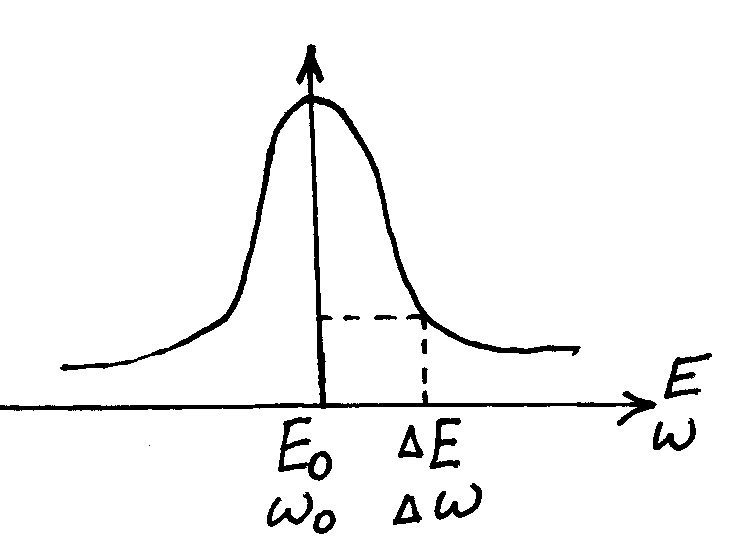 сли _t= (время жизни атома в возбужд.сост). то _E~ ђ/, хотя в каждом измерении энергия определяется точно.

_E – называется естественной (радиационной)шириной линии. Повторяя измерения многократно, мы получим целый спектр.

2.

42. Волновая функция: Приписав микрочастицам волновые свойства, деБройль сопоставил каждой частице ф-ию. координат и времени вида: ψ(r¯,t)= ψ₀ exp i(k¯r¯-  t), называемую волновой функцией. Такая ф-ция должна быть: - непрерывной; - конечной; - однозначной. Волновая ф-ция может не иметь волновой вид. Найдём вид этой ф-ции по времени t, это позволит определить её вид в  другой момент t+_t. Разложим в ряд Тэйлора: (1); (2); неизвестный оператор сдвига по времени, его вид постулируется. Оператор Подействуем этим оператором на ф-цию ψ: получим

; (3)- временное уравнение Шрёдингера, иначе (2*) ; Это урав-нение является основным в квант.мех-ке. Оно позволяет определить однозначно вид ψ, если известны – U(x,y,z,t), - ψ(r¯,0). Из-за волновых св микрочастиц вследствие соотношений неопределённостей в микромире нарушается принцип причинности. Т.к. при одинаковых условиях положение частицы можно определить только с опр.точностью. В квантовой механике временное уравнение Шрёдингера позволяет по известной начальной волновой функции и характеру силового поля однозначно определить вид волны в  момент времени.

Для стационарных полей U не зависит от времени  частное решение при U=UГ(r) примет вид для волновой функции (1*) показывает, что в стационарном силовом поле зависимость волновой функции от времени t имеет гармонический характер, причём хар-ер поляне важен. Фактически решение исходного ур-ия для стационарных полей сводится к решению уравнения :H^ψ(r)=Eψ(r) (4)

(1*) в (2*):

- ур-е Шр-ра для стац. состоян. или ; гам-ниан

Решая, мы находим ψ(r) и допустимые значения E=E_n. А поскольку ур-ие (4) – есть ур-ие нахождения собственных функций и собств значений оператора энергии, то найденные значения E_nдают допустимые значения энергии частиц: (5).

Физический смысл стационарных состояний (5):

1. это возможное состояние микрочастиц, находящихся в стационарном силовом поле.

2. это и есть состояния с опред.значением энергии, поскольку ψ_{n –} собств-ая функция оператора H^

3. вероятности измерения допустимых значений физических величин для частиц в сост.(5) не зависят от t

В силу последнего свойства эти состояния и наз-ся «стационарными» - это есть возможные состояния микрочастицы, находящейся в стационарном силовом поле, волновая ф-ция которой зависит от времени гармонически. Вероятности допустимых значений физич величин не зависят от времени. Энергии в этих состояниях имеет определённое значение.

43. Микрочастица в пот. яме с прямоуг. стенками: Одномерная глубокая пот. яма с прямоуг. стенками – это силовое поле вида U(x).

В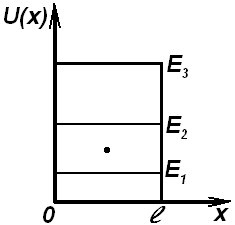 т. x=0, x=l пот.энергия не определена (=). Реально таких полей не , ч-ца внутри ямы 0<x<l.

У ч-цы 1 степ.свободы надо решить 1 ур-ие: Ĥψ=Eψ (2), где E – мех.энергия; ,(0<x<l); ,где граничн.усл: , ; ψ(0)=B=0B=0; , , т.о. (*), -энергия образует дискретный ряд собств. значений. . Из условий нормировки найдём: (ψ_n(x), ψ_n(x))=1;

(**)

А) Спектр частицы дискретный (из требования непр-ти волн.ф-ции); Б) (частица в яме не в состоянии покоя). Это согласуется с неопр-ми Гейзенберга:

_p·_x ~ ћ; _x ~ l, _p0 p0E0. Дискретность допустимых значений энергии связана с тем, что частица нах-ся в ограниченной области простр-ва. В) Прибольших n – дискретность: _E_n ~ 2n+1

Д искретн.спектр рассматр. как непрерывн при больших n.

(**) – даёт выражение для пространственной части волновых ф-ций стацио-нарных сост-ий частицы, нах-ся в яме. Т.е состояние, в кот.E имеет опр. значе-ния, описываемые (*).

Исходя из смысла волн.ф-ций мы можем определить распред.плотностей вероятн. простр-го местоположения ч-цы, нах-ся в том или ином стационарн. сост-ии. w_n=|ψ_n(x)|²

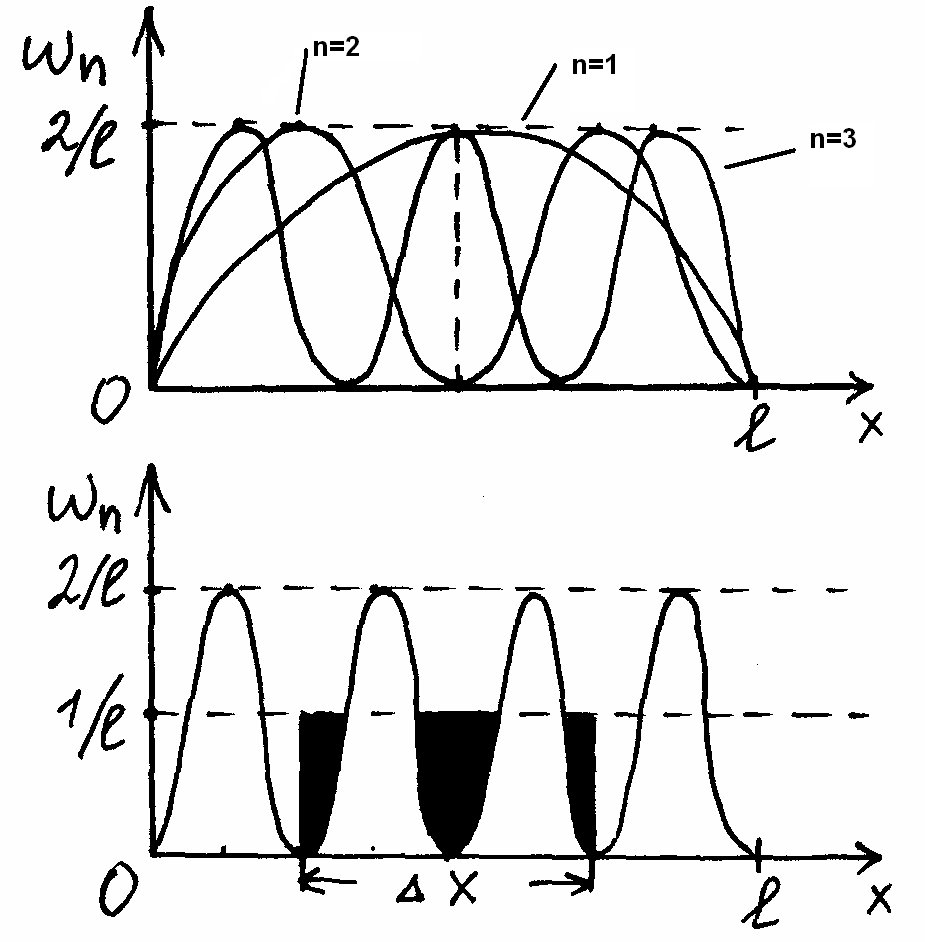
Точки, где волн. ф-ция обращается в 0, наз-ся узлами волновой ф-ции. При этом границы области узлами не являются. Этот результ. носит предельный хар-р(рис1). Если рассм-ть предельный случай n(рис2). 1/l – класс.распр.

Квант.распред переходитв класс-ое. С т.зр класс.теории ч-ца движется от стенки к стенке с пост. скор.плотн-ть вероятности опр.ч-цу: w_кл=1/l

ЛГО: В класс.физике ЛГО – это матер. точка, которая колеблется отн. положения равновесия по гармоническому з-ну под действием квазиупругой силы: F= –kx, F= –gradU; F= –dU/dx U=kx²/2; k=mω₀²U= (mω₀²x²)/2(*)

г 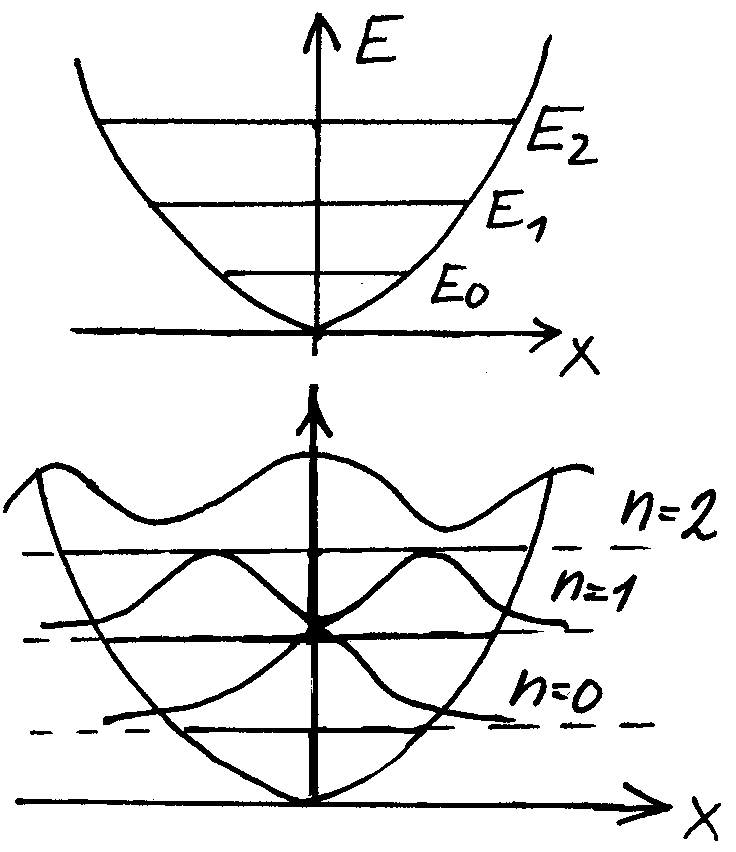де ω₀ – собственная частота колебаний.

В квант.физике ЛГО – это микроч-ца, наход-ся в потенц поле вида (*). Исслед-ие квЛГО сводится к реш.Ур-ия Шрёд.: Ĥψ=Eψ; Замена - размерность длины . , т.о . Далее делаем подстановку: ψ(ξ)= ψ(ξ)exp(-ξ²/2). Решение ищем в виде степенного ряда:

- рекуррентная формула для коэф. ряда.

Усл. разрыва ряда можно достичь произв. выбора λ: λ_n=2n+1, т.о E_n=ћω₀(n+1/2)Получим значение допустимых энергий квЛГО. Спектр этих значений явл. дискретнымПолученный результат соотв-ет гипотезе Планка. E=ћω₀·n, но Планк не учёл, что E_min0. Отличие от нуля говорит о недостижимости абс.0 температур.При больших n дискретность переходит в непрерывность.

44. Потенц-ый барьер : - область силового поля, в кот-ой потенц энергия частицы >, чем в соседних областях.

Р 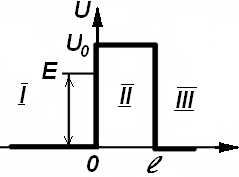ассм одномерный пот барьер прямоуг формы : Удобно разбить всю простр. обл-ть на 3 барьера.

Для I:

В класс. случае, если Е_К>U₀ – преодолеет барьер,

если Е_К<U₀ – не преодолеет (св-во непр. движ. класс.объ-ов)

В квант. случае: - переход из одного состояния в в др. осущ-ся дискретно – закон сохран. энерг. предполагает сохр-ие среднего значения эн-ии.

Решим стационарное ур-ие Шрёд-ра:

I: (x<0); II: (0<x<l); III: (x>l);

далее вместо µ писать æ!!!

где

Проанализируем решение для обл-ти I. Учтём зав-ть волн. ф-ции от времени. . Каждое из слагаемых описывает плоскую монохроматическую волну деБройля. Слагаемое B₁… распр в положит напр-ии, A₁ – наоборот (т.к kx-ωt=0, то x=(ω/k)t=υ_ср·t). В I имеет право  обе волны, в III может двигаться т-ко в положит напр-ии оси x, т.е от барьера A₃=0

Накладываем требования однозначности и конечности: Если потенц-ая энергия не испытывает скачков, то непрерывна 1ая производная волновой ф-ции.

,

Т.о. получим систему 4ёх Ур-ий, из которых находим:

- не понадобится; . B₃ находим из условия нормировки, на µ и к не накладываем ограничений. Спектр допустимых значений энергии ч-цы явл-ся непрерывным.

Вероятность прохождения ч-цей пот. барьера опр-ся величиной D= j_ПРОШ/ j_ПАД, где j – плотность потока, D – коэф. прозрачности. (коэфф. прохождения через барьер)

, , .

После преобразования получим:

. D0,

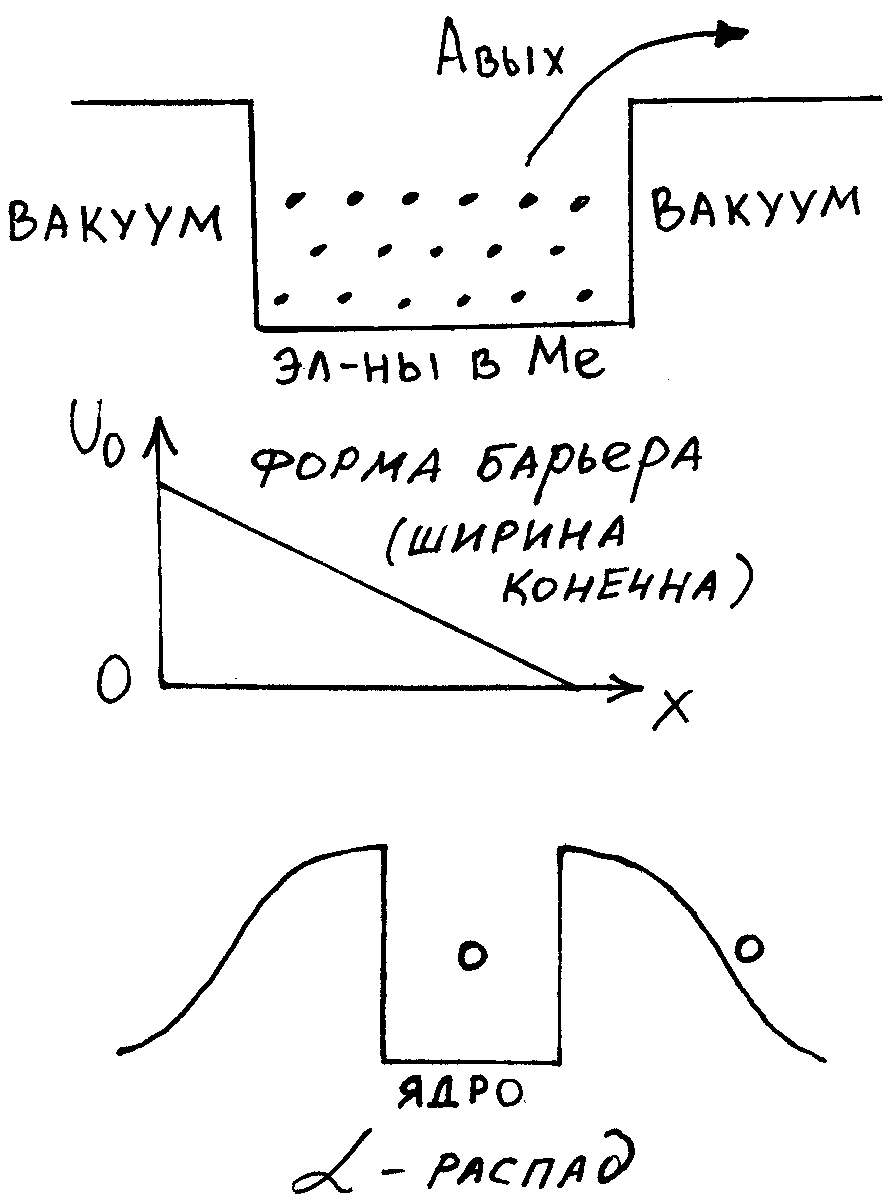
Физ. смысл: Есть вероятность 0,преодалеть барьер E<U₀ – это явление наз. туннельный эффект. Он объясн-ся природой микрочастиц и не противоречит з-ну сохр-ия эн-гии в квант.мех-ке.

Холодная эмиссия электронов из металла:

К металлу прикладывается сильное напряжение, U=U₀-eε x

Металл является катодом

α-распад:

Рассмотрим потенц. энергию α-частицы внутри ядра

Высота барьера – 20-30 МэВ

Энергия α-частицы~10 МэВ

45.Экспериментальные обоснования гипотезы спина: Квант. мех-ка на начальной стадии своего развития сталкивалась с трудностями при объяснении некоторых экспер. фактов.

1. Т 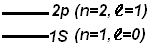онкая (мультиплетная стр-ра спектр-ых линий. Даже у одновалентных атомов стр-ра спектров оказалась сложнее, чем следовало из теории движения эл-на в поле центр.сил. Если взять атом Na, энергии зависят E_n,l. Переходу 2p↔1S – должна соответствовать 1 линия, а на опыте – 2 спектр.линии.

2 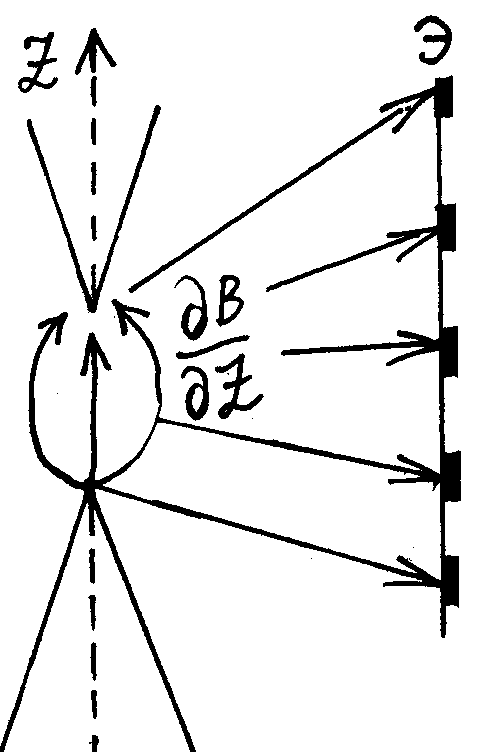) Опыты Штерна-Герлаха:

Как следовало из положений кв. мех. проекция магн. момента атома M_Z=m μ_Б. Цель опытов – проверить квантование магн.момента атома

Между полюсами спец. эл/магнита создавалось сильное неоднородное магнитное поле, поле напр-но вдоль Z, но сильно меняется от точки к точке, так, что ∂B/∂Z 0. Через это поле про-пуск-ся пучок эл-ов на экран. Во внешн/ поле действ.сила F^= –grad U U=-(M¯,B¯)= –M_ZB Если M_z не кван-ся, то на экране будет сплошное пятно, если кван-ся, то отдельные пятна (их число m=2l+1) Опыт это док-л, но кол-во пятен не совпадало, по теор их было больше.По опыту: пучок расщепляется на 2 это противоречило ранней кв мех.

3 ) Опыты Эйнштейна де-Гааза: Цель: проверить экспериментально гиромагнитное отношение g=M_z/L_z=e/2m_ec.. На тонкой кварцевой нити подвешивался стержень из ферромагн материала, вокруг была спираль по кот шел ток. Стержень намагничивался, возникало дополнительное магн. поле, напр-ое вдоль Z. Поле тока создаёт M_z, возникает дополнит. мех. момент.L_z-стержень начинает вращаться. Зная силу тока I, кол-во витков n и магн прониц-ть стержня μ м/о опред M_z, по углу закручивания . На опыте L_z. M_z/L_z=e/m_ec в 2 раза > чем в теории

Гипотеза спина: Чтобы объяснить эти и др. факты Уленбек и Гаудсмит (1925) выдвинули гипотезу спина.:

Помимо мех и магн момента (связ-го с вращ вокруг ядра) эл-он обладает собственным механическим и связанным с ним магнитным моментом. Собственный момент наз-ся спиновый мех (магн) момент – спин.,. Спин-ый момент может иметь 2 проекции относ орбит, им соотв 2 различ эн-ии взаим. Спин присущ не только эл-ну, но и др элем ч-цам. Спин – врождённая, фундам-ая хар-ка.

Надо приписать спинвому мом-ту значения S_Z=±ћ/2 , M_S – магн. спиновый момент, (M_s)_Z=±μ_Б=±eћ/2m_ec Объясним с помощью гипотезы спина опыты:

(3):Намагничивание стержня обусл-ся спином электрона, а орбит. момент  роли не играет, т.е Эйн&деГ. в опытах измерели гиромагнитное отношение для спина.(в ф-ле вместо L_z S_Z).

(2):Т.к у Эл-на помимо орбитального момента есть и спиновый, то понятно, что картина расщепления атомов будет иной, число полос будет больше, чем 2l+1. Тут надо говорить о полном моменте электрона, котор. складывается из орбит-го и спин-го. При l=0 у электрона остаётся спиновый момент. А т.к сп.мом может принимать 2 знач проекций на внешн.поле, атомы с l=0 должны расщепл-ся на 2 пучка – соотв-ие экспер-ту.

(1):Необходимо учитывать в/д спинового магнитного с орбит-ым магн. мом-ом. Т.е. в опер-ре H^ атома надо добавить член, соотв-ий этому в/д-ию - опер-ор возмущ-ия. Известно, что при наличии возмущения вырожденные эн.уровни расщепляются. Уровень 2p – вырожден и расщепляется на 2 уровня.

Операторы спина электрона:Требования для определения вида операторов спина (Ŝ_X, Ŝ_Y, Ŝ_Z): 1)операторы должны быть линейными, 2)эрмитовость, 3)матричные операторы размерность 2x2. Т.к. переем-ая Sz имеет дискрутный ряд значений 4) собственные значения операторов ±ћ/2, 5) (система (1)) Коммутационные соотношения для операторов (Ŝ_X, Ŝ_Y, Ŝ_Z) – операторы спина, должны иметь такой же вид, как для оп-ов L_x,y,z.

В ведём для вспомогат. целей матрицы кот-ые связаны с Ŝ_X, Ŝ_Y, Ŝ_Z:

, их собств. значения =±1; имеют собств. значения =1.Значит кажд. в своём собств.базисе имеет вид единичной м-цы (4)

Единичная м-ца в базисе остаётся неизменной , (4) справедливо в базисе.

В ычислим такую комбинацию:

Соотношения (4,5) можно объединить и предст. в форме:

Удовл-ие (6) матрицы 2x2 называются матрицами Паули,

а соотношение (6) – алгебра матриц Паули