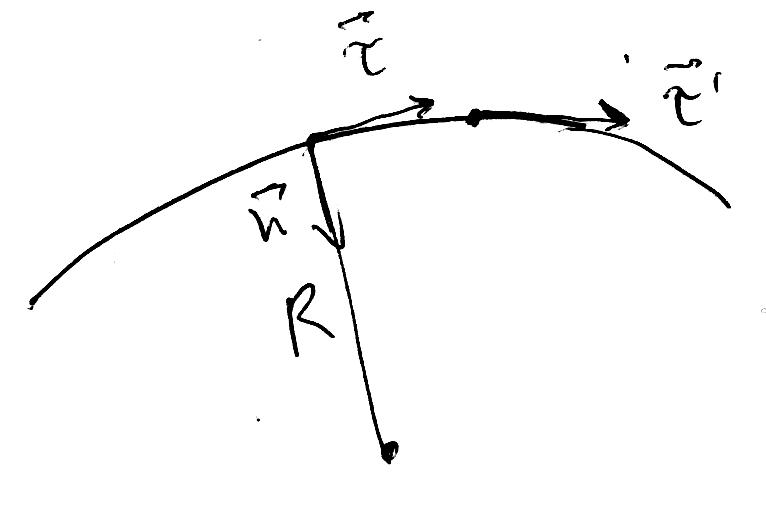1 . Мех. движение - перемещение тел или их частей относительно др. др. в течением времени. Сист отсчета - совокупность тела отсчета, связанная с ним сист коорд и набор инструментов для определения расстояния, углов, моментов и промежутков времени. Мат.точка – тело, размерами кот. можно пренебречь в усл данной задачи. Кинемат. ур-я движения: 1)Векторное (радиус –вектор данной точки); 2)Координатное сист ;3)Естественный (путь, коорд вдоль траектор). Радиус-вектор – вектор, соед-ий нач корд и мат тчк(телом). Перемещение – вектор, проведенный из нач корд в конечное положение тчк. Траектория – геометр-ое место концов рад-вектора мат тчк. Путь – расстояние пройденное мат тчк вдоль траектории. Скорость – физ (вектор) величина, хар-ая быстроту изменения рад-вектора с течением времени. Средняя векторная ск-ть : . Средняя скалярная ск-ть : . ! = => . Мгновенная ск-ть – производная рад –вектор по времени ( = ). Ускорение – физ величина, хар-ая быстроту изм ск-ти с течением времени. Среднее ускор: ; мгновенное ускор: = . Тангенс ускор: ; нормал ускор: ; ( ); полное ускорение: . Прямая задача кинематики: дано - r^→ = r^→(t), н-ти - v^→ и a^→, x=v₀*t+a*t²/2, v=v₀+a*t . Обратная задача кинематики: дано - a^→= a^→(t), н-ти - v^→=∫(от t₀ до t) (a^→*dt)=v^→(t)+C^→, r^→=∫(от t₀ до t) (v^→dt); Равномерное прям.движ.- движ., при кот.тело за  равные промеж. времени проходит равные пути. a=0, v=const, dx=v*dt, x=v*dt + C=v*t+C, при t=0 x=x₀, то C=x₀; x=x₀+v*t –кинематическое ур-ие движ. Равноуск. движ. – движ., при кот.ск-ть тела за  равные промежутки времени изменяется на одну и ту же вел: a=const, a=dv/dt, dv=a*dt, v=a*dt+C₁ = a*t+C₁, при t=0 v=v₀, то C₁=v₀, v=v₀+a*t; dx=v*dt, x=v*dt + C₂=v₀*dt+a*t*dt +C₂=v₀*t+a*t²/2+C₂, при t=0 x=x₀, то C₂=x₀, x=x₀+v₀*t+a*t²/2. a=(v-v₀)/t, x=x₀+(v-v₀)*t/2, t=(v-v₀)/a, x=x₀+(v²-v₀²)/2a. Принцип независимости движения: любое движ можно представить, как рез-т нескольких движ, происходящих независимо друг от друга. Физ-ая величина наз инв-ой относительно неких преобразований, если ее числовое зн-ие не изм-ся при этих преобразованиях координат. Закон движения наз инв-ым, если он имеет одинаковый вид в разных СО. Преобразования коорд: Поворот, Трансляция: ( -вектор трансляции) Простр-ая инверсия: Корд x скачком меняется на координату с против знаком

x’ = - x и т.д. Получаемые сист физ-ки равноправны, т.е. Ур-я в них сохран свою форму.Отражение времени: t=t’=-t В мех-ке это преобразование связ-т с применением уравнения дв-я к расчету полож-я частицы в … момент вращения

Основные св-ва:изотропия и однородность. Изотропия – позв-т повернуть СК как целое на произвольный угол вокруг любой оси, прох-ей ч/з начало корд-т. Однородность – позволяет сдвинуть СК как цеое наопред. расстоянте . Само преобразование – сдвиг (трансляция)

(2):выполняется при измен-и коордю осей на против-ные, либо при измен-и знака у коорд-т, опред-х данное мех событие в исх СК.

Преобразование Галилея: связь между коорд. тела в покоящихся и движущихся СК: (где = ), ,

Теорема Кориол.: Абсолютное ускор. равно сумме относит., переносного и кориол. ускор-й. .

2. Свободное – тело, движущееся равномерно и прямолин-но или покоящееся. Движ своб. тела наз движ по инерции. ИСО – такая СО, в которой все изол тела движ равн и прямолин или покоятся. 1-ый з. Ньютона: сущес-т такие СО, в кот. все свободные тела движ равн-но и прям-но или покоятся (или: сущ-ют ИСО). Инертность – способность тела препятствовать попыткам изменить его скорость. Масса – мера инертности. p^→ = m*v^→ - имп.тела или кол-во движ. Для изменения импульса необходимо воздействие на него др тел. Мерой такого воздействия является СИЛА. Сила – физ. вел, харак-я взаимод. тел в рез-те кот сами тела или их части преобретают ускорение. Принцип суперпозиции сил: уск. получаемое частицей при действии на нее нескольких сил, опред-ся геом суммой ускорений, получаемых частицей, при действии каждой из этих сил в отдельности. 2-й з. Ньютона: производная имп. по времени = приложенной силе. Основное Ур-ие динамики ч-цы: m*v^→=F^→. 3-й з. Ньютона: 2 матер точки взаимод-ют с силами, равными по величине и направленными в противоп-ые стороны вдоль одной прямой. Инвар-ть 2-го закона Н. т.е уск инвар-но отн ними, в системах О и О^/ можно записать: . Т.к масса частицы в классич. механике инвариантна, то Пр.относит. Галилея: Любые мех явления или процессы происходят в люб ИСО по одним и тем же законам, имеющим инвар-ю форму. Или: Никакими мех. опытами, проводимыми в рамках данной ИСО, нельзя обнаружить состояние движения отн др. ИСО. Исходной для мех-ки явл-ся сист мат точек в пустоте, связ-ых мгновенно передающ-ся взаимодействием. Силы вз-я между любым двумя частицами имеют центральный характер и подчин 3-ему з. Ньютона. Сила зависит от расстояния между частицами: F=F(r), а поскольку частицы могут двигаться, то F=F(r,t) В общем случае, F=F(r, t, v). Основные модели объектов и взаимод: 1) Классическая модель – все тела представл собой совокупность мат тчк, при этом если в-во распределено непрерывно, то за мат тчк принимается элемент объема dV. Сист мат тчк моделирует систему тел или одно протяженное тело. Для тел опр-мых в рамках этой модели предполагается св-во непроницаемости. Взаимод-ие между телами передается на расстоянии мгновенно (дальнодействие). Результат вз-ия состоит в непрерывном изменении импульса и кинетик св-в мат тчк. Тела относятся к макро миру и к области v<<c. Применимо к гравитацион и от части к эл магн взаимод .; 2)Полевая модель – применяется для изучения материи в виде макроскоп физ поля. Поле массой не обладает, т.е. не сводится к системе маттчк. Поле в пустом объеме без четких границ. Энергия в поле распростран непрерывно. Существует всего 2 макроскоп поля – гравитационное и Эл магн. Вз-ие осущ по средствам поля и передается с конечной скоростью (близкодействие). В результате вз-ия измен-ся характеристики тел и самого поля. Движение может быть как релятив, так и нерелятив.; 3)Квантово-релятивистская модель – применяется для изучения в макромире. Материя представлена элемента частицами, т.е. ч-ми малых размеров, к которым относятся элементы поля. Элементар ч-цы моделир точками, обладающие массой и энергией (микрочастицы). Взаимод-ие микрочастиц состоит в том, что они обмениваются квантами, при этом не только измен их движение, но и происходит взаимопревращ самих частиц. Силовое поле – область пространства, в каждой точке которой на част действует сила, зав-я от коор. и времени. Чтобы применять классич концепцию динамики, необх-мо чтобы время запаздывания стремилось к нулю, скорость взаимодействия C стрем к бескон. След-но v<<c. Границы: для макроскоипч. тел, v<<c

Равнод. сила : если речь идет о 1 частице, пожверж действию нескольких сил , то величина = сумме этих сил – равнодействующая.

m,a,F – инвариантны => II закон Ньют сохраняет форму во всех ИСО, но и связывает все инвариантные величины.

3. Осн ур-ие динамики частиц: , где - однозначная, конечная и непрерывная ф-ция, которая может быть определена независимо. Обратная задача: по заданным силам, действ-им на точку, определить закон ее движения. Дано: ; найти: ; необходимы нач усл : t = 0 , , . Алг решения: зная ,записываем: сист , , (Ньютоновская сист диф ур-ий). Общ решение: сист , , (1). Используем нач усл и получаем: сист , , (2). Дифф по времени: сист , , (3). (2) и (3) дают зак движ в виде 6-ти ур-ий: сист , .., (4). Подставляем (4) в (1) получаем: , , . Прямая задача: по известному закону движения тела определить равнодействующую всех сил, действ на тело. Дано: ; найти: . Алг решения: сист , , (1). С другой стороны: сист , , (2). Дифф (1) два раза по времени и подставляем в (2): , , (3). Использую (1) и (3) можно определить силовое поле. Принцип причинности в класс.мех-ке: знание ур-ия движ и нач усл позволяет полностью определить движ.мат.точки в  мом врем.( состояние системы материальных точек однозначно определяется их взаимодействием и начальными условиями.).Ур-ие движения в сист отсчета, произвол движ относ инерциал-ой: В общем случае система координат может быть связана с телом отсчета, движу­щимся произвольно в некоторой ИСО. Для записи уравнения движения частицы относи­тельно такой неинерциальной системы отсчета (НИСО) воспользуемся формулой сложе­ния ускорений (теоремой Кориолиса): . Умножая это равенство на массу частицы и учитывая, что - ускорение частицы в ИСО (т = ), получим: (*). Здесь сила выражает действие на частицу других тел и полей и может быть указа­на в виде функции координат, скорости и времени . Движение же НИСО проявилось в (*) через слагаемые и . Эти слагаемые кинетически в НИСО не могут быть обнаружены и интерпретируются как силы, приложенные к частице и вызывающие ее ускорение относительно НИСО. Т.о, чтобы сохра­нить для частицы в НИСО традиционную форму основного ур-ия динамики, величи­ны и следует рассматривать как особого рода силы - силы инерции, которые не являются результатом действия каких-либо тел или полей на частицу, а представляют прямой результат неинерциальности системы отсчета. Ур-ие движения в НИСО имеет вид: (**) Здесь -равнодействующая всех «ньютоновских» сил, действующих на частицу, переносная сила инерции, - кориолисова сила инерции (или просто сила Кориолиса).На по­коящиеся или движущиеся поступательно тела в НИСО не действует. Проявление сил инерции на Земле: Для тел на Земле центробежная сила инерции проявляется в зависимости ускорения свободного падения от широты местности (на экваторе величина g меньше, чем на полю­сах). Сила Кориолиса отклоняет движущиеся тела (в северном полушарии любая река больше подмывает правый берег; своеобразное движение маятника Фуко). Принципа эквивалентности сил инерции и гравитации: поле тяготения в небольшой области пространства и времени по своему действию тождественно действию сил инерции в ускоренной системе отсчета. Заметим, что в небольшой области пространства и времени гравитационное поле можно считать однородным и стационарным.

4. Механической системой наз совокупность мат тчк, выд-ую по какому-либо признаку.Центр инерции - воображаемая тчк, кото­рая как бы обладает массой всей системы, и положение которой определяется радиус- вектором , где и - масса и радиус-вектор i- й частицы. , . В ИСО величина, определяемая произведением массы частицы на ее ускорение, рав­на силе, приложенной к частице (второй закон Ньютона): , тогда , где -геометр сумма всех, сил действующих на частицу. Различают внутренние силы (действующие на данную частицу со стороны других частиц системы) и внешние силы (действующие на данную частицу со стороны тел, не входящих в систему). Геометрическая сумма внутренних сил равна нулю(III зак Ньютона). Дифф ур-ие движения: Движение системы из п частиц описывается системой п векторных (3п скалярных) дифференциальных уравнений: , i =1,2,..,n. Здесь силы являются известными ф-ми положений и скоростей частиц, а также време­ни. Если наряду с заданными силами на ч-цы системы дейст-ют силы, не извест­ные как ф-ции координат, скоростей и времени, то говорят, что на механическую систему наложены связи, (в общем) связи - ограничения, налагаемые на положения и скорости частиц механической системы. Геометрически ур-ия связей - уравнения поверхностей ( - удерживающая связь, частица движется по поверхности) или областей пространства, ограниченных поверхностями ( - неудерживающая связь, частица движется внутри поверхности). Голономными связи задаются алг ур-ями (или дифф ур-ями, сводимых к алг). Неголономные связи задаются дифф неинт-ыми ур-ями. Связь стационарная, если время не содержится в ее ур-нии в явном виде. Наложение связей уменьшает число степеней свободы системы: система из п частиц с т связями имеет s = 3n-m степеней свободы. Связь ограничивает и скорость частицы. Различают идеальные и неидеальные связи; при движении, ограниченном идеальны­ми связями, работа сил трения равна нулю. Действие связей сводится к силам, приложенным к частице. Принципом освобождаемости от связей :при известном ур-ии связи можно подобрать такую добавочную к заданным силу, которая влияет на движение частицы также, как и связь. Добавочные силы, заменяющие связи, называют реакциями связей. Они имеют одинаковую природу с заданными силами, но они возникают лишь при действии заданных сил или при движении тел. Примеры реакций связей: нормальная к поверхности реакция и касательная сила трения. Система дифф ур-ий движения: Задача о движении механической системы из п частиц с т голономными связями сводится к совместному решению дифференциальных уравнений движения и уравнений связей: сист , , , где i=1,2,..,n; k=1,2,..,m. Система (Зn + m) скалярных ур-ий содержит 6n неизвестных => задача не определена. Для систем с идеальными голономными связями можно записать еще (Зп - т) независимых соотношений между координатами частиц и реакциями связей, вытекающих из условия идеальности последних. Получим решаемую систе­му уравнений Лагранжа (первого рода).

В качестве основной аксиомы механики можно использовать принцип д'Аламбера-Лагранжа: в любой момент времени движения механической системы с идеальными связя­ми алгебраическая сумма виртуальных работ заданных сил и д'Аламберовых сил инерции равна нулю. Математ этот принцип выражает общее уравнение механики: . В обобщенных координатах (обобщенные координаты - независимые параметры, число которых равно числу s = 3n-m степеней свободы механической системы и через ко­торые однозначно выражаются все декартовы координаты частиц системы) общее уравне­ние механики преобразуется в систему уравнений Лагранжа (второго рода): , где k = 1,2 ,.., s, T-кин энергия мех сист, - обобщенные скорости, - обобщенные силы. Если силы обобщенно-потенциальные то можно ввести ф-цию Лагранжа , тогда ур-ие примет вид:

примет вид: . Уравнения движения мех системы, записанные в форме дифф ур-ий 1 по­рядка, наз каноническими уравнениями движения. Естественно считать независимыми переменными также и обобщенные скорости (или обобщенные импульсы ). Тогда уравнения Лагранжа для обобщенно-потенциальных сил имеют вид: . Вводя функцию Гамильтона (обобщенную энергию) и переходя от переменных к переменным , получим после преобразований канони­ческие уравнения Гамильтона: , . Существует ур-ие в частных производных, описывающее движение механической сис­темы в поле обобщенно-потенциальных сил при наличии голономных идеальных связей - уравнение Гамильтона-Якоби: , где - функция действия; при этом . Составление дифф ур-ий движения с помощью функции Лагранжа - формализм Лагранжа. В формализме Лагранжа независимы­ми переменными считаются обобщенные координаты и время. Метод составления дифф ур-ий движения для механических и других систем, основанный на использова­нии функции Гамильтона, называют гамильтоновым формализмом.

5 . Импульс – векторная величина, хар-щая движение тело, равная произведению массы тела m на его скорость . Для системы частиц(импульс равен геометрической сумме импульсов всех тел составляющих систему, или произведению масс всей сист на скорость ее центра масс (точка, положение которой хар-ет распределение масс в теле или мех сист)): . Теорема об изменении импульса: т.к , а по 2 зак Ньютона , , где , то получаем . Зак сохр-я импульса: в замкнутой сист (сист на которую не действуют внеш силы) геометр сумма импульсов тел, составляющих сист, остается постоянной при любых движениях и взаимодействиях тел системы. , т.е если F^→=0, то р-сохраняется. Следствие: 1)имп замк сист сохраняется, 2) центр масс замк.сист. движжется равномерно и прямолинейно или покоится. центр масс сист.частиц движется, как частица, масса кот.равна массе системы под дейсвием силы, равной главн.вект.внеш.сил системы. Момент имп.: L – вел, = векторному произведению рад.-вектора ч-цы на импульс: L^→ =[r^→p^→]; L^→ r^→; L^→ p^→; L=r*p*sin=p*h; [L]=1кг*м²/c. Для сист: . Теорема об изменение момента импульса: L^→=[r^→p^→] +[r^→p^→] = [r^→p^→] = [r^→F^→] = M^→ - главный вектор моментов внеш.сил. Закон сохр момента иимпульса: если M^→=о, то L^→=const. Интегралы движения - ф-ции незав-ых параметров, сохр-ющие свои значения при движении. Зав только от нач усл. Имеем 6 первых интегралов движения: 1) ; 2) ; 3) (это все из закона сохр импульса); 4) ; 5) ; 6) (все из зак сохр момента импульса). Д/у механики, осн-ые на зак Ньютона, приводят к первым интегралам движения или зак сохр-я энергии, импульса и момента импульса. Ур-е Лагранжа, осн-ое на применении обобщ координат, тоже приводит к законам сохранения обощ энергии и обобщ импульса. Обобщ импульс: . Тогда Ур-ие Лагранжа можно записать в виде: . Может оказаться, что L не зависит некоторых обобщ координат. Такие коорд наз циклическими: => => (закон сохран обобщен импульса). Однородность пространства: если все тела замк.сист.сместить в пространстве на одно и то же расстояние, сохранив при этом нач.усл.и дейст.силы, то это не скажется на дальнейшем развитии с-мы. Изотропия пространства: при повороте замкнут системы впространстве как единого целого с сохранением всех прочих условий, все процессы будут протекать одинакого. З-н сохр.имп.: q_k – обобщенная координата. При сдвиге q_k +∂q_k, ∂q_k = ∂q, L=L(q_k, q^_k, t); ∂L = (∂L/∂q_k)*∂ q_k-вариация, ∂L = (∂L/∂q_k)*∂q=0, ∂L/∂q_k = 0, тогда  p^_k = 0 и p = const. . З-н сохр.мом.имп.: если поворот. ф-ция Гамил-на Н=∑(к=1 до s)(∂L/∂q^●_k) q^●_k-L – обобщ эн-ия; dH/dt=-∂L/∂t – Ур-ние Лагр- з-н сохр обобщ эн.; p^_k=-∂L/∂q_k – з-н сохр имп.

6 . Если под действием силы изменяется абсол зн-ие скорости, то говорят, что сила совершает работу. Если скорость увел-ся, то работа силы положительная, иначе – отрицательная. Элементарной работой силы наз физ величина числена равная скалярному произведению силы на элементарное перемещение: , , , где - проекция на ось os. Тогда . Пусть =const, F=const => , [A]=1Дж=1Нм = 10⁷ эрг. Энергия – физ величина, мерой изменения которой явл работа. Рассмотрим одномерный случай: сила действующая вдоль оси OX, и движение происходит вдоль оси OX. Мат тчк массой m перемещается вдоль оси OX под действием силы F. . Умножим обе части на : ; => ; и обе части умножить на dt: Т.о. при смещении тчк на dx, сила совершает над ней работу , в результате чего изм-ся величина , хар-ая движение тела. Она наз кинетической энергией. Пусть тчк смещается из положения x1 в положение x2, а ее скорость при этом изм-ся от Vx1 до Vx2. Интегрируя получим: => - изменение кинет энергии частицы при ее перемещении равно работе, совершенной при этом силой. Кинетическая энергия системы частиц наз сумма кинет энергий ее частиц : . Для определения кин энергии сист частиц используют теорему Кёнинга: кинет энерг сист частиц равна сумме кин энергий ее центра масс (точка которая движется как центр масс системы, с массой равной массе всей системы) и кинет энергии частиц системы в СО, связанной с центром масс: . Консервативные силы («сохраняющие»). Если на тело действуют только консервативные силы, то его полная механическая энергия сохраняется. (это консервативные силы). Диссипативные силы – тождественно неконсервативные силы (силы трения). Пусть сила зависит от коорд и времени . Это неконсервативная сила. И пусть она удовлетворяет условию: , где , U –потенциальная функция. Полный дифф-ал: . Т.о. и U смысла энергии не имеет. Когда , то , и тогда U имеет смысл потенциальной энергии. Т.о. понятие потенциальной энергии имеет смысл только для поля консервативных сил. Потенциальная энергия – есть ф-ция от положения точки, grad от которой, взятый со знаком «-» равен силе, действующей на тело в данной точке. Потенциальная энергией системы частиц наз сумма потенциальных энергий частиц ее составляющих: . Полной механической энергией системы наз-ся сумма ее кинетической потенциальной энергий: . Полная механическая энергия системы (замкнутой и незамкнутой) сохр-ся в том случае, если на частицы системы действуют только консервативные силы. Обобщенная энергия: Перейдем к обобщ координатам. - ф-ция Гамильтона или обобщ энергия системы. Тогда ур-ие Лагранжа запишется в виде: . Закон сохранения обобщ энергии: если , то H=const. Если рассматреть случай консервативных сил, то H=T+U=E, т.е. если в системе действуют только консервативные силы, то обобщ энергия равна механической энергии. Однородность времени: все процессы в замкнутой системе, поставленной в разные моменты времени в одинаковые условия, протекают одинаково: => => H=const. Т.о. закон сохранения мех энергии для замкнутой системы и свободной от связей есть следствие ур-ний Лагранжа и однородности времени.

6(2)Пусть в системе действуют обобщенные силы: ,где -обобщенный потенциал. -ур-ие Лагранжа, где k=1,..,s. Умножим каждое ур-ие на обобщенную скорость и просуммируем: (1); = + (2). Подставим (1) в (2): (3) . (4); Тогда учитывая (4), (3)примет вид: . Обозначим функция Гамильтона обобщенная энергия сис-мы . Если функция Лагранжа явно от времени не зависит

4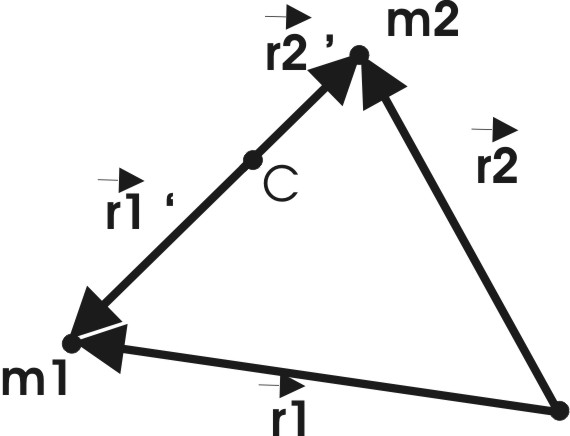 . Закон всемирного тяготения: две мат точки притягиваются друг к другу с силой пропорциональной их массе и обратно пропорциональной квадрату расстояния между ними. . Экспер-ми основания зак всемир тяг явл-ся законы Кеплера: I. Все планеты движутся вокруг солнца по эллиптическим орбитам, в одном из фокусов которого находится Солнце; II. Радиус-вектор планеты за любые равные промежутки времени покрывает равные площади; III. Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит. Из III зак Кеплера: , где [G]= . G – физическая величина, численно равная силе притяжения двух мат тчк единичной массы, нах-ся на ед расстоянии друг от друга. G=6.67^.10^-11 . Постоянная была определена на крутильных весах Кавендишем: легкое коромысло с 2 –мя шариками на концах , подвешенное на упругой нити, рядом с ними 2 неподвижных тяжелых шара. По углу закручивания опред-ось G. Жолли использовал обыкновенные рычажные весы. Гравитационное поле :  тело, имеющее массу, измеряемая работой, кот. соверш силы тяготения по перемещ тела единичной массы, создаёт вокруг себя в пространстве поле, кот действует на помещённые в него тела имеющие массу. Напряжённость - физ вел-на, числ. = силе действующее на единичную массу. Потенциал - физ вел-на измеряемая работой, кот совершают силы тяготения по перемещению тела единичной масссы из данной тчк в . . Теорема Остроградского-Гаусса: поток линий напр-ти гравитац поля через произв-ую замкн поверхность с точностью до пост-го множет-ля равен массе, нах-ся внутри данной пов-сти: ,где , ds – эл-ая площадка. Поток через эту площадку: ; => .Тогда 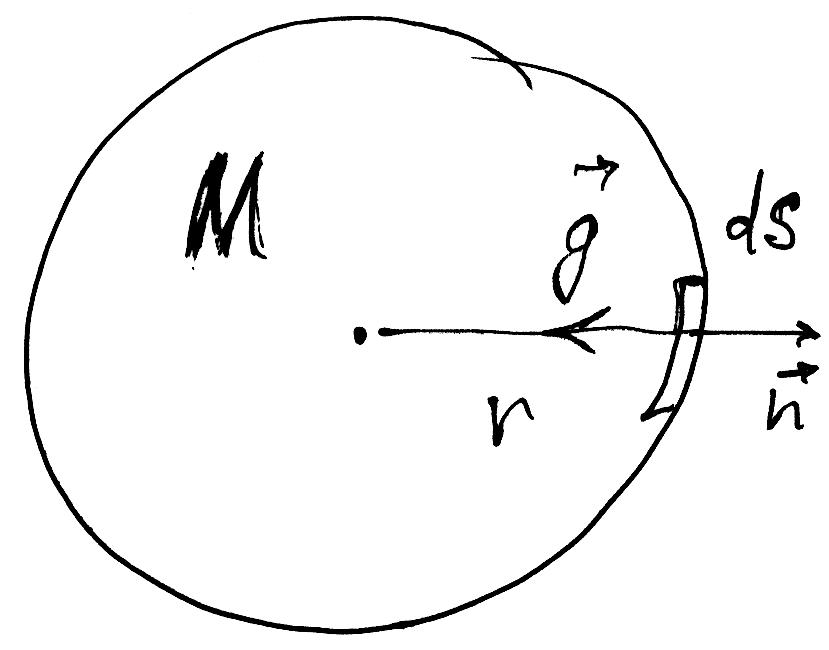Т.о. N не зав-ит от r и формы поверхности. Поток могут создать только источники, расположенные внутри поверхности. Задача: зная M, найти g внутри /снаружи /на поверхности шара. Найти соотв-ие потенциалы. Решение: , Радиус шара R. 1) r>R: => => ; 2) r<R: => ; 3) r=R: . Потенциал: => . Интегрируем: ; . На  => => . Вне шара: => .(r<R) . Задача двух тел: Имеется 2 тела m1 и m2. . По II зак Ньютона: (1)(для первого тела). (2)(для второго тела). Составляем сист из ур-ий (1) и (2). (1) делим на m1, (2) – на m2 и вычитаем из второго первое: или = . Пусть -приведенная масса. - свели задачу к решению ур-ия движения однородного тела с массой . Перейдем к СО, связанной с центром масс. и - радиус-векторы в СО центра масс. ; ; . Т.о. для системы с находим => и . Алгоритм общего решения задачи о движении частицы в центрально-симметричном поле: (1) – момент импульса в полярной сист коорд. Полная мех энергия: ; (2); ; - ур-ие показывает, что радиальную часть движения можно представить как движение в поле с эффект потенциал энергией: . При - тчк поворота. - инфинитное движение. - финитное движение. Существует 2 типа центр симетр полей, в которых все три фенитных … 7(2)…движения замкнуты: 1) ;2) . (из (2)); Помножим на r²: , где r – может принимать сколь угодно малые значения, если . Т.е. , либо как , где , либо , n>2. Задача Кеплера: поле притяжения кулоновского типа: . Находим траектории движения в дифф и интегральной формах: , , . ; . Находи - дифф ур-ие траектории, где , , . Используем понятие изобр-ей тчк, масса которой = приведенной массе: . Общее решение => - интегральное ур-ие тр-рии. . Если e<1 – эллиптическая орбита; e=0 – параболическая; e>1-гиперболическая. Формулы космических скоростей: 1 к.с. – скорость, которую надо сообщить телу у поверхности Земли, чтобы оно начало дваться по орбите: => ; 2 к.с. – для того, чтобы оно покинула Землю: => ; 3 к.с. – для, того чтобы оно покинуло солнечную систему: =>

5 Колеб-ние – это любой процесс, отлич-щийся той или иной степенью повторяемости. Гармонич. колеб.–это колебан при кот смещ-ние ч-цы от какого-то полож происх. по з-ну sin(a) или cos(a). Период – физ величина принимающая одно и тоже значение через одинаковые промежутки времени. Рассмотрим одномерный случай. Обобщ коорд q. Потенциальная энергия U=U(q)рассмотрим случай малых колебаний: => . Разложим вряд: . Можно считать . Условие равновесия: , . Тогда . Соотв-ая этой потенц-ой энергии потенц-ая сила: - квазиупругая сила, т.е. сила линейно зависящая сила от смещения и направлена противоположно смещению. Линейный гармонический осциллятор – простейшая модель колебательной системы. Можно лин гармон осцилл представить в виде пружинного маятника (жесткость пружины k). Квазиупругая сила – сила, величина которой пропорциональная отклонению от положения равновесия. Для данной модели: (сила Гука). Если k=const, то такая сила наз гармонической. Если же , то это ангармоническая сила. Ур-ие движения гармон осцилл: . Решение: , где А-амплитуда колебаний – максимальное смещение от положения равновесия. -фаза колебаний – угол, определяющий положение колеб-ся тела в произвольный момент времени. - начальная фаза. -циклическая частота или просто частота. Она не зависит от начальных условий движения и определяется свойствами системы. ; [ ]=рад/с; [ ]=1c^-1=1Гц. - период – время полного колебания. В общем случае кинетик энергия , где A(q)- постоянная или медленно меняющаяся ф-ция. Для малых смещений A(q)=m=const. Тогда ф-ция Лагранжа для одномерного осциллятора: . Подставляем в ур-ие Лагранжа и получаем : или , где , Легко проверить, что решение этого ур-ия явл-ся: , т.е. колебания являются гармон-ими. Т.о. вблизи положения равновесия сист совершает гармон колебания. 1) Для пружинного маятника: , где , k-жесткость пружины, m- масса груза. . 2)Для математического маятника(механическая система сост-ая из материальной тчк, подвешенной на невесомой нерастяжимой нити в поле тяжести): . 3) Физический маятник(твердое тело, которое может качаться вокруг неподвижной горизонтальной оси): где С-центр масс, А-ось вращения. Для малых колебаний . Решение: , где => , где -момент инерции. l=CA.

П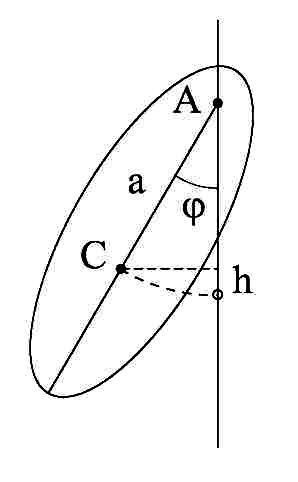 ри наличии сил вязкого трения (например, пружинный маятник в вязкой среде), кроме силы упругости : , дополнительно действует сила сопротивления, пропорциональная скорости: . Тогда: , где - диссипативный член. Обозначим , , получим: . Решение: , где , -амплитуда, зависит от времени. Для хар-ки затуханий вводят понятие логарифмический декремент затухания. - логарифм отношения амплитуд, стоящих друг от друга на период. , , - собственная частота. . Из формулы: видно, что амплитуда уменьшается в е раз за время -время релаксации. -коэф-т затухания. По другому: логар-ий декремент затухаяния: - величина, обратное числу колебании, по истечении которых А убывает в е раз. Пусть есть внешняя сила . Тогда по II зак Ньютона:…

8(2) … . Уравнение движения: (1), где , , . Амплиткда вынужденных колебаний измеряется по закону: , А=Аmax, при (2), где - частота собственных колебаний. Резонанс – явление резкого возрастания амплитуды вынужденных колебаний. Условие возникновения резонанс определяется ф-лой (2) . Решение ур-ия (1) имеет вид: , чтобы найти b и подставляем в ур-ие. Приравниваем коэф-8(2)…ты при cos и sin и получаем: сист. , . Откуда ; .Существуют колебания системы, в которых внешние воздействия сводятся к внутр параметрам самой системы. Колебания в таких системах наз параметрическими. Пусть (1), . Вид ф-ции , задается условиями задачи. Может быть периодической. Если это так, то (1) инвариантно преобразованиям . Тогда x(t) решение, и x(t+T) –тоже решение. Если x1(t) и x2(t) – независимые решения, то при замене они преобразуются друг через друга линейным образом. При этом можно выбрать x1 и x2 так, что изменения при преобразовании сводится к умножению по постоянным множителям: сист. , . Получаем, что пара коэфф и , совпадают с *и * (их комплексные сопряжения). Э.з., что либо = *, либо и -вещественные числа. Одна из этих ф-ций экспон-но растет современен. Э.з., что сост-ие покоя ситст при равновесии будет неустойчивым. Это есть параметрический резонанс. В отличии от обычного резонанса, когда , они остабтся равными нулю и в дальнейшем. Автоколеб. с-ма –колеб-я с-ма, кот. сама управляет поступлен. в неё энергии из вне. Амплитуда и период определяются свойствами системы. Для их поддержания система должна иметь источник энергии.

6. Гипотеза эфира: исходя из механических предст-ний, для объяснения распр-ния эл/магн волн предполагалось существование некоторой материальной среды, заполняющей все пр-во, в которой распр-ся эл/магн волны. Эту среду называли эфиром. СО связанная с эфиром наз абсолютной. Скорость тел отн-но данной ИСО тоже наз абсолютной. Скорость света отн-но эфира постоянна во всех направлениях и равна с. Но эл/магн волны это поперечные волны, поэтому это вело к наличию свойств твердого тела у эфира. Т. к. эфир – твердое тело, то он должен обладать массой и взаимод-ть с др телами имеющими массу. Опыты это не подтверждают. И не понятно. почему наряду с поперечными волнами в эфире не распр-тся продольные. 1)Наблюдения Брадлея: 18в, открыл явление абберации (если наблюдать свет из разных ИСО, движ-ся друг относительно друга, то он будет наблюдаться в различных ИСО под разными углами относительного общего для всех ИСО направления). В пределах одной ИСО обнаружить абберацию невозможно, но Земля раз в полгода переходит из одной ИСО в другую, при этом видимое направление на какую-то звезду изменяется. Т.о. в течении года она описывает абберационный эллипс. Абберацию можно объяснить, если считать эфир неподвижным. 2)Опыты Майкельсона и Морли: источник света, полупрозрачная пластинка, зрительная труба, 2 зеркала. Пройдя через полупрозрач пластинку луч делится на 2, между которыми образуются разность хода t и в трубе возникает интерференционная картина. При повороте установки на 90 ^о должна возникать некоторая разн-ть хода t' и интерференционная картина должна смещаться, но на опыте это не подтверждается. Эффект движения Земли отн-но эфира не был замечен. Оп. Физо: Физо заставил интерферировать лучи света, проходящие по и против течения жидкости. Согласно классическому закону сложения скор-тей интерференц. картина должна была смещаться согл. изменению скор. u=c/n±. Физо получ-л закон смещения полос: u=c/n±(1-1/n²), => эфир частично увлекается движущейся средой =>закон сложения скор-тей отличен от класс. Т.о. видно что при объясн-ии результатов всех 3-х опытов возникают противоречия, которые не могут быть разрешены в рамках теории эфира и классической физики. Принцип отн-ти Эйнштейна: при одинаковых условиях и одинаковых начальных данных все физические явл-ия протекают одинаково во всех ИСО. или Никакими физическими опытами нельзя обнаружить состояние движения одной ИСО относительно другого. Постулат о постоянстве скор. света: Скорость света в вакууме постоянна во всех ИСО во всех направлениях, равна с=3*10⁸ м/с, является mах из всех возможных скор-тей. В классической механике и преобразованиях Галилея часы во всех СО идут одинаково (сигнал передаётся мгновенно), а Эйнштейн вводит постулат о постоянстве скорости света, т. е. время в разных СО течёт по разному. Преобразования Лоренца: Из постулатов теории относительности вытекает, что преобразования Галилея с ними несовместимы. Получим преобразования, совместимые с постулатами СТО: Пусть К’ движется относительно К вдоль оси x со скоростью , тогда . Считая, что пространство однородно, время однородно. Тогда искомое преобразование должно быть линейным. Сист. , , , . Получены Лоренцам в 1904г. (еще до создания СТО). При преобразования Лоренца переходят в преобразования Галилиея классической механики. 1) Замедление времени: В рамках СТО понятие одновременности двух событий не является абсолютным. Пусть в К два события: и . В K’ : и . Составляем разность , получаем: - самая общая формула, связующая промежутки времени между двумя событиями, произошедших в разные моменты времени и в разных тчк. Пусть , . Т.е. в К’ эти два события произошли в одной и той же точке => . Видно, что при и . Это и есть ф-ла замедления времени. - собственное время – измеряемое в СО, связанной с часами. Всегда . Замедление времени обусловлено разным способом отсчета времени в разных ИСО: измеряется одними и теми же часами, расположенными в одной и той же ИСО, измеряется двумя часами, расположенными в разных пространственных тчк. Сокращение масштабов: Пусть в К’ покоится стержень длиной . Координаты конца и начала x2’ и x1’ измеряются одновременно в K’. Пусть K’ движется относительно К стандартным образом. В К координаты конца и начал также измеряются одновременно: x1 и x2. Из преобразований Лоренца вытекает: и . ; => ,где -собственная длигна – длина стерж в той СО, в кот он покоится . Видно, что в отличие от классик физики, длина жесткого стержня неивариантна, а зависит от координат СО, в которой происходит измерение. Максимальную длину она имее в той ИСО, относительно которой оно покоится. Релятивистская формула сложения скоростей: Пусть К’ движется о тносительно К стандартного образом. В К’ движется частица. Проекции ее скорости в этих СО: и . Т.к. ф-лы преобразования Лоренца 9(2) справедливы и для бесконечно малых величин, то: (1); (2); (3); (4). Разделим (1) на (4): (5). Разделив (2) и (3) на (4): ; (6). Видно, что (5) и (6) несимметричны, т.к. движение происходит стандартным образом. Если частица движется вдоль оси X: . Видно, что даже в предельном случае, когда с есть скорость K’ относительно К или скорость материального объекта равна скорости света, все равно .

Т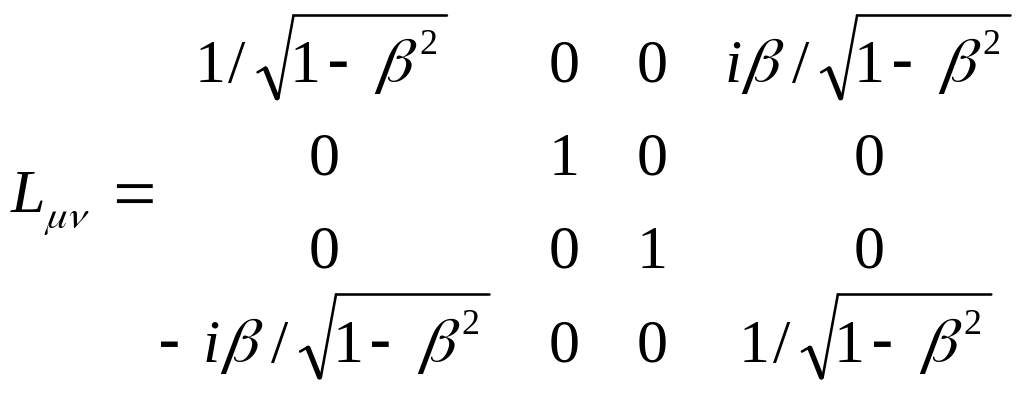 .к. в рамках СТО пространственные и временные координаты неразрывно связаны друг с другом, то стоит говорить об едином 4-х мерном однообразии - 4-х мерном пространстве времени. Это пространство – пространство минковского. . Тогда преобразование Лоренца: , где - индекс суммирования, - свободный индекс. = 1,2,3,4. -матрица Лоренца. Т.к. преобразование Лоренца является математическим выражением принципа относительности Эйнштейна и постулата о постоянстве скорости света, то принцип относительности можно сформулировать так: законы природы должны быть инвариантными относительно преобразований Лоренца. Действительно, если какой-то закон неинвариантен относительно преобразований Лоренца, то он по-разному формируется в различных ИСО. А это значит, что различные ИСО неинвариантны.

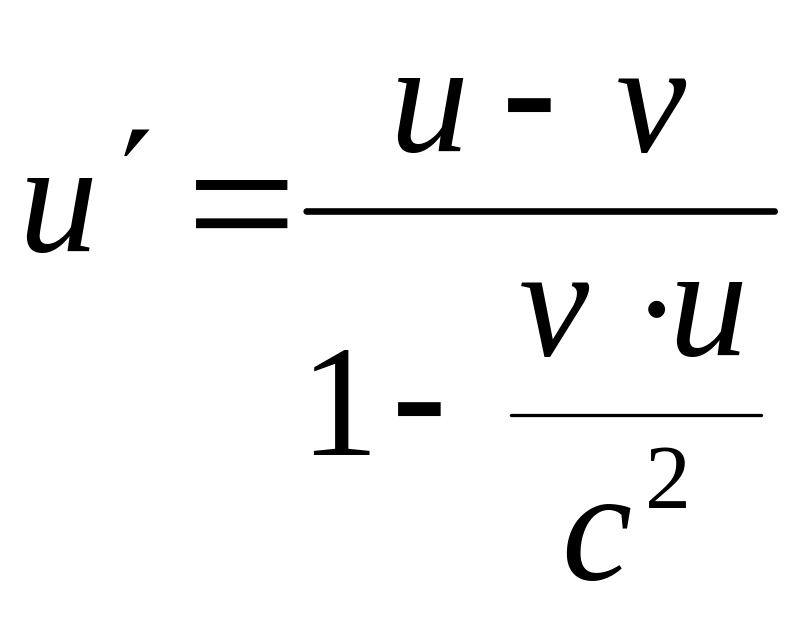
7. З-ны, кот форм-ся одинаково во всех ИСО – релят инв-ные. Если з-н правильный, то он д. б. рел-ки инвар-м. Это и есть: треб-ие инв-ти з-ов природы. Треб-ие имеет больш. эврист. ценность.

А) з-ны:прав-ые и неправ-ые; б) строя нов. з-н следует проверять теорию на треб-ие релят. инвариантн. Предъявл. усл.: уравнение надо сразу зап-ть в такой форме, что бы инвар-тьз-на была очевидной, чтобы проверить ничего не надо. Такая форма записи – ковариантная.

2 зак Ньютона , где -масса частицы. В классической механике она инвариантна, т.е. совпадает с массой частицы в ИСО где она покоится. В другой форме . В таком виде второй закон Ньютона неинвариантен относительно преобразований Лоренца (Сист. , , , ), т.е. не соответствует постулатам Эйнштейна(при одинаковых условиях и одинаковых начальных данных все физические явл-ия протекают одинаково во всех ИСО. или Никакими физическими опытами нельзя обнаружить состояние движения одной ИСО относительно другого.): т.к. классическое ур-ие движения включает в себя инвариантную массу, которая не зависит от скорости движения то действуя на частицу силой любой величины, ее можно разогнать до скорости . А это противоречит постулату о постоянстве скорости света (Скорость света в вакууме постоянна во всех ИСО во всех направлениях, равна с=3*10⁸ м/с, является mах из всех возможных скор-тей.). Ур-ие движения должно имеет квантовый вид. 3-х мерное ур-ие движения: или , , , где m – релятивистская масса, - масса покоя. Релятивистская масса также как и нерелятивистская характеризует инертность частиц. Смысл зависимости массы от скорости заключается в том, что в релятивистском случае отношение не является постоянным, а зависит от скорости. Например для заряженной элементарной частицы в эл магн поле: ; , константой является масса покоя -мера инертности при нулевой скорости. Кроме того, в релятивистском случае направление ускорения и силы не совпадают.

, -эн покоя, -1)- кин энергия . . . . . Закон сохр-я эн: полн-я релят энер-я изол-й сист. сохр-ся

Формула связи между полной релятивистской энергией и массой: , где . Эта формула связывает две важнейшие характеристики материи: энергию и инертность, т.е. массу. Приведенное соотношение показывает, что оно справедливо как соотношение между инертной массой частиц и ее полной энергией. Эксперимент показывает, что оно справедливо не только для суммы кинетических энергии и энергии покоя, но и для любых видов энергии. Физический смысл соотношения: можно сформулировать так: какие бы взаимопревращения форм энергии и массы ни происходили в природе, между ними всегда существует это соотношение. Зависимость вынуждает отказаться от определения массы как количества вещества. Существуют материальные объекты с нулевой массой покоя. Например фотоны: , но их энергия , импульс: . Связь энергии и импульса: . Для частиц с ненулевой массой покоя легко получить связь полной энергии и импульса: Знаем: , где ; импульс . Тогда , добавляем к обеим частям слагаемое : = …= . Т.о. или .

Переходим к 4-ч мерным координатам: . Следовательно проекция 4-х мерной скороти: , , , . ;-ч мерный импульс имеет следующие проекции: , где . Преобразования Лагранжа в 4-х мерной форме: . Инвариантом относительно преобразований Лагранжа является квадрат 4-х мерного вектора, т.е. можно показать, что (1). Имея проекции 4-х мерного импульса: ; ; ; и принимая во внимание (1) получаем: . Пусть частица покоиться: , . Тогда => => . Имея 4-ч мерный импульс, можно записать релятивистское ур-ие движения в ковариантной форме: , где -дифф-ал собственного времени частицы ( ) , -4-х мерная сила.

8. Основные положения МКТ:1.Полная хаотичность движения;2.Средняя скорость движения молекул газа прямопропорциональна корню квадратному из абсолютной температуры( ). 3.Средние кинетически энергии разных газов при одинаковой температуре равны между собой( ). Опыты Броуна: Положение 1. установлено на опытах в 1927.Он фиксировал положение спор папоротника ч/з. равные промежутки ∆t. Врезульт. Получил ломаную линию. Если уменьшать ∆t, то получим опять ломаную линию. Теор.оъясн.была дано в 1905 Эйнштейном(независ. Смолуховским). Эйнштейн ввел понятие флуктуации. Ф. наз. случайное отклонение физ. величины от среднего значения. Ф. наблюдаются для малых промежутков времени и малых размеров. Число ударов молекул жидкости, в которой взвешена бр. частица, может отклонятся от среднего значения.В опр. мом. времени число ударов слева больше чем справа, вследствие чего появл. результир. сила, перемещающая бр. частицу. Опыты Штерна: Положение 2. установлено на опытах в 1920. Имеется 2 коаксиальных цилиндра. внутри которых платиновая нить покрытая серебром. Внутри высокий вакуум. Пропуская ток ч/з проволоку, разогревают ее, при Т=1200К, атома серебра отрываются от проволоки и пролетая ч/з диафрагму D, осаждаются на вн. поверхности большого цилиндра вдоль линии. При вращении место осаждения сместитсяв положение B. r<<R→время пролета ∆t=R/с, ∆S=ωR∆t→ . Изменяя величину тока, Штерн увелич. T и получил: . Размытость линий-молекулы летят с ралич. скоростями. -основное ур-е МКТ. Равновесное состояние системы- состояние, в котором все параметры системы имеют определенные значения, остающиеся при неизменных внеш. условиях постоянными сколь угодно долго.

Осн ур-е МКТ. Ид-ный газ – это модель реального газа, в кот. пренебрегают размерами молекул, т.е. считают их материальными точками, и считают, что мол-лы взаимод-ют только при ударе и удар считается абсолютно упругим. Рассм однор. идеал. газ, масса каждой молек.-m₀N-число молек. газа, который нах. в сферич. сосуде радиусом R. Цель: н-ти P данного газа на стенки сосуда. Будем считать, что молек. не соуд-ся м-у собой, т.е. газ разряжен. Выделим отдельную молек. со ско-тью V_i . Пусть она удар-ся в т-ке А под углом  к нормали, после чего она отскоч. со ско-тью V_i по абсол велич под углом . Найдем изменение кол-ва движ-я при единичном ударе. ∆K^→_i=K^→_2i - K^→_1i, из ∆ АОB)получаем, что │∆K_i│=2m₀V_icosφ .Время полета м-у двумя соудар-ми: t=AB/V_i (1);из ∆ ОBА получ. что AB=2Rcos (2); подставляя (2) в (1) получаем t=(2Rcos)/V_i . Число ударов в един. времени =1/t=V_i /2Rcos . Изменение кол-ва движ. одной молек. за един. времени ∆К_i¹=│∆K_i│; ∆К_i¹=(2m₀V_icosV_i)/2Rcos=(m₀V_i²)/R; Тогда импульс, кот. получит стенка со стороны всех частиц ∆K¹=∆K_i¹=(m₀V_i²)/R (3) . Средн квадр ско-ть: с²=(V_i²)/N (4); подставляя (4) в (3) получ. ∆K¹=(m₀Nc²)/R ; Далее воспольз. 2-ым з.Ньют.: ∆K¹=F∆t; и положим, что ∆t=1с, тогда F=(m₀Nc²)/R ; Давление расч-ся поф-ле: P=F/S=F/(4R²)=(m₀Nc²)/(4R³) (5) . Домножим и раздел. (5) на 3. В знаменателе получ. объем сферы. Т. обр. из (5) получ. PV=(Nm₀c²)/3 (6) - Осн ур-е МКТ. Основ достоинство данного ур-я состоит в том, что оно связывает макроскоп параметры газа PV с микро параметрами отдельной молек m₀ и c². Это уравнение мы получ для разреж газа, но результат можно обобщить для плотного газа. В этом случае выбранная молек. прежде чем долететь до т.А испытает большое число соударений. Однако т.к. молекул очень много то в т-ке А всегда найдется молек, к-ая испыт соудар согласно нашей схемы. Т.обр. ф-ла (6) применима и для плотного газа домнож и разд (6) на 2, тогда получ. P=(2nE)/3 (7) , n=N/V-конц.; E=(m₀c²)/2-ср.кин. эн. пост. дв. мол-л газа. Физ. смысл (7): Давление с точностью до пост множителя опред-тся средн кинет энергией поступательн движения молекул газа в единице объема.

8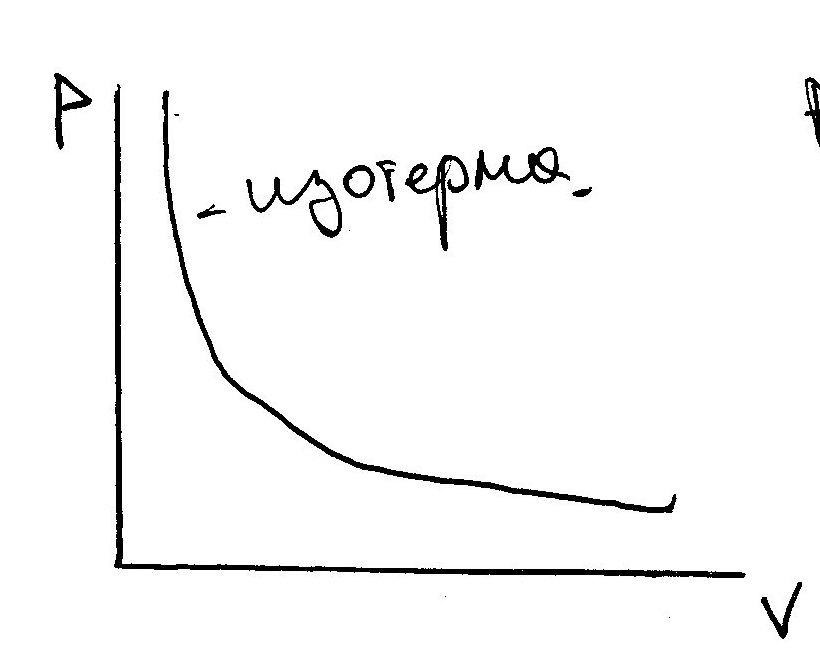 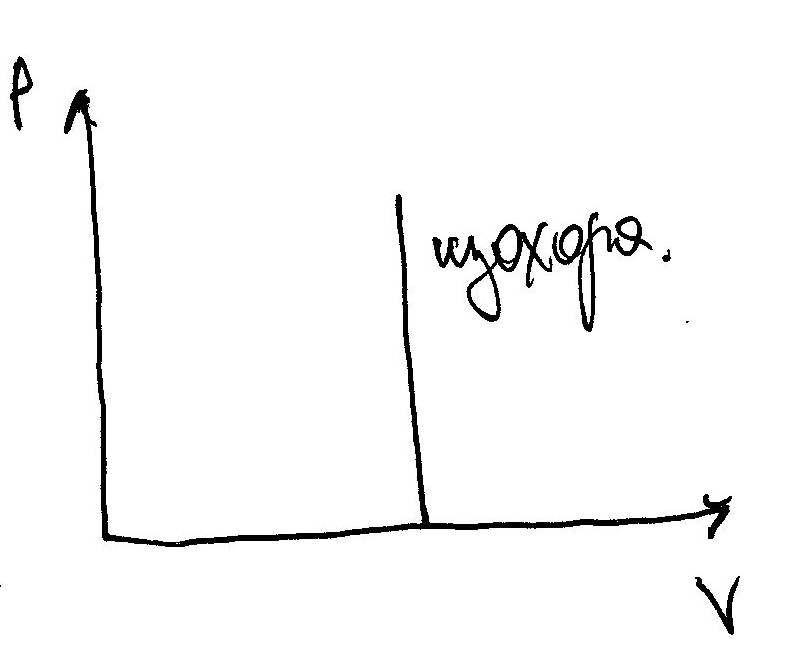. PV=(Nm_oc²)/3 (1); 1.Закон Бойля-Мариотта(изотерма рис.1): для данной массы газа при T-const произвед. давления на объем есть величина постоянная. PV=const; Для того, чтобы вывести этот з-н, воспольз. 2-ым осн-ным положением МКТ: средняя ск-ть газовых молекул пропорциональна корню квадр. из темп-ры: c~(T)^1/2 или c²=aT (2) ; где а – кооэф-нт пропорц-ти. Запишем (1) используя (2) для 2-ух последовательных состояний: P₁V₁=(Nm₀aT)/3; P₂V₂=(Nm₀aT)/3; Из последн. с-мы ур-ний следует: P₁V₁=P₂V₂. 2.Закон Шарля(изохора рис.2): для данной массы газа при V-const давления относятся, как абсолютные темпер-ры. Запишем (1) используя (2) для 2-ух последовательных состояний: P₁V=(Nm₀аT₁)/3 ; P₂V=(Nm₀аT₂)/3 : P₁/P₂=T₁/T₂. 3.Закон Гей-Люсака(изобара рис.3): для данной массы газа при P-const объемы относ-тся как абсолют темпер-ры. Запишем (1) используя (2) для 2-ух последовательных состояний: PV₁=(Nm₀аT₁)/3 ; PV₂=(Nm₀аT₂)/3 ; V₁/V₂=T₁/T_2. 4.Объеден газовый закон: для данной массы газа произведение давления на объем деленное на темп-ру есть величина постоянная. PV/T=const; Запишем (1) используя (2) для 2-ух последовательных состояний сохраняя только массу: P₁V₁=(Nm₀аT₁)/3 ; P₂V₂=(Nm₀аT₂)/3 ; Из последн. с-мы ур-ний следует: P₁V₁/T₁=P₂V₂/T₂. 5.Закон Дальтона: давление смеси газов=сумме порциальных давлений. P=P₁+P₂+…P_k . Парциальное давл-это давл одной компоненты смеси при усл-и отсутствия всех остальных компонент. Для получения этого з-на восп-ся осн. ур. МКТ в виде: P=(2nE)/3 (3) . E-сред кинет энергия 1 молекулы, n-концент. смеси: n=n₁+n₂+…n_k Далее восп-ся 3-им осн. положен. МКТ: средние кин-кие эн-гии молекул разных газов при одинаковой темп-ре равны: E₁=E₂=…=E_k Подставляя все в (3) получим: P=(2n₁E₁ )/3+(2n₂E₂)/3+… что и т. д. 6.Закон Авагадро: в одинаковых объемах разных газов при равных значениях P и T наход-тся одинак кол-во молекул: N₁=N₂; Т.к. тем-ры одинаковы, то согласно 3-му пол-нию МКТ : (m₁c₁²)/2=(m₂c₂²)/2 ; Тогда осн. ур. МКТ для 2-ух состояний им. вид: PV=(2N₁(m₁c₁²)/2)/3 ; PV=(2N₂(m₂c₂²)/2)/3 ; откуда следует, что N₁=N₂. Физ смысл Т: Средняя кин. эн. частицы опр-ся по ф-ле: E=(3kT)/2 из кот-ой и вытекает физ. смысл т-ры: Темпер-ра с точностью до пост. множит. опред. средн кинет энерг 1 молекулы. Понятие «средн кинет энерг» 1 имеет принципиальное значение.. Темпер-это сво-во сугубо макроск сист, т.к темпер. явл. энергит хар-ой сист, то измер ее можно в единиц энергии. Физич парам-р, одинак-ый во всех частях сист тел, наход-хся в сост-нии теплов равнов-сия, наз темпер-рой тела. Абсолют ноль - это темпер-ра, при к-ой прекращ-тся всякое тепловое движ-е молекул газа.(или состояние при котором средн кинет энерг молек =0.) Принцип недостиж абсол 0: абсол ноль недостижим. Найд-м связь м-у абсол шкалой и шкалой Цельсия. Для этого воспол. газов термометром, в кот. термометрической вел-ной явл. давл., а термометр-им телом – ид. газ. Т.обр. можем воспольз. з-ном Шарля: P₁/P₂=T₁/T₂. Помещаем газ поочередно в тающий лед и кипящую воду. При помощи барометра экспер. опред P_k/P_п=1.3661; Согласно з. Шарля таким же должно быть отношение температур: T_k/T_п=1.3661 (4) (п-точка плавления льда); Чтобы градус абс-ной шкалы совпадал с гр. Цельсия весь интервал от кипения воды до плавления льда разобьем на сто частей: T_k-T_п=100 (5); Решая с-му (4) (5), получим T_п=273.15К ; T_k=375.15К; т.к. t_п=0 по Цельсию, то получаем T=273.15+t.

Рассм. каноническое распределение Гиббса: . где p-обобщенный импульс, q-обобщенная координата. Покажем ,что θ-стат. аналог термодин. абс. температуры. Необходимо доказать:1.2-системы с одинак. знач. θ находятся в равновесии между собой;2. 1/θ-интегрируемый множитель для элемента кол-ва теплоты δQ. 1. Пусть имеется 2 равновесных термодин. системы: ω(p₁,q₁) и ω(p₂,q₂). Если привести систему в контакт, то благодаря взаимодействию между ними, начнется переход энергии, ноЕ₁+ Е₂=Е=const.Тогда функция для объед. системы имеет вид: ω(p₁,p₂,q₁, q₂)= ω(p₁,q₁) ω(p₂,q₂)=exp{(F₁/θ₁+ F₂/θ₂)-( E₁/θ₁+ E₂/θ₂)}. Если объед. система наход. в равновесии, то для ее: …

… → , → . Система окажется в равновесии, если θ₁=θ₂. 2. Докажем второе утверждение используя 2-ое нач. термодинамики: δQ=dU+∑a_kdβ_к, где , ∫exp(F-E)/θdpdq=1-условие

13 Уравнением состояния наз. ур-е, которое связывает воедино параметры состояния системы. Состояние идеального газа характеризуют P,V,T. Для получения ур-я состояния воспользуемся объединенным газовым законом: PV/T=const. Запишем данный закон для единицы массы вещества: PV/T=B.Полученное ур-е PV=BT- не является универсальным, т.к. B-const для каждого газа имеет свое значение(PV=BT-ур-е Клапейрона). Менделеев усовершенствовал это ур-е, воспользовавшись опытным фактом: 1 моль при нормальных условиях занимает объем V₀= 22,4 л, при P₀=1,01*10⁵ Па, T₀=273 K. Запищим ур-е Клапейрона для одного моля газа: PV/T= P₀V₀/ T₀. Вычислим B:B=8,31(Дж/мольК)-универсальная газовая постоянная. С учетом полученного значения, имеем:PV=RT-ур-е Менделеева-Клапейрона. Запишем данное ур-е для произвольной массы. Мы имеем ν моль, тогда при нормальных условиях данный газ занимает объем νV₀. Подставляем в ур-е: PV= νRT, где ν=m/μ. PV= m/μRT.

Средняя квадратичная скорость –отражает скорость коллектива молекул в целом.

, известно, что молекулы в газе распределены по скоростям. Согласно 2-му положению МКТ, с-√Т →с²-аТ. Найдем константу а. Для этого воспользуемся осн. ур-м. МКТ и ур-м состояния для одного моля: PV=1/3N_Am₀c² и PV=RT.→ 1/3N_Am₀c²= RT→ c²=3RT/ N_Am₀, где R/N_A=κ-постоянная Больцмана.→ c²=3κT/ m₀→а=3κ/ m₀→с=√(3κT/ m₀). R/N_A=k=8,31/6,022*10²³=1,38*10^-23-постоянная Больцмана.

Найдем среднюю кинетическую энергию поступательного движения молекул. Для этого воспользуемся осн. ур-м. МКТ и ур-м состояния для одного моля: PV=2/3 N_А(m₀c² /2)и PV=RT. Учтем, что → PV=2/3 N_Аε, PV=RT. . Для одноатомного газа эта формула выражает среднюю кинет. эн. т.к. отдел атом соверш. только поступательное движение.

Используя соотношение F=-kTlnZ и , необходимо найти PV=RT.В выражении Z мы подразумеваем интегрирование по всему фазовому пространству, т.е. по всем микро состояниям системы. Если такой интеграл подставить и посчитать F, то F окажется неаддитивной, а это противоречит определению термодин. потенциала. Причина в том, что при интегрировании в Z даже в рамках классической статистики, надо учитывать принцип тождественности микрочастиц. Это означает, что микросостояния системы, различ. обменом любых 2х частиц, представляет собой не 2, а одно физическое микросостояние, хотя и соответствует 2м разным точкам фаз. пр-ва. Т.е. при вычислении Z такое состояние нужно учитывать 1 раз. Поэтому интегрирование в Z нужно проводить не по всему фаз. объему, а только по тем фазовым точкам, которые соответ. различным фазовым состояниям.

Если в системе N-тождественных частиц, то каждому микросостоянию соответ. N!- тождественных микросостояний, т.е. N! фазовых точек. →

Расм. идеал. газ в сосуде с объемом V. Внешнее силовое поле отсутствует, но стенки у сосуда присутствуют, представляя барьер ∞ высоты. . Полная энергия идеал. газа .E→Z: Перепишем Z₀, разбив его на произведение интегралов: …

13(2) … Первые 3 интеграла-интегралы Пуассона , а 4-ый → → .Далее Z подставляем в F:→ . Если N-большое число, то имеет место формула Стирлинга: , тогда . Известно, что → →PV=θN. Сравнивая с уравнением Мед-Клап.PV=kTN→PV=RT.

1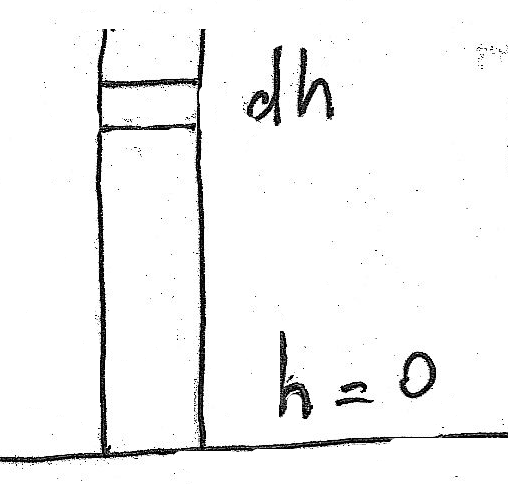 4. Найдём зависимость давления земной атмосферы от высоты. Воздух находится в грав. поле Земли. Хаотическое движение молекул и гравитация взаимосвязаны: при отсутствии тепл. дв. мол-л атмосфера бы лежала на пов-ти Земли, и наоборот, при отс-вии грав-ного прит-ния атм-ра ушла бы в косм. простр-во. Выделим столб воздуха в атмосфере, внутри которого выделим тонкий слой высотой dh. Концентрация и плотность внутри него постоянны. Для изменения давления на данном участке справедлива гидростатическая формула: dp=-ρgdh (1) (знак – в (1) означ., что с ростом h давл. падает), ρ=m₀n (2)-плотн., Воспользуемся ур. Менд-Клаперона: p=nkT, n=p/kT (3), Подставл. (3) и (2) в (1), получ. dp= - (m₀p/kT)gdh или (dp/p)= - (m₀/kT)gdh (4), Будем считать, что Т=const и g=const, тогда интегрируя (4), получим: lnp=- (m₀gh/kT)+c (5). Для определения с восп-ся нач. усл-ми, т.е. будем считать, что на пов-ти Земли (h=0) p=p₀, тогда из (5) получим lnp₀=c (6), Подст. (6) в (5), получим: ln(p/p₀)= -(m₀gh/kT) или p=p₀exp(-m₀gh/kT) (7)– барометрическая формула. Таким образом, с увеличением высоты, давление падает по экспонициальному закону. Здесь T≠T(h). Формула позволяет рассчитывать зависимость давления атмосферы от высоты в случае, если температура атмосферы постоянна, а гравитационное поле – однородно. P=nkT (8), давление на поверхности: p₀=n₀kT (9), Подставляя (8) и (9) в (7) получ. nkT=n₀kTexp(-m₀gh/kT) или n= n₀ exp(-m₀gh/kT) (10) – конц. падает с ростом h.Чем тяжелее газы, тем меньше их на высоте.

Вероятность-численная мера возможности случайного события. W-вер-ть равна отн-ю числа испытаний благоприятвст-х этому данному событию к общему числу испытаний. W=n/N Матеем-ки вер-ть есть limn/N(*) при n→0. Вер-ть измеряется изменяется 0≤W≤1, если W=0, то событие невозможно, W=1-событие достоверно. Рассмотрим случайную вел-ну х. В качестве данной х можно рассм-ть v мал-лы газа, энергию или коор-ты. Плот-ю вероятности f(x) наз-ся вел-на Wf которая будучи умн-я на dx дает вер-ть того что случ. вел-на х нах-ся на отрезке [-x,x+dx]. f(x)dx=dW(x)(1), с др. стороны dW(x)=dn/N(2) нах-ся согл. (*)Обьединяя 1 и 2 получим что плотность вер-ти равна: f(x)dx=dn/Ndx-функция распр-я случ-й вел-ны. Допустим, что вел-на хнах-ся на всей числ-й оси ∫(от -∞ до+∞)f(x)dx=1-усл-е нормировки. Зная f(x) можно выч-ть среднее знач-е данной случ-й велны, как матем-е ожидание. , сред-е квадр-е зн-е . Теорема учня-я вероят-й W(AиB)=W(A)*W(B)

П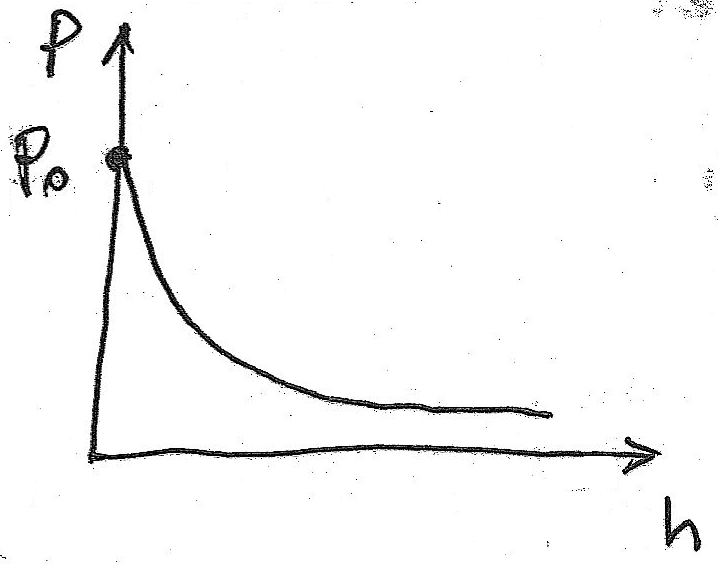 рименим каноническое распределение Гиббса к идеал. газу, наход. в потенц. поле U. , dW(p,q)-вероятность нахождения системы в элементе фаз. объема . E(p,q)-энергия системы, соответ. данному фаз. объему. Перейдем к одной частице. Газ-идеальный, взаимодействие отсутствует.→ . . Проинтегрируем это выражение по координатам и импульсам N-1-й частицы: -вероятность нахождения 1-ой частицы идеального газа с координатами и импульсами лежащими в интервалах:[x,x+dx],[y,y+dy],[z,z+dz],[p_x,p_x+dp_x],[ p_y,p_y+dp_y],[ p_z,p_z+dp_z]. ε-энергия, соответствующая этим интервалам. ε=ε_кин+ε_пот= →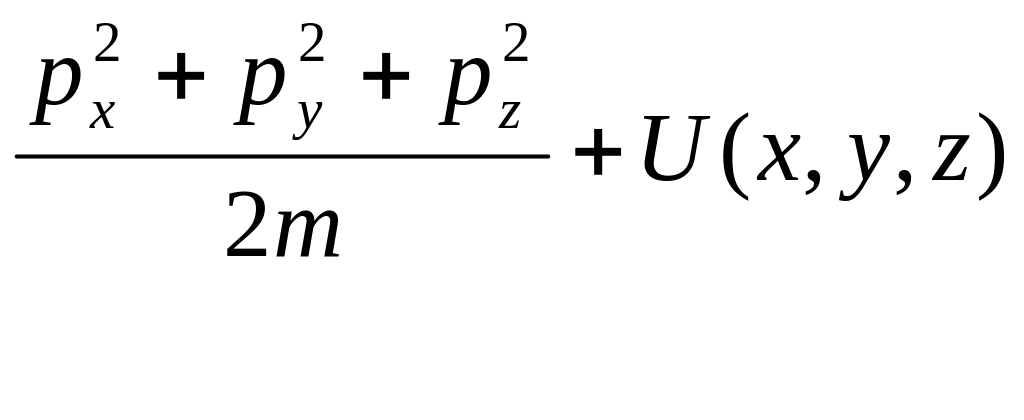

-распределение М-Б.const-определяется из условия нормировки. -распределение Больцмана.

Константу B найдем из условия нормировки: → . Обычно частица нах-ся в поле силы тяж-ти. U=mgz,→

Из условия нормировки: 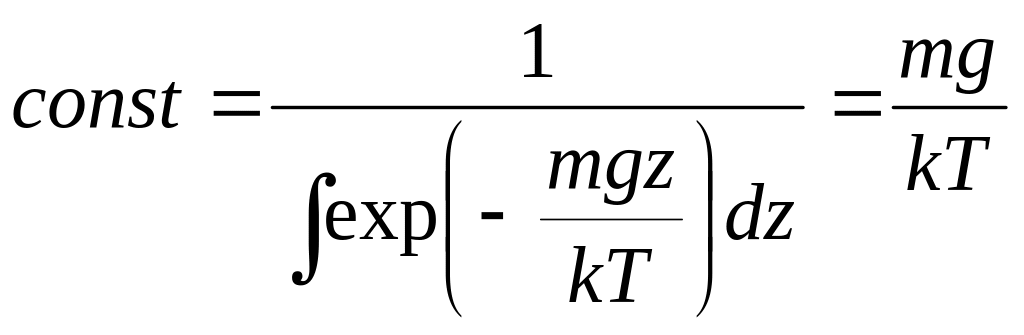, т.о.

Если умножить вероятность на число частиц в 1 объема, т.е. концентрацию:

-в интервале [z,z+dz]. -в интервале [0,dz]. Пусть → , -барометрическая формула.

9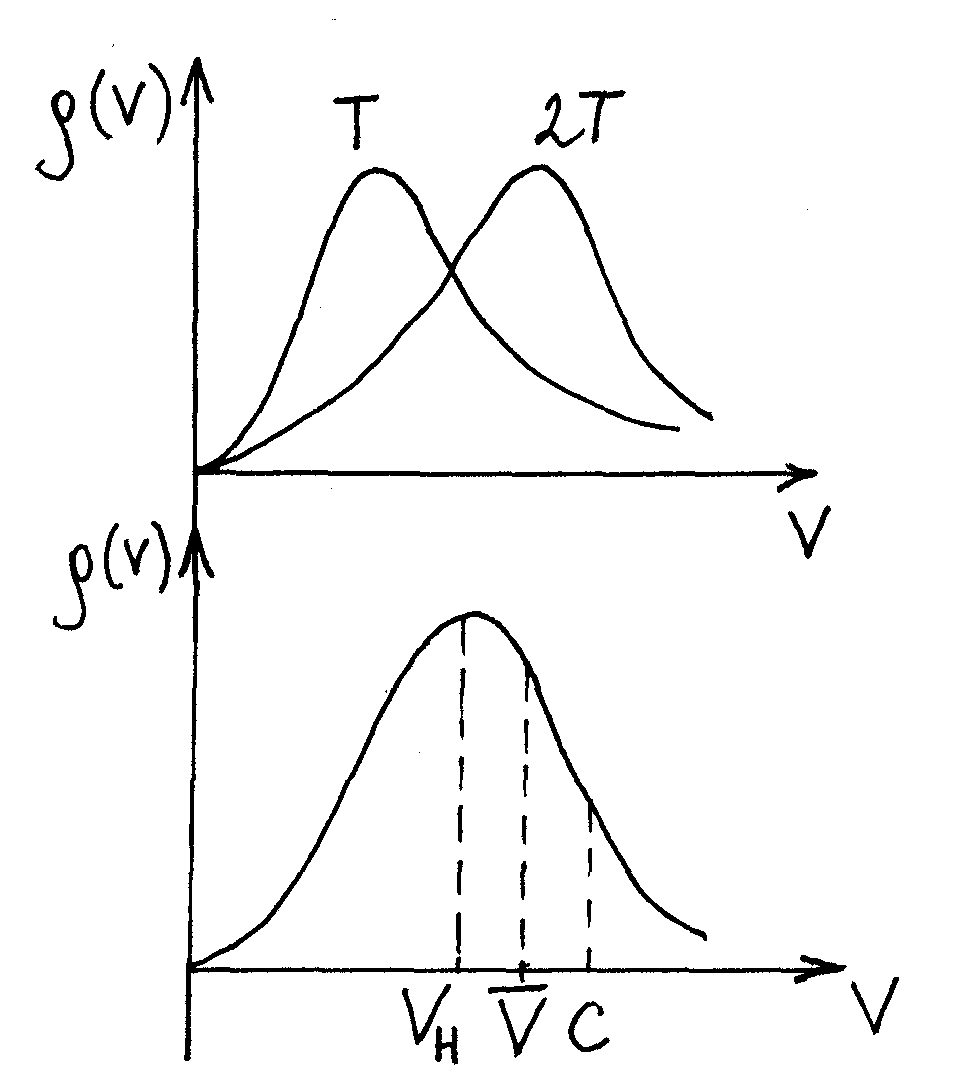 . Рассмотрим однород ид газ с массами молекул m₀ при пост-й температуре. , где α=m₀/2kT, μ(v)dv=dw(v)-вер-ть того, что ч-ца имеет скоростьv. ρ(v)dv=dv/v. Графически это распределение можно представить так:

Физ. смысл: Ф-я распред-я Максвелла определяет вероятность того, что модуль скорости молекулы лежит в интервале (v, v+dv).

Для более высокой температуры кривая распред-я сместится вправо, но несимметрично.

Испол-я распр-е Максвелла по скор-м рассч-ем ср-е арифм-ю и найб-е вероятн-ю ск-ть испол-я функ-ю распр-я массы: ср-е ар-е=матем. ожид-ю ρ(v)=(α/π)^3/2*V²*4π*exp(-αv²) где α=m₀/2kT

-это табл-й инт-л.

1)средн. квадратичн. скорость:

2)Сред-я арифметич. скорость:

3) Наиболее вероятная скорость: -соответствует максимуму ф-ции распределения.

Применим каноническое распределение Гиббса к идеал. газу, наход. в потенц. поле U. , dW(p,q)-вероятность нахождения системы в элементе фаз. объема . E(p,q)-энергия системы, соответ. данному фаз. объему. Перейдем к одной частице. Газ-идеальный, взаимодействие отсутствует.→ . . Проинтегрируем это выражение по координатам и импульсам N-1-й частицы: -вероятность нахождения 1-ой частицы идеального газа с координатами и импульсами лежащими в интервалах:[x,x+dx],[y,y+dy],[z,z+dz],[p_x,p_x+dp_x],[ p_y,p_y+dp_y],[ p_z,p_z+dp_z]. ε-энергия, соответствующая этим интервалам. ε=ε_кин+ε_пот= →

-распределение М-Б.const-определяется из условия нормировки. Умножим это расспр-е на число час-ц: dN(x,y,t,P_x,P_y,P_t,)=N*dW(x,y,t,P_x,P_y,P_t,)- расспр-е по корд-м. -распределение Максвелла.

Перейдем к распределению по скоростям:

т.е. сама ф-я распределения имеет вид:

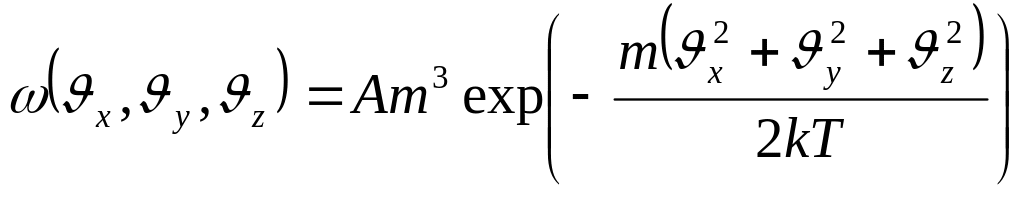
1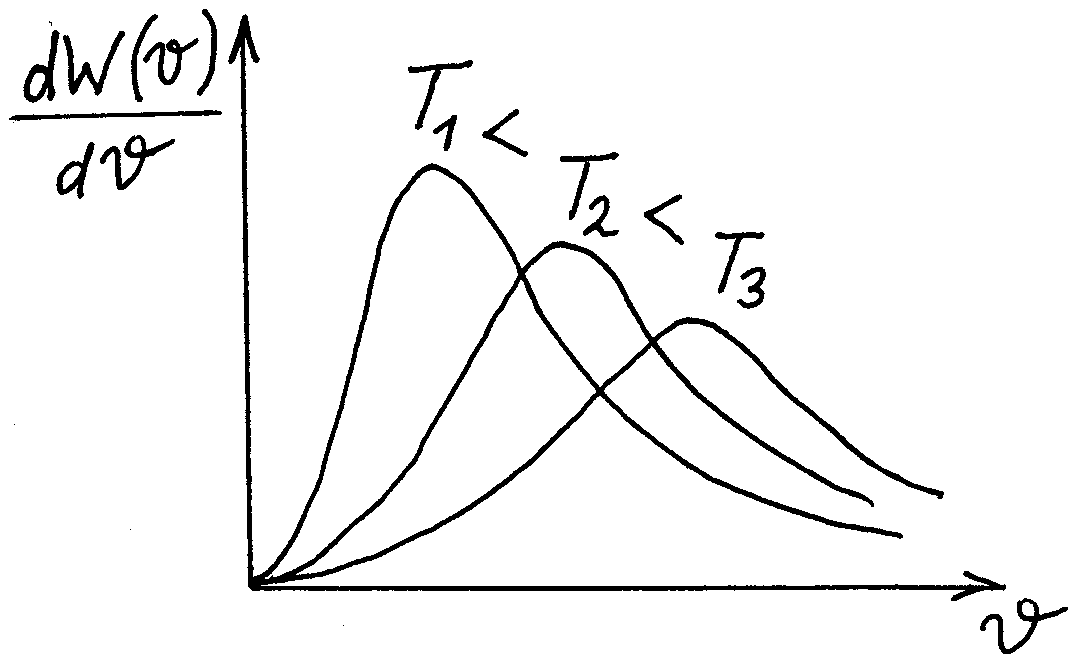 5(2) …Поскольку у молекулы 3-прекции однозначно определяют направление движения и абс. велич. скорости , то ф-я распред. вдоль этого направления должна иметь такой же вид, как вдоль из любой осей: . -плотность вероят, зависящая от абс величины х-ой проекции скорости. Вероят того, что молекула имеет х-ую проекцию скорости в интервале [ ], будет равна: , т.о. . Из условия нормировки:

, получаем: , тогда ,

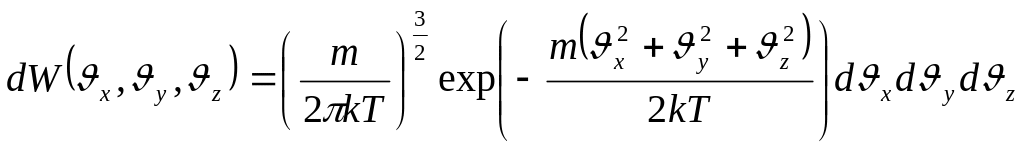-распределение Максвелла по скоростям. Сростом температуры, доля молекул с большим ν увеличивается.

1)средн. квадратичн. скорость:

2)Сред-я арифметич. скорость:

3) Наиболее вероятная скорость: наход из соотношения

10. Внутр. энергия представляет собой сумму энергий, обусловленных перемещением и взаимодействием частиц, входящих в данную систему. В общем случае это сумма кинетич. энергии (обусловлена движ-м атомов и молекул), потенц. (взаимод-е атомов и молекул), энергии химич. взаимод-я (химич. связи), энергии взаимод-я нуклонов внутри ядра. Для ид. газа вн. эн. равна сумме кинетич. энергий отдельных атомов. Если известна средняя кинетич. энергия поступат-го движ-я <ε> одного атома или молекулы, то внутр. энергия сис-мы равна U=<ε>N.Тогда восп-ся основным ур-ем МКТ: pV=(2/3)U (1). В правой части (1) имеем внутр. энергию одноатомного ид. Газа(U=i/2*m/μ*RT), т.к. она включает в себя энергию поступат. движения (молекулы двух и более-атомных газов имеют дополнит. степени свободы), поэтому (1) справедлива только для одноат. газа. Из (1) имеем: U=(3/2)pV (2). Найдем изменение внутр. эн. для произвольного поцесса. Выберем на (p,V) – диаграмме два состояния. (Рис:1) Система произвол-м образом переходит из сост. 1 в 2. Используя ф-цию (2) найдём U для двух сост-ний: U₁=(3/2)p₁V₁, U₂=(3/2)p₂V₂, Тогда ΔU=U₂-U₁=3/2·( p₂V₂- p₁V₁) (3). Как видно из (3), изменение внутр. энергии не зависит от вида процесса p(V), а зависит только от координат нач. и конечного состояния. По этой причине вн. эн. наз. ф-ей состояния. Рассмотрим две взаимод-их термодин-х системы. Различают 2 вида взаимод-я: тепловое и адиабатическое.  взаимод-е сопровождается обменом энергией м/у взаимод-ми телами. Тепл. наз. взаимод-е, при ко-ом взаимод-щие системы не изменяют своих внеш. параметров (напр. объем), то есть передача энергии происходит за счёт теплообмена. Энергия, передаваемая от одной системы к другой при теплообмене, называется колич. теплоты. Взаимод-вие, при ко-ом полностью исключён теплообмен, наз. адиабатич. При этом изменяются внешн. параметры системы. Энергия, передаваемая от одной системы к другой при адиабатич. взаимод-и наз. работой (А). Вычислим элементарн. работу при расширении ид. газа δА=Fdx (6). Рассм. газ внутри цилиндра, ко-ый перемещает поршень вдоль ОХ на dx. (Рис:2) Сила, действующая со стороны газа на поршень равна: F=pS (7). Подст. (7) в (6): δА=pSdx=pdV (8) - применима для всех изопроцессов. δА- неполный дифференциал. Используя (8) можно выч-ть полную работу для произвол-го процесса (Рис.3): A=∫_(1,2) δА=∫_{(V1, V2)}pdV (9). Величина работы численно равна заштрихованной площади из рис.3. Отсюда следует, что полная работа зависит от вида процесса, то есть является ф-ей процесса. Опыт Джоуля:Жидкость известной массы находится в калориметре. Лопасти опущенные в жидкость можно приводить во вращение за счет груза массой m.Он измер. темп. До и после опускания груза, при этом обнаружил: Q=cm(t₂-t_1). Обнаружил приращение теплорода внутри жидкости. Т.о., получено противоречие, результаты опытов нельзя объяснить теорией теплорода. Чтобы объяснить, необход ввести понятие энергии, внутр. эн. жидкости, котор. обусл. взаимод. и перемещ. жид-ти. Результ. Джоуля при пом. эн., объясн. просто: потенц энергия тела массой mпереходит в кенетич. эн. лопостикот. в свою очередьмалекулам жидкости. Измен потенц эн равно:∆E_p=mg∆h,с др. стороны эта величина представляет работу:А=mg∆h,т.о. имеем адиабат. Вз. 2х систем:тела и жидкости, которые обьен. энергией А. Первый закон термодинамики: Колич. теплоты, подводимое к системе, идёт на изменение внутр. энергии системы и на работу, к-ую совершает система: Q=ΔU+A. Запишем 1 з-н термодин. в дифференц. форме: δQ=dU+δА (10); dU=c_vdT (11), где c_v- теплоемкость при v=const. Подставл. (11) и (8) в (10), получ.: δQ=c_vdT+pdV (12). Применение к изопроцессам: 1) Изобарич. процесс (p=const, Q=ΔU+A): Вычислим кол-во теплоты подведенное к с-ме, для этого проинтегрируем (12), получ. (Рис:4) (13). Q=c_v(T₂-T₁)+p(V₂-V₁) (13). A= p(V₂-V₁) – работа, кот. совершает газ против внешн. сил при изобарич. процессе; как видно из рис:4 она выражает площадь прямоугольн. Распишем (13): Q= c_vT₂-c_vT₁+pV₂-pV₁ (14), т.к. U=c_vT; то (14) перепиш-ся: Q= U₂+pV₂ – (U₁+pV₁)=H₂-H₁ (15),где H=U+pV (16). Как видно из (16) всё тепло, подводимое при изобарич. процессе, равно изменению ф-ии Н-энтальпия (ф-я состояния: изменение энтальпии числен= кол.теплоты подведен к сист. изобарически). Данное кол-во теплоты можно расчит. зная c_р: δQ=c_pdT. Тогда интегрируя данное выражение, получ.: Q= c_р(T₂-T₁) (17). Ф-лы (15) и (17) эквивалентны. 2) Изохорич. процесс (v=const, тогда dV=0): в этом случае (12) перепиш-ся: δQ=c_vdT (18). Из (18) следует, что всё подводимое тепло идёт на увеличение внутр. энергии. Интегрируя (18)…

п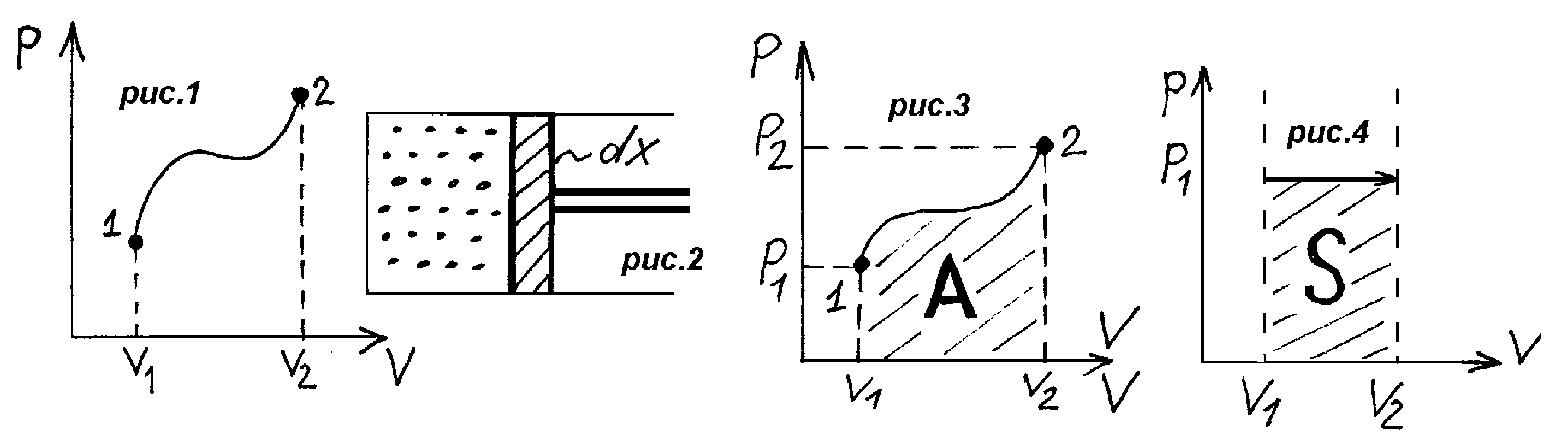 олуч. Q=c_v(T₂-T₁). При изохор. процессе А=0. 3) Изотермич. процесс (Т=const, тогда dT=0): в этом случае (12) перепиш-ся: δQ=pdV= p(V₂-V₁)= δА (19), интегрируя (19), получ.: Q=A – з-н сохр. эн для изотерм. процесса. При изотермич. расширении вся подводимая теплота идёт только на совершение работы. 4) Адиабатич. процесс (процесс, протекающий без теплообмена с окр. средой, т.е. Q=0): тогда (12) переп-ся: c_vdT+pdV=0. Если система совершает работу: δА= - c_vdT, то внутр. энергия уменьшается и газ охлаждается (исп-ся для получения низких температур). Если над системой совершается работа: δА=c_vdT – внутр. энергия увелич., газ нагревается (исп-ся в двигателях внутр. сгорания).

Стат. интеграл им. вид: z=1/N!·(2m₀πkT/h²)^3N/2·V^N (4) Внутр. эн. одноат. ид. газа расчит-ся по ф-ле: U=kT²(δ/δT)(lnz) (5). Подст. (4) в (5), получ: U=kT²(δ/δT){3N/2·ln(2m₀πkT/h²)+NlnV-lnN!}=kT²(3N/2)·(2m₀πk/h²)·(h²/2m₀πkT)=3/2·NkT.

11. Мех-мы преобразующ. теплоту в работу наз. тепл. машинами. Основные узлы: нагреватель – раб. тело – холодильник. Нагреватель, т.к. согласно 1 з-ну ТД работу можно совершать только за счет опред энергии, следов. должен быть источник. раб.тело, т.к. работа-это энергия, кот. передается от 1 сист. к др.адиабатически, следов. нужно тело, кот. будет осущ. этот процесс. Холодильник, тепл. маш. должна работать по замкн. циклу, т.е. переодически. Пусть вначале раб тело расшир при Т-const, соверш работу А, для циклич работы можно вернуть сост.1 при более низкой темпер, или при более высокой. Сам по себе газ сжим. не может следов. нужна внешн. сила. Из рис(3 изотермы в осях PV) видно, что работа при большей Т существенно больше следов целесообразно возвращ сист в исх сост при меньшей темпер. Допустим, что за один акт работы тело получило Q1 и отдало холодильнику Q2 тогда A_n=Q1-Q2,η=A_n *100%/Aз=(1-Q2/Q1)*100%. Любая тепловая машина работает по замкнутому циклу, рабочее тело возвращается в исходное состояние, технически важно возвращать при более низкой температуре. При изотермическом сжатии энергия отдается в окружающ. среду – работает холодильник. Цикл Карно: две изотермы + две адиабаты:1-2 изотермич расширение при Т1, 2-3 адиабатич. расширение, 3-4 изотермич сжатие, 4-1 адиабатич сжатие. Диаграмма в осях T-S(энтропия): переход из S₁ в S₂ при Т₁ имеем Q₁=T₁(S₂-S₁); из S₂ в S₁ при Т₂ Q₂=T₂(S₂-S₁); η=(Q₁-Q₂)/Q₁=1-T₂/T₁. Теоремы Карно: Теорема1. КПД машины Карно не зависит от природы рабочего тела, а зависит от температуры нагревателя и холодильника. Цикл Карно обратим. Теорема 2. Из всех тепловых машин работающих между данным нагревателем и холодильником наибольшим η обладает машина Карно. Холодильные машины: механизмы, которые забирают теплоту у холодных тел и отдают нагретым, т.е. машины работающие по циклу обратному тепловому. Обратный цикл Карно(поменять направлен. стрелок): 1-2 адиабат расширен, 2-3 изотерм расширен, 3-4 адиабатич сжатие, 4-1 изотермич сжатие. Работа внешних сил больше работы, к-ую соверш машина. Для хар-ки эффективности вводится холодильный коэфициет λ=Q₂/A, А-р абота внешних сил рассчитыв. как А= Pt В окружающую среду выделяется энергия Q₁=Pt+Q₂ ,где Q₂ теплота кот. получают от охлаждаемых веществ, Р – мощность компрессора, t – время работы компрессора. В цикле Карно раб-е тело-идеальный газ.

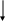
Обратн цикл Карно

К рис11)Q₁=A₁ 2)T₁→T₂ 3)A₂=Q₂эн-я в окр-ю среду4)работа внеш-х сил во внутр-ю эн-ю T₂→T₁

Путь сумма площадей dAa+aBb=q₁, а сумма площадей 2х др= q₂. Для цикла Корно: , где -площадь FABE, -площадь FDCE. Для внутреннего цикла →

12. Процесс при прохождении ко-го в прямом и обратном направлении термодин. система возвращается в исход. состояние не производя изменений в окруж. среде наз обратимым. (матем. маятник). Обратимый процесс явл. последовательностью равновесных состояний, т.е. любой обратимый процесс явл равновесным. Процесс наз. необратимым, если при совершении его в прямом и обратном направлениях система не возвр. в исходное состояние. При этом в окруж. среде происходят изменения (матем. маятник в среде с сопротивлением). Необратимый процесс явл. последовательностью неравновесных состояний, т.е. любой необратимый процесс явл неравновесным. 2-й з-н термодинамики: 1) (Клаузиус): теплота не может сама по себе переходить от менее нагретых тел к более нагретым телам. 2) (Планк): Невозможен такой периодический процесс единственным результатом кот. было бы превращение теплоты в работу (отрицает существование тепловых машин с η=1). 3) (Томсон): невозможно совершить работу за счет охлаждения самых холодных из окруж. тел. 4) (народный): " реальный самопроизвольный процесс явл. необратимым. Введем понятие приведенной теплоты. (Q₁-Q₂)/Q₁=(Т₁-Т₂)/Т₁, Q₁/T₁=Q₂/T₂. Отношение кол-ва теплоты получен. от нагреват. к температуре нагревателя наз. приведенной теплотой, аналогично для холодильника. Приведенная теплота сохраняется. Рассмотрим произвольный замкнутый процесс (обратимый), разобьем весь цикл на достаточно большое число циклов Карно. (рис)

Д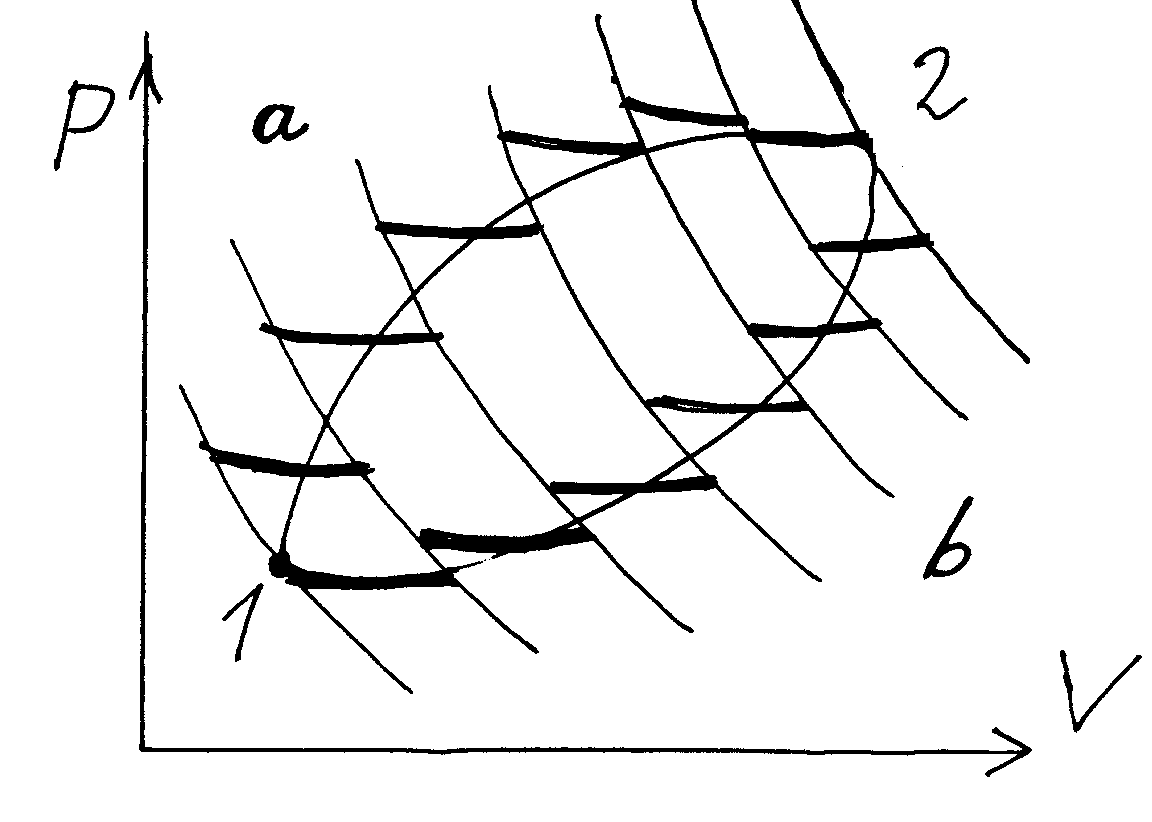 ля i-го цикла можем записать: δQ_ai/T_ai=δQ_bi/T_bi. Просуммируем по N-общее число циклов Корно, известно, что теплота выделенная в окр. среду при изотерм. сжатии отрицательная, т.е. δQ_b<0. Проинтегрируем ∫_1a-2(δQ_ai/T_ai)= ∫_1-2b(δQ_bi/T_bi) и получим, что величина интеграла не зависит от способа интегрирования, а зависит только от конечного и начального состояний, т.е. не зависит от вида процесса. Т.е. данный интеграл равен изменению какой-то функции состояния S. S2-S1=∫(1;2)δQ/T, отсюда dS= δQ/T, для адиабат. Q=0 след S=const (для равновесной замкнутой сист.) Получили неравенство Клаузиуса: S2-S1=∫(1;2)δQ/T=dS для обратимых процессов, а для необратимых S2-S1=∫(1;2)δQ/T≤dS. Принцип возрастания энтропии: если в какой-то момент времени, замкнутая система находится в неравновесном состоянии, то в последующий момент времени наиболее вероятным является возрастание энтропии. Физ. смысл: энтропия замкнутой системы является мерой близости данной системы к равновесию. Тепловая смерть Вселенной: Энтропия мира постоянна, Энтропия мира стремиться к максимуму, т.е. к равновесию. Состояние равновесия вселенной и называется тепловой смертью. Если всел. рассмат. как замкнутую систему, то с течением времени р и Т выровняются и наступит тепловая смерть.

ТДвероятность– число микросост. посредством к-ых реализ. данное макросост(1≤W_T<∞). S=k•lnW_T, т.о. энтропия явл. логарифмической мерой числа возможных микросост. системы. Принцип возрастания энтропии: Воспользуемся первым з-м термодин., когда системе сообщают кол-во теплоты и совершают работу: δQ+δA=dU (2). Рассм. квазистатический процесс, воспольз. канонич. распределением Гиббса. wi=exp(-εi/θ)Ω(εi)/Σexp(-εi/θ)Ω(εi), Z=Σexp(-εi/θ)Ω(εi), dZ=(-1/θ)*Σexp(-εi/θ)Ω(εi)dεi+d(-1/θ)*Σexp(-εi/θ)Ω(εi), можно получить θdZ/Z=-δA+dθ*U/θ, выражаем δA и подставляем в (2) δQ=dU-dθ*U/θ+θdZ/Z=θd(U/θ+lnZ). Величину под знаком дифференциала обозначим через σ, получим δQ=θdσ. Если система замкнута, т.е. энергия и число частиц не меняется, то Q=0 , получим, что dσ≥0 – если в какой-либо момент времени замкнутая система находиться в неравновесном состоянии, то в последующий момент времени, наиболее вероятным является возрастание энтропии .

19. Фазой - наз. физически однородная часть в-ва, которая отделена от остальной части сис-мы границами раздела. Для введения понятия хим. потенциала введём понятия: Термодинамическим потенциалом (т/п) – называются величины, изменение которых определяется только начальным и конечным состоянием тер-кой системы. Т/п Гиббса z =z (p,T) можно ввести через свободную энергию F, знаем, что dF=-pdv–SdT; d(pv)=vdp+pdv; dF=vdp–d(pv)–SdT; d(F+pv)=vdp–SdT; получаем ф-ю состояния z=F+pv; или z=z(p,T), т.к. переменные p и T не являются аддитивными величинами, то т/п Гиббса удобен для практических расчётов. Расм. сис-му число частиц которой не явл-ся постоянным, dz=vdp-SdT+dN, где  - коэф-т, а N - число частиц, а величина dN характеризует скорость изменения числа частиц. Найдём =(z/N)_p,T(1), т.к. p и T величины не аддитивные, то z(p,T)=μ₀(p,T)*N(2), подст-м (2) в (1) имеем =z₀(p,T) - наз. хим. потенциалом, физ. см.- численно равен потенциалу Гиббса в расчёте на одну частицу. Условие равновесия 2 фаз. сист.: Найдём экстр. знач. потен. Гиббса, нерав. Клаузиуса dS≥Q/T; TdS≥dU+pdv или dU≤TdS-pdv, (dU)_v,S≤0, т.е. при постоянных v и S внутр. энерг. уменш. в случ. нер-го процесса и в случ. равновесия U=Umin, dz≤vdp-SdT, (dz)_p,T≤0 или z=z_min, при изобарно-изотермическом процессе, когда система идёт к равновесию потенциал уменьшается и достигает своего min значения, когда dz=0(3) - это условие фазового равновесия наиболее сложных систем. Раскроем (3) воспользовавшись пот. Гиббса, для двух систем, которые обмениваются частицами dz=vdp-SdT+₁dN₁+₂dN₂, где ₁, ₂ - хим. пот. 1 и2 фаз. Чтобы система находилась в равновесии надо чтобы p и T=const, dz=₁dN₁+₂dN₂=0, откуда z=z_min т.к. dN₁=-dN₂ - это усл. равнов. Фаз - число молекул отрывающихся = числу молекул конденсирующихся N=N₁+N₂=const, тогда ₁(p,T)=₂(p,T) - состояние равновесия 2 фаз. сист. - это равенство хим. пот. Различаются фазовые переходы 1-го и 2-го рода. Фазовым переходом 1-го рода наз. такой переход, при котором скачкообразно изменяются первые производные потенциала Гиббса (v,S). Пример: испарение-конденсация, возгонка-сублимация. Фазовым переходом 2-го рода наз. такой переход, при котором скачкообразно изменяются вторые производные потенциала Гиббса =(1/v₀)*(v/p)_T=(1/v₀)*(²z/p²)_T - сжимаемость, Cp=-T*(²z/T²)_p - теплоёмкость. Пример: сверхпроводник - проводник, ферромагнетик - парамагнетик, вязкий гелий - сверхтекучий гелий. Условие равновесия фаз - это равенство хим. пот. Можно получить конкретные значения давления и температуры при которых данные фазы будут находиться в состоянии равновесия. Условие равновесия в диф. форме d₁(p,T)=d₂(p,T), используем хим. пот. на единицу массы, удельную энтропию s=S/m и удельный объём =v/m=1/, ₁dp-s₁dT=₂dp-s₂dT или dp/dT=(s₂-s₁)/(₂-₁) - уравнение Клайперона-Клаузиуса, dp/dT=(T*(s₂-s₁))/(T*(₂-₁)), т.к. TdS=Q, то обозначив T*(S₂-S₁)=q,. т.к. для фазовых переходов 1-го рода является теплота перехода, получим dp/dT=q/(T*(₂-₁)), решим это уравнение для частного случая: жидкость-пар. Учитывая, что пара>жидкости, p*(v/m)=R*(T/), =(RT)/(p), dp/dT=q/T2*(p/R), dp/p=(q/R)*(dT/T2), ln(p)=-(q/R)*(1/T)+C, начальные условия C=ln(p₀)+(q/R)*(1/T₀), p=p₀*exp[(-q/R)*((1/T)-(1/T₀))]-зависимость давления пара от температуры..

О А – кривая сублимации, АВ – кривая плавления, АC – кривая испарения.Три фазы одного вещества находятся в равновесии только в одной точке диаграммы – тройной точке. Для воды - +0,01С; 4,62 мм.рт.ст.

Перегретая жидкость - жидкость, имеющая температуру выше температуры кипения при данном давлении. Перегретая жидкость может быть получена нагреванием в отсутствие в ней центров кипения. Такое состояние жидкости неустойчиво.(Пуз. Камера)

Пересыщенный пар - пар, давление которого превышает давление насыщенного пара при данной температуре, может быть получен при медленном изотермическом сжатии пара в отсутствие центров конденсации. (диз. двиг, камера Вильсона )

20. Запишем выражения квантовой и классической статистик: f_БЭ()=1/exp[((-)/(kT))-1] (1); f_ФД()=1/exp[((-)/(kT))+1] (2); f_МБ()=exp[(-)/(kT)] (3); fкв.()=1/exp[((-)/(kT))±1] (4). Имеем, что ф-я распределения (4) исп-ся искл. для кв-х сис-м, ф-ция распред. (3) исключ. для классич. сис-м. Заметим, что один и тот же газ, напр. электр. газ при опред. усл. подчин. кв. стат. и при опред. усл. может подчиняться классич. стат. Откуда след., что кв. стат. должна переход. в классич. и наоборот. Найд. данные усл. С мат. т. зр. нам необх. найти условия, при кот. ф-я распре. (4) перейдёт в ф. распр.(3). Услов. перехода кв. стат. в классич.: exp[(-)/(kT)]>>1 - классич. распр. exp[(-)/(kT)]<<1(5) - кв. распр. Газ наз. вырожденным, если он подчин. кв. стат. (5) - усл. выр. газа (сильн. выражд.). Услов. (5) долж. выполн. для всех знач. энерг. в том числе и для =0, тогда услов выр. газа: exp[/(kT)]<<1 (7). С целью детальной конкретизации усл. (7) вычисл. концентр. рассм. газа. Для этого рассм. газ, полн. число мол-л кот. N, m₀, v, T. dn=f()d (8). Коль скоро мы находим усл. вырож., то в кач. f() м-но исп-ть в пр-пе любое из 3-х вышеуказанных распред. Коль скоро при дан. усл. вышеуказ. стат. стыкуются между собой, то из сообр. удобства восп. распред. М. Б. dn={(exp[(-)/(kT)])/h³}*d (9). N={(exp[(-)/(kT)])/h³}*d (10). N=exp[/(kT)]*{(exp[(-)/(kT)])/h³}*dvd³p=exp[/(kT)]*(v/h³)*0exp[(-)/(kT)*4p²dp= =exp[/(kT)]*(4v/h³)*0exp[(-)/(kT)*2m*(2m)^1/2*1/2*d= exp[/(kT)]*(2v/h³)*(2m₀)^3/2* 0exp[(-)/(kT)*^1/2d=[0x^1/2*exp{-x}dx= (1/(2))/(/)^1/2]= exp[/(kT)]*(2v/h³)*(2m₀)^3/2*((kT)/2)*(kT)^1/2 = exp[/(kT)]*v*(2m₀kT/h²)^3/2= N; exp[-/(kT)]=(2m₀kT/h²)^3/2*(1/n) (11) n - концентрация. С учётом критерия вырождения (7) его можно переписать следующим образом, исп. (11), (2m₀kT/h2)^3/2*(1/n)<<1 (12). Т.о. нер-во (12) представл. собой более конкретное усл. вырожд. ид. газа. Найдём данное условие: 1. Низкие тем-ры. 2. Малые массы ч-ц. 3. Большие конц-и. заметим, что переход от кв. стат. к классич. реализ. в том случ., когда вел-на (2m₀kT/h²)^3/2*(1/n)=1. Из этого условия найдём температуру выраждения. 2m₀kT/h²=n^2/3; T=n^2/3h²/(2m₀k) (13) оценим температуру вырождения электронного газа в металлах n=1028м-3, m=9,1*10-31 кг, T₀=104 K. При комнатной температуре электронный газ в металле является сильно вырожденным и подчиняется исключительно статистике Ферми Дирака. Формула Планка. f_Б-Э=1/(exp((-)/kT)-1) т.к спин фотона =1. f - средние число фотонов в квантовом состоянии. Для числа состояний d в элементе dГ, d=dГ/h³. Число фотонов: dn=2f_Б-Э()d, dn=2/(exp((-)/kT)-1)(dГ/h³). =(Z/N)_P,T; =Z₀(P,T) если система нах в равновесии, то т/д потенциал Гиббса принимает мин значение, следовательно =0: dn=(2/(exp(()/kT)-1))(dГ/h³). dn=(2/exp(/kT)-1)(dvd³p/h³); du=hdn; du=(2h/exp(/kT)-1)(dvd³p/h³); для единичного объема : du₀=(интеграл по v(du)/v)=2h/(exp(/kT)-1)(1/h³)d³p, du₀=2h/(exp(/kT)-1)(4p²dp/h³)=(2h/h³)(1/(exp(/kT)-1))(4(h/c)²d(h/c)/1)=(8h³/c³)(1/exp(/kT)-1))d; du₀=(,T)d; (,T)=(8h³/c³)(1/exp(/kT)-1)); =h; (,T) - спектральная плотность излучения.

Э лектр-й газ при низкой темп-ре в металле нах-ся в потенц-й яме с линейн-ми размерами ямы, каждый уровень двукратно вырожден, на каждом эн-м уровне есть 2 сост-я разлож-я спина. По запрету Паули на каждом уровне не более 2-х эл-в. Возьмем инт-л [ε,ε+dε]. dn_ср(ε)= n_ср(ε)dΏ, n_ср-число эл-в в данном кв-мсост-и.dΏ-число кв. сост-й. Эл-й газ в металле можно считать идеальным. n-выс-е конц-и, Т-низкие, m₀-малые.

Бозе-конд-я при T₀ <T часть част-ц бозе газа нах-ся на самом нижнем уровне, это явление бозе-конд-и, экспер-но у He при Т=2,19К наблюдаются 2 фазы, одна норм-я, др-я- сверхтекучая, част-цы сидят на нул-м уровне и если их не беспокоить, то они потекут без всякого сопр-я.(Т=10^-9)

14. Электромагнитное взаимодействие-это тип взаимодействия не зависящий от массы частиц и определяющийся фундаментальной характеристикой элементарных частиц зарядов. Существует 2 вида зарядов: положительный и отрицательный. Одноименно заряженные тела-отталкиваются, разноименные-притягиваются.

Св-ва: 1. Заряд любой микро и макро системы кратен е=1,6*10^-19 Кл=4,8*10^-10 CGCE.

2. Во всех процессах происходящих в природе алгебраическая сумма зарядов замкнутой системы не изменяется. Закон сохранения заряда. Строго говоря изменяется алгебраическая сумма зарядов в замкнутой системе. Заряд каждого знака может не сохраняться. Такие процессы имеют место на микроуровне. На макроуровне сохраняется и каждый заряд по отдельности.

3. У всех элементарных частиц имеющих заряд по абсолютной величине один и = элементарному заряду.

4. Заряд любого тела дискретен, т. к. он может меняться лишь на величину кратную е.

Томсон открыл существование во всех веществах одинаковой частицы, обладающей строго определённым отрицательным зарядом. Частицу назвали электрон. Он изучал электрический ток в стеклянных трубках, наполненных газом при низком давлении(катодные лучи). Эти опыты позволили определить e/m для электрона и дали приближенное значение заряда e. Опыты Милликена и Иоффе: в них тела очень малых размеров (капельки масла у Милликена и цинковые пылинки у Иоффе) помещались между заряженными пластинами. Этим крохотным рассматриваемым в микроскоп частичкам можно было специальным образом передать положительный электрический заряд, что приводило к их зависанию. Состояние покоя частичек было вызвано компенсацией противоположно направленных сил тяжести F и электрической силы F_эл. Применяя определённую методику расчёта, можно было измерить заряд частички. В этих опытах был получен очёнь важный результат: частицы могли приобретать только строго определённые заряды, обязательно кратные заряду открытого Томсоном электрона. Частицы с дробным электрическим зарядом не наблюдались, однако в теории элементарных частиц рассматриваются так называемые “кварки”, обладающие электрическим зарядом, кратным е/3. Кварки и лептоны в современной физике выступают как предельная ступень дробления материи. В свободном состоянии кварки не наблюдаются.

Закон сохранения эл. заряд а: Электрический заряд не уничтожается, не появляется. Алгебраическая сумма зарядов остается величиной постоянной-q₁+q₂+q₃+.. q_n=const. Электрические заряды не могут исчезать и появляться из ничего, т. е. суммарный заряд каждого знака в изолированной системе сохраняется. закон сохранения заряда в интегральной форме. Применим к правой части теорему Остроградского-Гаусса: , тогда , можно интегрировать как по объёму занимаемому зарядами, так и по произвольному объёму, поэтому где V-некоторая произвольная область в 3х-мерном пространстве, S-граница этой области, ρ-плотность заряда, -плотность тока ч/з границу.

14. Опыт Кулона: Крутильные весы состояли из подвижного коромысла на одном конце кот-го был подвешен проводящий шарик, а на другом – диск, служащий противовесом. Коромысло подвешено на тонкой серебряной нити, 2-ой шарик находился на неподвижной нити, прикреплённой к крышке весов. В опыте измерялась сила отталкивания между шариками при различных расстояниях между ними. Расстояние позволяла измерять шкала, нанесённая на крышке весов. При зарядке шариков коромысло поворачивалось под действием силы отталкивания, которая измерялась по углу закручивания нити. Каждый заряд возбуждает вокруг себя поле, благодаря которому он в состоянии оказывать силовое воздействие на другие окружающие его заряды, исследуя это явление Кулон установил, закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами в вакууме пропорциональна величине этих зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль линии соединяющей эти заряды. ; -сила, дейст на заряд q₁ со стороны заряда q₂ . Коэффициент κ зависит от выбора единиц. В СГСЭ единица электрического заряда является производной. Она выбирается так, чтобы κ=1. Такая единица заряда называется абсолютной электростатической единицей. Это такой заряд, который действует вакууме на равный ему заряд, удаленный на расстояние 1 см, с силой, равной 1 дине. Тогда: . В СИ единица заряда-кулон. Он является производной и выражается ч/з силу тока и время. Т.к в СИ единица заряда установлена независимо от закона Кулона, то , где ε-электрическая постоянная. Тогда: . Кулоновская сила центральная и направлена вдоль прямой соединяющей эти заряды.

Электрические заряды создают электрическое поле. Осн св-ом явл то, что на находящуюся в этом поле заряженную частицу, действует некоторая сила, т.е. взаимодействие электрических зарядов осущ. по средствам создаваемых ими полей. Поле, создаваемое неподвижными зарядами, не изменяется со временем и наз. электростатическим. Напряженность поля(Е)-векторная величина, равная в каждой точке отношению силы, действующей на единичный положительный пробный заряд(или силовая характеристика поля).Единицы измерения: В/м. Принцип суперпозиции: Напряженность поля, создаваемого несколькими зарядами, равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности.

Следствием закона Кулона и принципа суперпозиции является теорема Гаусса в электростатике: поток вектора напряженности произвольного электростатического поля в вакууме через любую замкнутую поверхность с точностью до множителя π равен алгебраической сумме зарядов, охватываемых данной поверхностью.( ). Для шара: при r>R E=q/R², при r<R -внутри поля нет.

Воспользуемся: (справедлива для любых зарядов:дискретных и непрерывно распределенных). Для записи в диф форме восп-ся теор. Остр-гаусса: , -векторное поле(поток произвольного векторного поля ч\з произв замкн пов-ть S= объемному интегралу от дивергенции). divА характеризует наличие стоков и истоков. Положим => ; -вып-ся для произвольного V. 2 интеграла =при любом одинаковом выборе предела интегрирования.В силу произвольности объема интегрирования а следует теорема Гаусса в диф. форме: . (duv E отлична от нуля, где отлично от 0). Значит лини напряж-ти Эл\ст поля на Эл зарядах если >0-начинаются, <0-заканч-ся. Т о источниками и стоками Эл\ст поля явл-ся заряды.

23 В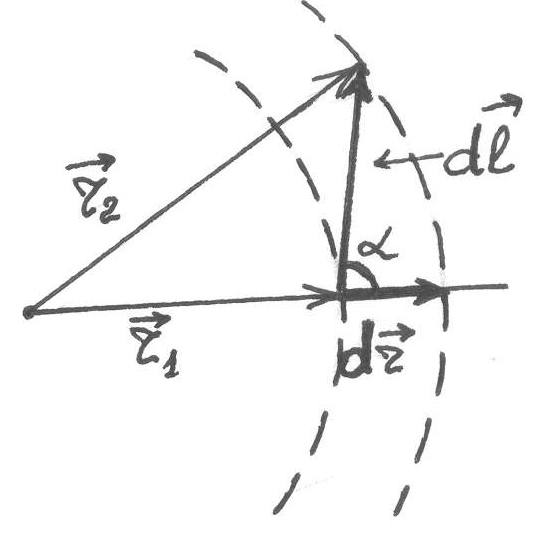 ычислим А по перемещ-ю заряда е^’ в электростат-м поле с (рис). По опред-ю элем-я работа . Чтобы найти А на конечном пути, надо взять интеграл по L. Пусть поле Е созд-ся точечн-м зарядом e, где , т.к , то пол-м , где r₁ и r₂ – радиус-векторы, зад-ие нач-е и конеч-е полож-е перемещ-го заряда е^’ в поле е, т.е. А по перем-ю заряда в электростат поле точечн-го заряда не зав-т от формы пути, а зав-т от нач-го и кон-го полож-я заряда е^’, т.е. это поле потенц-е. Т.к. согл-но принц-пу суперпоз-ии поле любого произв-го заряда м.б. предст-но как суперпозиция полей с-мы точ-х зарядов, то можем утв-ть, что любое электрост-е поле явл-ся потенц-м. Из этого следует, что А по перемещ-ю заряда по замкн-му контуру равна нулю, т.е. циркул-я вектора Е электростат-го поля по замкн-му контуру – интегр-е усл-е потенц-ти электростат-го поля. Введём понятие разности пот-лов м/ду 2-мя т-ми произв-го электростат-го поля – это работа, соверш-я против сил поля по перемещ-ю ед. полож-го заряда м/ду двумя этими точками 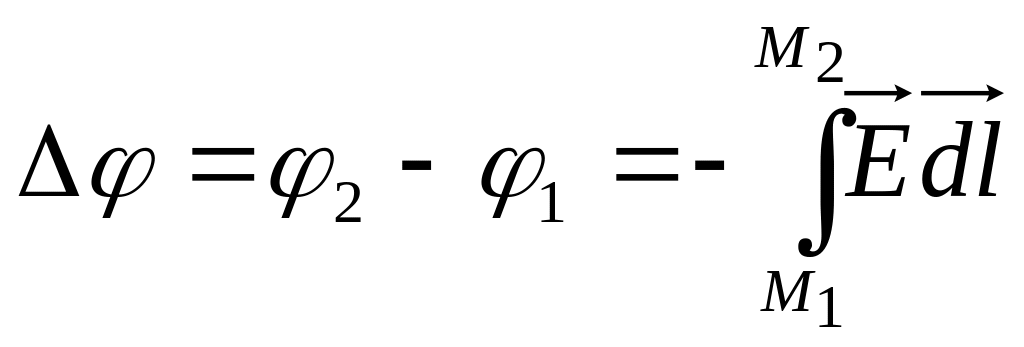. Потенциал любой т-ки поля может быть задан произвольно, разность пот-лов м/ду 2-мя данными т-ми поля опр-ся всегда однозначно. Фиксация потенциала в некоторой точке – нормировка. Обычно нормируют потенциал на ∞, считая что ∞ удал-е точки имеют пот-л 0. При этом потенциал т-ки М численно равен работе, совершаемой против сил поля по перемещению ед. полож-го заряда из ∞ в данную точку . Для колич-й хар-ки электростат-го поля вводят понятие вектора напр-ти - вект-я величина, численно равная силе, действ-й на ед. пол-й точеч-й пробн-й заряд, внес-й в данную точку поля . Принцип супер-ии для электрост-го поля: напр-ть электростат-го поля с-мы неподв-х зарядов равна геом-й сумме полей, созд-х кажд-м зарядом.

Искомая связь: -Е направлен в сторону быстрейшего убывания потенциала, а по величене равен скорости убывания.

Для получения диф условия потенциальности, воспользуемся теоремой Стокса: Циркуляция любого вектора по любому замкнутому контуру равна потоку ротора этого вектора через произвольную поверхность, опирающейся на контур: , тогда: . Из этого ур-я видно: -2-ое основное ур-е электростатики вакуума. Отсутствуют вихри, т.е замкнутых линий напр-ти нет.

16 Проводники –вещества, по кот. могут своб. перемещаться элек заряды. Наличие своб-х электронов в меt явл определяющим фактором, вследствие кот сообщаемый пров-ку из вне заряд распределяется только по поверхности этого пров-ка. Такое распределение сообщаемого пров-ку з-да даёт возм-ть элек полю этого заряда скомпенсировать элек поле, образованное перераспределением по V пров-ка своб-ми электронами. Т.о. поле внутри пров-ка при сообщении ему з-да, отс-ет (Е=0). Т.к. Е= -dφ/dr , при E=0 ,φ=const или 0. Т.о. с др. стороны именно поверхностное распределение сообщ-го проводнику заряда способно удовлетворить усл статичности (неподвижности) его или:  точка на пов-ти или внутри пров-ка им-т φ=const. Во внешнем электрическом поле, в первоначальном незаряженном проводнике начнется движение свободных зарядов. Разделение исчезает при устранение внешнего поля. Заряды, возникшие на поверхности проводника во внешнем электрическом поле, называются индуцированными. А само явление-электростатической индукцией. Оно доказывает существование электрических зарядов в любом проводнике. Заряд на повепхности проводника есть источник , озн что напр-ть поля направлена по нормали. Рассм. прим: пусть -под углом. (рис1).Разложим на нормальное и тангенсиальное. Вдоль возникает сила=>возникает движение, а это уже не электростатика=>должно быть только .При расчете электрического поля полезен метод зеркальных изображений зарядов: если в электрическом поле заменить какую-либо эквипотенциальную поверхность проводником той же формы и создать на нем потенциал, равный потенциалу рассматриваемой эквипотенциальной поверхности, то электрическое поле не изменится.От чего зависит плотность заряда на поверхности проводника? В случае уединенного проводника эта плотность тем больше, чем больше полный заряд q проводника. Если это тело-шар, то заряд q распределен по его поверхности равномерно, поверхностная плотность повсюду одинаковая . Т.к. напряженность эл поля, создаваемого равномерно заряженным шаром вблизи поверхности равна: , подставляя q через σ. получим: , справедливой в общем случае. Выразим σ через φ: . Т.е. при заданном заряде, σ обратно пропорциональна R. Поверхностная плотность заряда будет в тех местах, где меньше R, т.е. где больше кривизна. Роль острия(электрический ветер).Напряженность поля вне проводника вблизи его поверхности: (в СИ , в СГСЭ ).

Уединенный проводник-проводник, на который не действуют поля проводников или заряженных тел(заряды противоположного знака находятся на бесконечности). Электроемкость численно равна заряду, который надо сообщить проводнику, чтобы изменить его потенциал на единицу.( ). Электроемкость определяется геометрической формой и размерами проводника, диэлектрической проницаемостью среды, в которой он находится. Она не зависит от вещества проводника и находящегося на нем заряда.

Расм. электроемкость шара. При сообщении шару заряда q вокруг него возникает электростатическое поле, которое образовал бы точечный заряд. Поэтому потенциал шара относительно бесконечности буде: . С др. стороны: (в СГСЭ ). В СИ единицей электроемкости является 1 Фарад-емкость уединенного проводника, потенциал которого увеличивается на 1 В при сообщении заряда в 1 Кл. В СГСЭ электроемкость имеет размерность длины и измеряется в сантиметрах.

Рис.1

16. Диэлектрик - в-во, не провод-е эл-й ток: полярные и неполярные. Диэлектрик, помещенный во внешнее электрическое поле, поляризуется, т.е. приобретает дипольный момент P_e . Интенсивность поляризации характеризуется вектором поляризации , который определяется как дипольный момент единицы объема. Если диэлектрик поляризован однородно: . Ясно, что дипольный момент, а следовательно вектор поляризации зависят от напряжения внеш. эл. стат. поля: , где α-коэффициент, наз. поляризуемость диэлектрика, и хар-ся спос-ть этого в-ва (диэл-ка) поляризоваться во внеш элек поле. , где χ(каппа)-диэлектрическая восприимчивость. Вектором поляризации наз.-предел отношения суммарного эл-го мом-та какого-либо объёма V в-ва к этому объёму, когда последний 0. ΔP=dp_е^/dV из опред-я в-ра поляриз-ции в-ва  что физич-ки он предст-т собой эл-й момент единицы объёма. Все з-ды нах-ся в связанном сост-ии в атомах или мол-ах и при внесении во внеш элек п м\т перемещ-ся на микрорастояния в пределах атома или мол-л, смещаясь из одного положения равновесия в другое – это явление наз поляризацией диэлектриков. Неполярные - атомы или мол-лы, кот в отсутствии внеш элек п облад-т нулевым элек мом, т.е. при назв-х усл-х, центр тяжести «-» з-да атома (мол-лы) совп-т с центром тяж-ти + з-ов. В электрическом поле оба заряда смещаются в противоположные стороны и при неочень сильных полях, это смещение можно положить пропорциональным напряженности эл. поля. Описанный тип поляризации наз. электронным. Полярный - атомы (мол-лы) кот в отс-вии внеш элек п обл-т ненулевым диполн. мом. Однако в следствии теплового движения в отсутствии поля молекулы расположены хаотически. При наложении внешнего эл. поля, на каждый диполь действуют силы, стремящиеся его ориентировать параллельно полю. При этом сумма дип. моментов не равна 0, диэлектрик приобретает электрический момент. Описанный тип поляризации наз.-ориентационной.

σ^’ –поверхностная плотность связ. зарядов. Пусть диэл-к имеет форму косого параллелепипеда. Поместим его в поле . Объем диэл-ка рассм-м как макродиполь. (P_l дипольный момент). = . = -нормальная составляющая в-ра поляризации, кот численно равна поверхностной плотности связанных зарядов. .Рсм. плоский конденсатор, (рис)заполненый дмэлектриком с ε. Введем в расмотрении вектор электрической индукции: . В присутствии диэл-ка результирующее поле . Е=Е₀-Ед. Е₀-напряженность поля своб-х зарядов.В присутствии диэл-ка поле порождено связ. Зарядами и свободными.Из связи между Е и σ имеем: . => => => ε=1+ .

Р асчитаем напряженность поля внутри и вне шара радиусом R , изготовленного из диэлектрика с ε. несущий заряд q: по теореме Гаусса имеем: ,

.

При r<R

При r>R

17/ Электрический ток-направленное движение заряженных частиц под действием электрического поля.

Постоянный электрический ток-это ток при I=const. Сила тока -заряд в единицу времени.

Плотность тока -сила тока через поперечное сечение проводника. Напряжение

Условия существования эл. тока: наличие носителей заряда, Э.Д.С, замкнутость цепи.

Закон Ома для участка цепи: ток в участке цепи прямо пропорционален падению напряжения на этом участке цепи и обратно пропорционален сопротивлению этого участка. .

Закон Ома для замкнутой неразветвленной цепи: ток в цепи прямо пропорционален Э.Д.С источника и обратно пропорционален полному сопротивлению цепи. . где r-внутреннее сопротивление источника.

Правила Кирхгофа:

1). Алгебраическая сумма токов сходящихся в узле равна нулю. (следствие закона сохранения заряда).

2). В  контуре мысленно выделенного в разветвленной цепи алгебр ∑ падений напр-ий создаваемых соответствующими токами на соответствующих участках выделенного контура = алгебр ∑ ЭДС действующих в этом контуре.( следствие закона сохранения энергии).

Закон Джоля-Ленца в интегральной форме: ω-плотность тепловой мощности. -закон Ома в диф. форме. /

σ-удельная проводимость =1/ρ. . :количество теплоты, которое выделяется в проводнике при прохождении электрического тока I, пропорционально квадрату силы тока I², сопротивлению проводника R и времени.

Механизм выделения Джоулева тепла: при движении электрона в металле под действием электрического поля, происходит их столкновение с узлами кристаллической решетки. При этом происходит искажение кристаллической решетки. На искажениях кристаллической решетки происходит рассеяние энергии движения свободных электронов. Энергии движения переходит в тепловую энергию и выделяется в проводнике в виде теплоты.

Закон Ома в диф. форме: , где е-заряд электрона, n-концентрация, -упорядоченная скорость заряда(дрейфовая), j-плотность тока.

, где -средняя длина пробега, ν-тепловая скорость, a-ускорение.

, где m_е-масса электрона, Е-напряженность эл. поля.

.

-ур-ние непрерывности(з-нсохр. заряда в диф форме); в точках, где , т к , -условие стационарности.

18.Магнитное поле – одна из форм проявления электромагнитного поля. Оно создается проводником с током, движущимися электрически заряженными частицами и телами обладающими магнитным моментом, а также изменяющемся во времени электрическим полем. Для характеристики интенсивности магнитного поля используется индукция магнитного поля . За направление вектора магнитной индукции в данной точке пространства принимается направление силы действующей на северный полюс магнитной стрелки. Силовыми линиями магнитного поля наз-ся кривые касательные в каждой точке к которым совпадают с направлением вектора магнитной индукции в данной точке пространства

З 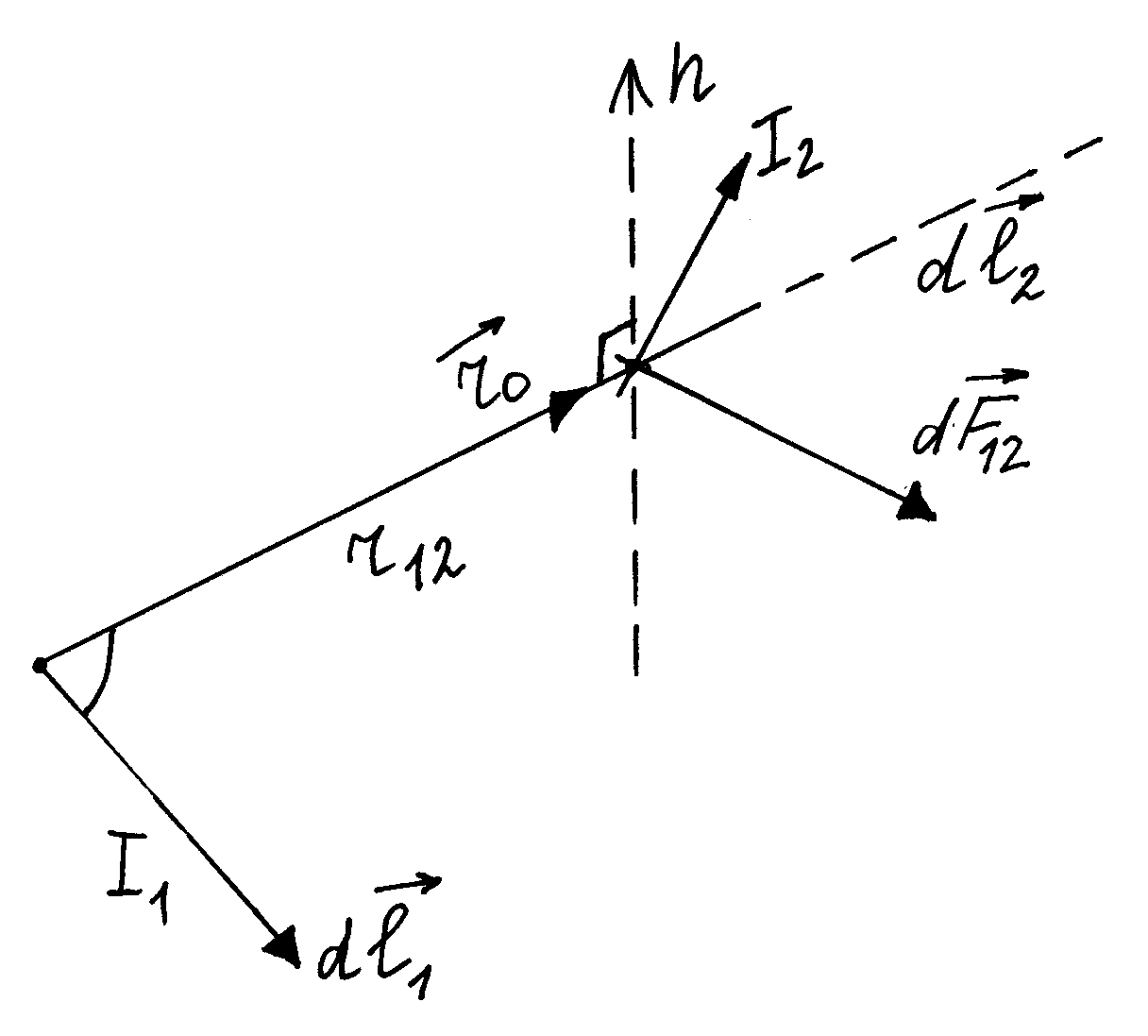-н Ампера:

Экспериментально установил закон о механическом взаимодействии 2ух токов, текущих в малых отрезках проводников, находящихся на расстоянии др. от др.

Если в магнитном поле индукции , поместить проводник длиной  с током I и существует угол между двумя векторами (I^,В^); (^,В^), I^^, поле однородно

В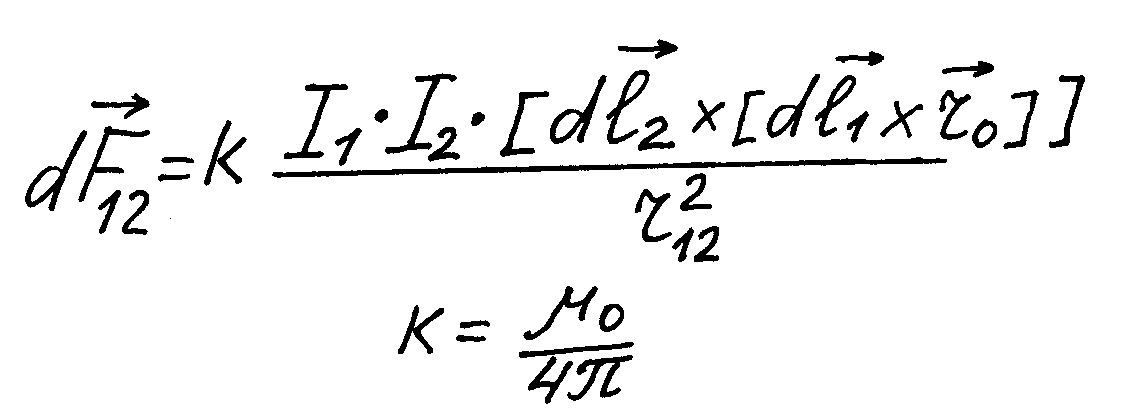 =const, тогда на этот проводник действует сила ; F=IB sin(( )). Если поле не однородно, то надо выбрать такой участок длины d проводника, в пределах которого можно считать В=const , тогда , -выражение для силы Ампера позволяет дать толкование индукции В в каждой точке. ; =1; I=1; sin(^,В^)=1;тогда численно = силе, действующей на проводник единичной длины с единичной силой тока на проводник расположенный перпендикулярно .

Аналитическая форма закона Био-Савара-Лапласа: ; ₀=4*10⁷(Bc/mA), -безразмерная величина, называемая магнитной проницаемостью среды, окружающий проводник длиной d по которому течет ток I.(рис1). .

В ычислим индукцию магн поля бесконечного прямолинейного проводника с током I на расстоянии R от него.(рис2).

В ывод закона полного тока: в электростатическом поле циркуляция вектора, -это свидетельствует о потенциальном характере этого поля. Вычислим циркуляцию вектора Н: …

27(2) … . Возьмем контур l охватывающий проводник с током I. – циркуляция статического магнитного поля не равна нулю что свидетельствует о непотенциальном характере магнитного поля. Такие поля наз-ся вихревые. Полученный результат свидетельствует о том, что в природе отсутствуют магнитные заряды. . Если внутри контура обхода находится несколько проводников с током, то – закон полного тока. Опр.: Циркуляция вектора по замкнутому контуру, охватывающему систему токов, равна алгебраической сумме токов, охватываемых этим контуром, и равна 0, если контур токи не охватывает.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода контура правилом правого винта. Закон полного тока позволяет находить магнитную индукцию без применения закона Био-Савара-Лапласа.

Закон полного тока в диф. форме: применим закон полного тока для бесконечно малой окружности, через которую протекает ток dI: , где dS-площадь контура.

-свидетельствует о не потенциальности магнитного поля.

Система Д.У: или . 1-ое ур-е говорит о замкнутости силовых линий магнитного поля-не существует магнитных зарядов. 2-ое ур-е -не является градиентом никакой функции координат (скалярной). Означает, что магнитное поле не потенциально (вихревое).

20. Явл э\м индукции: переменное м поле создает вихревое эл поле, кот и обус-т воз-ие в пров-ке индукц тока.28. Опыты Фарадея: 1) В момент замыкания и размы-кания ключа-стрелка гальванометра откланяется. Если в 1 ток не изменяется, то гальванометр не реагирует( в 2 тока нет).

2 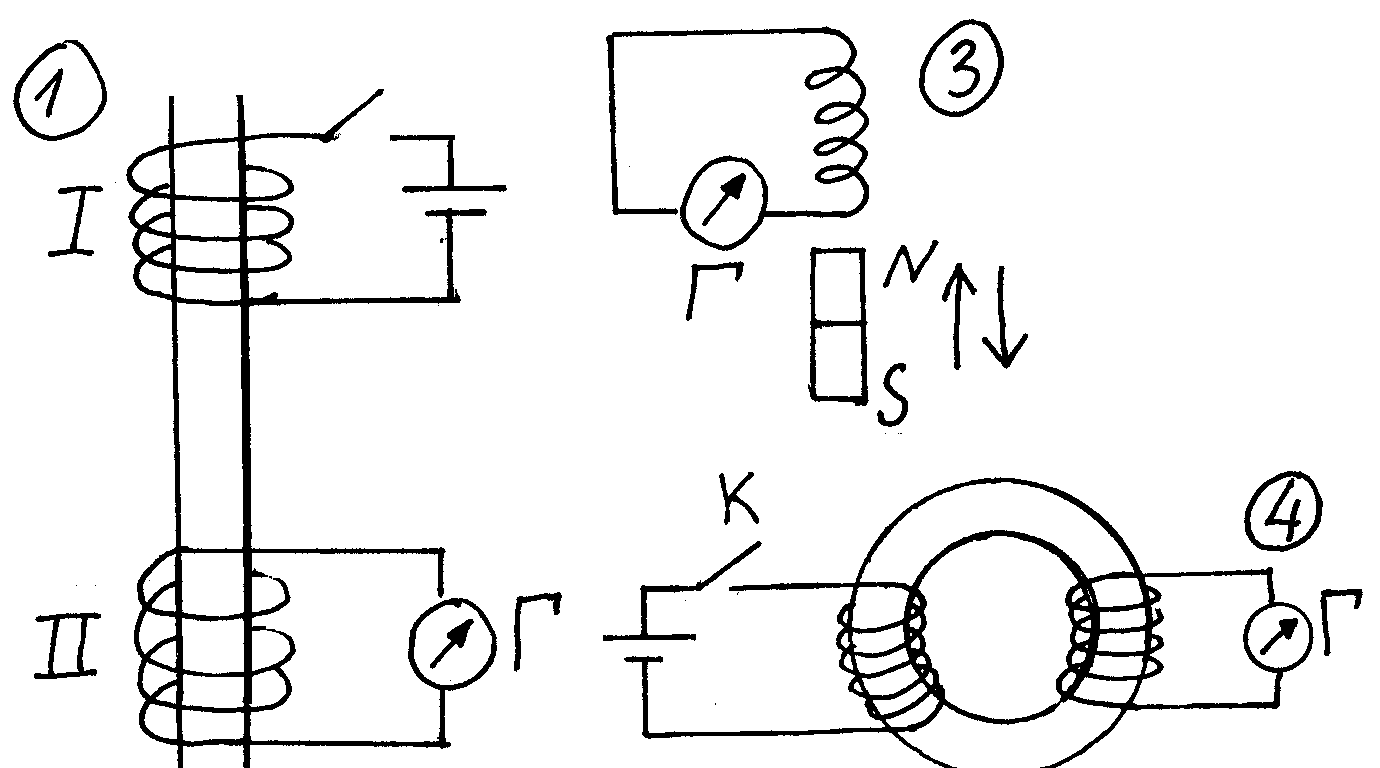) При движении 1 по сердечнику-стрелка гальванометра отклоняется.

3) При введении и выведении магнита из катушки- стрелка гальванометра отклоняется( Изменение магнитного поля-причина отклонения стрелки).

4) Взял 2 тороида: деревянный(I_дер) и железный(I_жел). → I_жел I_дерВ обоих случаях Н одинаковое. Т.о. причина изменения I:

Закон электромагнитной индукции: ЭДС индукции( ) в замкнутом проводящем контуре пропорционально скорости изменения магнитного потока через площадь, ограниченную контуром. , где к=1-коэф. пропорциональности.

П 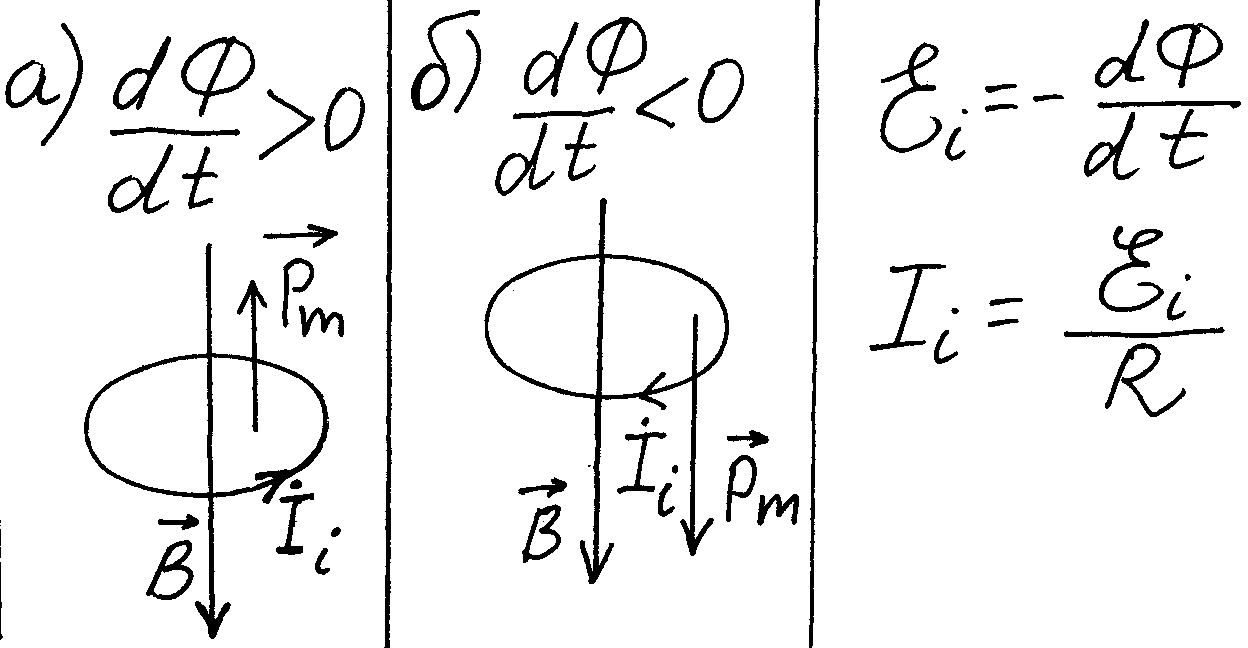равило Ленца: В замкнутом контуре возникает ток индукции I_i такого направления, при котором его собственное магнитное поле препятствует изменению того магнитного поля, которое породило ток индукции I_i.

Механизм возникновения ЭДС индукции:

1). Постоянное магнитное поле: при установившемся движении за счет силы Лоренца на электроны в проводнике, электроны скопятся в 2. Поэтому возникает разность потенциалов: . По закону Ома для неоднородного участка цепи: , I=0(цепь разомкнута), . т.к. никаких источников в l нет, значит → .

2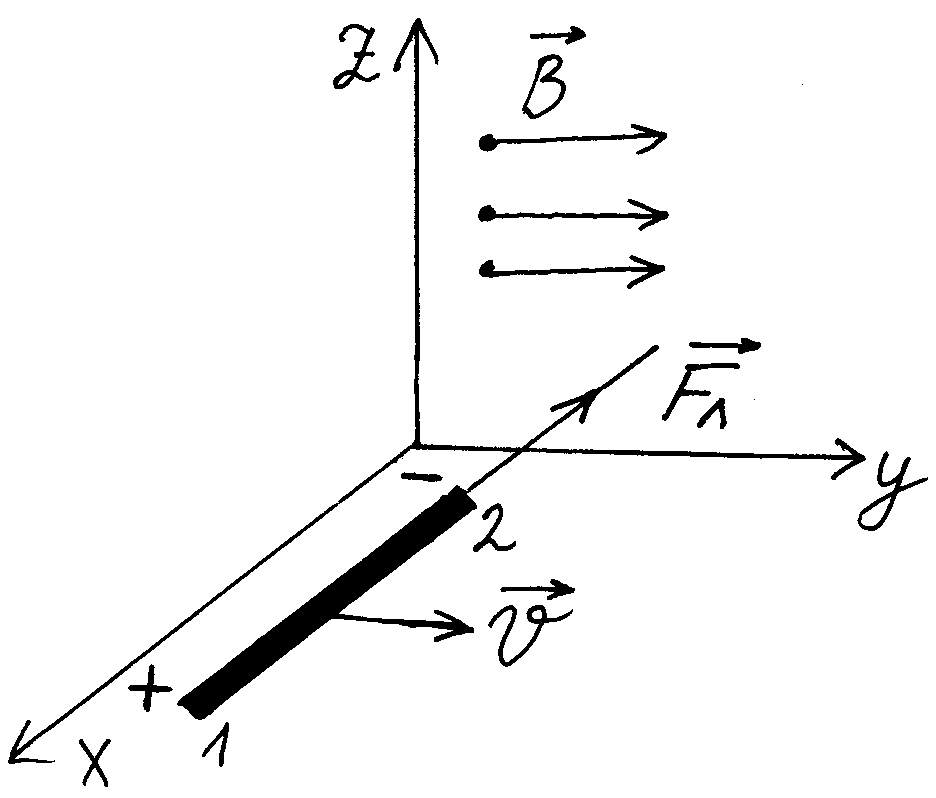 ). В неподвижных проводника постулируется: переменное магнитное поле-причина возникновения в замкнутом проводящем контуре электрического поля . Из принципа суперпозиции: , по определению:

. Второй интеграл=0.→ .

Закон электромагнитной индукции в интегральной форме:

(2)-циркуляция вектора напряженности электрического поля вдоль контура l, определяется скорость изменения потока магнитной индукции через поверхность S, охватываемую джанным контуром . Обобщение состоит в том, что мы выбрасываем проводник как существенное.Перейдем к з-ну э\м инд. в диф форм. Исп-м теорему Стокса (3)сравнивая(2)и(3) получаем => -диф форма з-на э\м индукции. Неразрывная связь между Эл и магн полем. Проводник играет роль индикатора, по возникновении в нем тока м судить: возникло вихревое эл поле.

29 Рассмотрим среду в которой отсутствуют токи проводимости. Однако в такой среде всегда существуют микро-токи, которые реализуются за счет движения электронов по орбитам в пределах атома или молекулы по замкнутой траектории. Такие токи наз - молекулярными. Так как имеет место замкнутый ток, можно приписать ему определенный магнитный момент. В случае отсутствия внешнего магнитного поля, магнитные моменты молекулярных токов ориентированы хаотично и в этом случае суммарный магнитный момент, а следовательно и магнитное поле создаваемое молекулярными токами = 0. Мерой намагничивания магнетика служит вектор интенсивности намагничивания: –наз предел к которому стремится отношение суммарного индуцированного магнитного момента какого-либо объема вещ-ва к этому объему когда последний стремится к нулю: 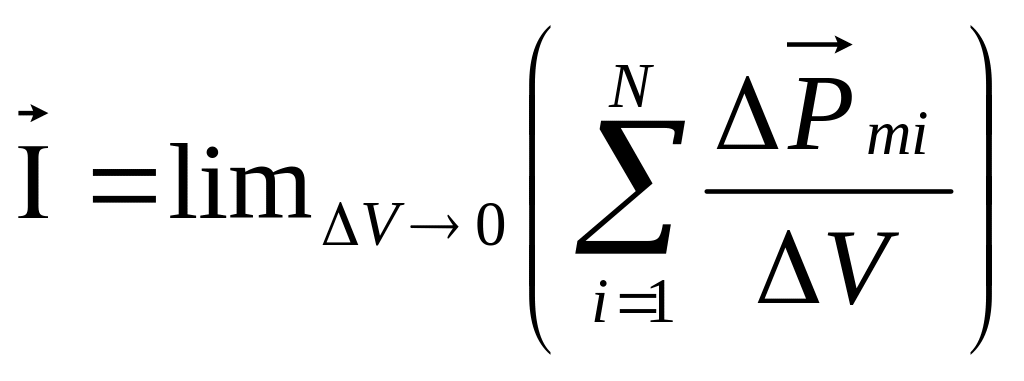,где -магнитный момент i-го атома. _V-рассматриваемый объем вещ-ва. N-число атомов в _V. Если вещ-во однородно, то для каждого атома такого вещ-ва, в _V, будет одинаковым и тогда: -где n₀₌N/_V. Сущ-ет связь между вектором интенсивности намагничивания и в-ром напр-ти магн-го поля: =æ_m ; æ_m – является безразмерной и наз-ся магнитной восприимчивостью вещ-ва. Она характеризует способность этого вещ-ва намагничиваться внешним магнитным полем. Вектор напряженности магнитного поля . , , , где i_m – молекул. ток. Для : (1) – как видно из ф-лы (1) предст-ет собой сумму двух различных по своей природе векторов и след-но не имеет ярко выраженного физического смысла. Если поместить магнетик в магнитное поле, то поле внутри магнетита представляет собой суперпозицию внешнего поля и поля намагниченного магнетита: , Изв-но, что Подставляем : ; . =æ_m+1-магнитная проницаемость. При внесении во внешнее магнитное поле магнитные моменты молекулярных токов ориентируются определенным образом, либо по направлению вектора индукции внешнего магнитного поля, при этом магнитное поле внутри магнетика усиливается (парамагнетик), либо против - поле ослабляется (диамагнетик). В обоих случаях поле внутри по величине не сильно отличается от внешнего. Диамагнетики – вещ-ва магнитный момент атомов (молекул) которых в отсутствие внешнего магн. поля =0 (водород, азот) <1, æ_m<0. Парамагнетики - вещ-ва магнитный момент атомов (молекул) которых в отсутствие внешнего магн. поля 0, причем в отсутствие внешнего магнитного поля эти магн моменты , за счет теплового движения в объеме всего парам-ка дезориентированы, суммарный магн мом всего объема =0 (вода, алюминий) >1, æ_m>0. У ферромагнетиков поле внутри сильно отличается от внешнего и для них характерна остаточная намагниченность в отличие от пара - и диамагнетиков. Особенностью является то, что застройка электронами электронных оболочек не соответствует закону. Если бы в атоме железа соблюдались условия, то 26 его электронов образовали бы 3 оболочки :1 об-2; 2об-8; 3об -16. Однако в атоме железа 4 оболочки : 1об-2, 2об-8, 3об-14, 4об-2. В каждой оболочке электроны разбиты на слои. Таким образом в третьем слое третьей оболочке есть нескомпенсированные 4-спина. В кристаллической структуре образуются группы атомов, спины которых ориентированны одинаково образуя макро области называемые –доменами. Свойства: диамаг. выталкиваются из магнитного поля, а парамаг. втягиваются в о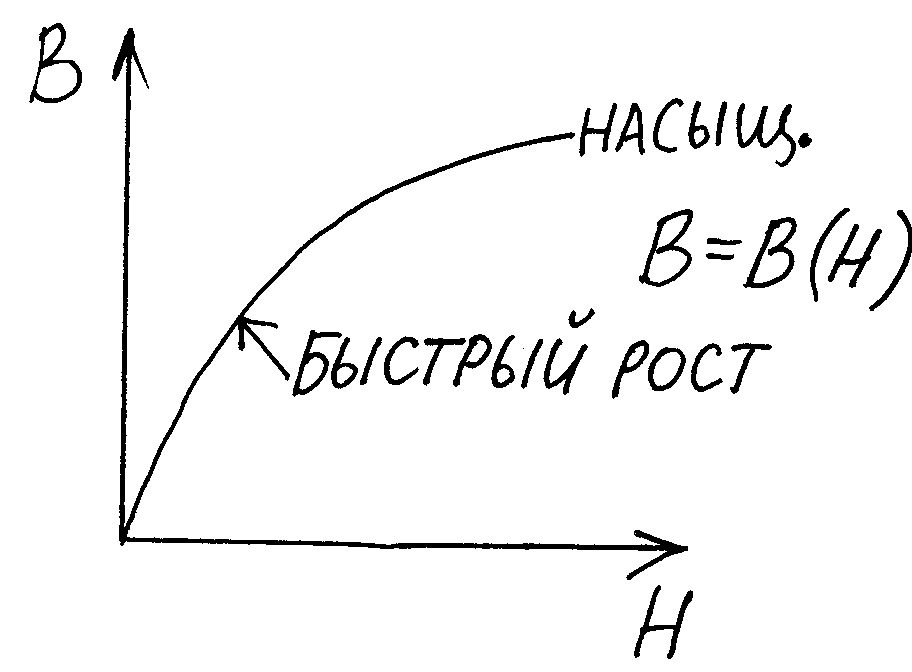 бласть сильного поля. Магнитная проницаемость у феромагн. при обычных температ. измеряется сотнями, тысячами единиц. Есть способность сильно намагничиваться. Характерная особенность – сложная зависимость между индукцией В и напряженностью поля Н.

Кривая намагничивания: зависимость индукции поля внутри ферромагнетика от напряженности внешнего поля.

Г истерезис: значение индукции в феро-ке определяется не только существованием магнитного поля но и зависит от предыдущих состояний намагничивания. Причем происходит отставание изменения индукции от изменений напряженности поля. Это явление наз – магнитным гистерезисом. Ферромагнетики испол-ся в кач-ве эл-тов запомин-щих устройств в ЭВМ и испол-ют в пост-ных магнитах.

21. Перем.ток – это ток амплит и направл кот-го измен-ся со времм. Гарм-ий перем. ток – электр.ток, котор измен-ся с теч времени по гармон закону. Действующее значение перем тока – такое знач тока, при кот этот ток оказывает такое же действие как ток в цепи постоянного тока. i=I_msint, i - мгновенн значение тока., I_m - ампл тока, T=1/ - наименьш промеж времени через кот-ый значение силы (напря- жения) тока повторяется.  - частота ; =2,  - угловая частота. Если цепь, в которой напряжение на реактивных сопротивлениях много меньше напряжения на резисторе, то это – цепь с активным сопротивлением. В цепи с активным сопротивлением происходит необратимое преобразование энергии электрического тока во внутреннюю энергию проводника, т.е. – выделение джоулева тепла. Мгновенная мощность есть произведение мгновенных значений тока и ЭДС: p=ie=I²_mRsin²t. Амплитуда мощности: P_m=I²_mR. Вычислим среднюю мощность переменного тока за период. Надо работу, совершаемую током за это время разделить на период (рис1). Из определения мощности следует, что это элементарная р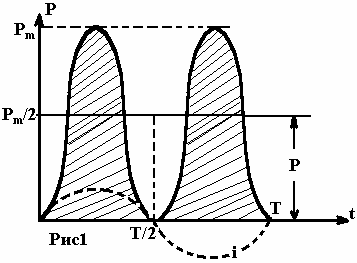 абота ∆A=p∆t; полная работа изображается площадью под графиком. Из свойства синусоиды следует, что площадь, заштрихованная под кривой, равна площади прямоугольника, основание которого равно периоду, а высота - половине амплитуде мощности. Работа за период: A=(1/2)P_mT=(1/2)I²_mRT; средняя мощность: P=A/T=(1/2)P_m=(1/2)I²_mR. (1) Сравнивая это выражение с формулой для вычисления мощности постоянного тока: P=I²R, получим: I²R=(1/2)I²_mR. Отсюда следует : I=I_m/2^1/2. –эта величина называется действующим значением переменного тока. e=e_m/2^1/2 и U=U_m/2^1/2 –действующими значениями ЭДС и напряжения. Если цепь с переменным током содержит только резистор R, к которому приложено переменное синусоидальное напряжение U=U_msint, то ток i в цепи будет определятся значением этого сопротивления i=U/R=(U_m/R)sint=I_msint, где I_m=U_m/R - амплитуда тока, при этом ток i и напряжение U совпадает по фазе. Цепь с катушкой индуктивности L, для которой R=0, U=U_msint. Протекающий через катушку переменный ток i создаст на ее обмотке переменное ЭДС самоиндукции e_L, тогда U+e_L=0, e_L=-L(di/dt); di/dt=-e_L/L=U/L=(U_m/L)sint, проинтегрируем i=-(U_m/L)cost+A=(U_m/L)sin(t-/2)+A, где А - постоянная интегрирования., i=I_msin(t-/2), U/L=I=U/X_L, где X_L-индуктивное сопротивление. I=U/X_L - закон Ома для цепи переменного тока с индуктивностью. Цепи с емкостью: U=U_msint, R=0, X_L=0; i=dq/dt; q=CU; i=d(CU)/dt=CU_msin(t+/2); i=I_msin(t+/2); т.е. ток как и приложенное напряжение, изменяется по закону синуса, но опережает его по фазе на /2, СU=I; U=I(1/C), здесь 1/C - имеет размерность сопротивления и наз-ся – емкостным сопротивлением – X_C=1/C; I=U/X_C -закон Ома для цепи переменного тока с емкостью. Цепь из R, L, C. Условие электрического равновесия: U=U_R+U_L+U_C; здесь ток во всех трех последовательно соединенных сопротивлениях один и тот же: i=I_msin(t). Напряжение на этих сопротивлениях: U_R=iRsint; U_C=I_mX_Csin(t-/2)=-I_mX_Ccos(t); U_L=I_msin(t+/2) =I_mX_Lcos(t). Так как ЭДС: e=U_msin(t+) есть сумма колебаний напряжений, а так как они различны по фазе, то для их сложения удобно воспользоваться векторной диаграммой (рис2). По теореме Пифагора: U_m=(I²_mR²+I²_m(X_L-X_C)²)^1/2. Z=(R²+(X_L-X_C)²)^1/2 = (R²+(L-1/C)²)^1/2 - наз-ся полным сопротивлением цепи переменного тока. Как видно амплитуды колебаний тока и ЭДС связаны соотношением: I_m=U_m/Z – закон Ома для цепи переменного тока.

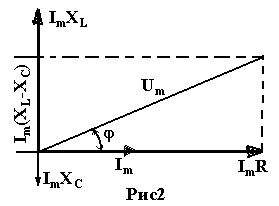Разделив левую и правую часть на корень из 2, получим, что этот закон справедлив и для действующих значений тока и ЭДС. tg - сдвиг фаз между колебаниями тока и напряжения. Из рисунка следует: cos=I_mR_m/U_m=R/Z, что амплитуда тока зависит от частоты колебаний ЭДС. Максимальная амплитуда тока достигается при условии минимума полного сопротивления, т.е. при L-1/C=0. Соответствующая этому частота =(1/CL)^1/2=₀ равна собственной частоте цепи. Итак, максимальная амплитуда тока получается при резонансе. В полной цепи переменного тока необратимые преобразования энергии происходят только на активном сопротивлении R , в то время как величину амплитуды тока ограничивает полное сопротивление Z. Для вычисления активной мощности, т. е средней мощности необратимых преобразований энергии в цепи переменного тока, воспользуемся (1). Подставив получим: P=(1/2)I_m(e_m/Z)R=(I_m/2^1/2)(e_m/2^1/2)(R/Z); R/Z=cos следов.: P=Iecos, cos - коэффициент мощности.  что максимум энергии от источника вынуждающих ЭДС потребляет система, настроенная в резонанс. В этом случае cos=1, а амплитуда тока максимальна.

31.

Система Д.У. квазистационарного электромагнитного поля: , , , (1).Возьмем первое уравнение системы и покажем, что при отказе от условия стационарности это уравнение приходит в противоречие с з-ном сохранения эл заряда. . Возьмем duv от обеих частей , =0 => . Согласно з-ну сохр заряда . В случае стацион полей и квазистац противоречия с з-ном сохр не было. Для стац случая , а для квазистац случая усл-е непрерывности . можно пренебречь. Для квазистац получ-ся . Надо внести коррективы в сис-му(1) если мы переходим к переменному э\м полю.Максвел предложил: (2)гипотеза Максвела. Ур-ние не противоречит з-ну сохр заряда в полной форме. Источником магнитного поля явл-ся токи проводимости и переменное Эл поле. (2) можно переписать . Обозн -плотность тока смещения, тогда (2)переп . Ток смещения не связан с упорядоченным движением зарядов на макроскопическом расстоянии, т е никакого тока в обычном понимании он не представляет. Он хар-т скорость изменения Эл поля, а током назван потому что явл-ся источником эл поля.

Ур-ния М в диф ф.

, , , .(3)

Ур-ния М в инт ф.: , , , (4)

1-е Ур-ния (3)и (4): истоком магнитного поля явл-ся токи проводимости и токи смещения. З-н полгнго тока+ гипотеза Максвелла. З-н полного тока-следствие з-на Ампера. 2-е Ур-ния (3)и (4): источником эл поля явл-ся эл заряды. Выраж-т собой электростат теорему Гаусса-следствие з-на Кулона. 3-е Ур-ния (3)и (4):ист-м эл поля явл-ся переменное магн поле. Ур-ние выр-т з-н э\м индукции. 4-е Ур-ния (3)и (4):Озн-т, что в природе нет магнитных зарядов=> линии магнитного поля нигде не нач-ся и не обрываются. Ур-ние явл-ся следствием з-на Ампера.

Сис-ма ур-ний М хорошо работает в макроскопических масштабах.На микроуровне существенно нач-т проявляться квантовые закономерности и законы классической электродинамики уступают место з-м квант электрод. На макроуровне М электродинамика блестяще подтверждается на опыте.

Часто для описания св-в э\м поля исп-ся Ур-ния второго порядка. Получим их. (5), (6). Возьмем ур-ние М , (7). (7)

в (6): (8). Исп-м формулу . В (8) вместо D подст εЕ и преобразуем с пом (6). (9). (8) и (9) в (8): перепишем (10). Если одновременно совершить преобр и - градиентные или калибровочные преобразования. -произвольная скалярная ф-ция. (11)-калибровка Лоренца. С учетом(11) (10) : (12)- Ур-ни второго порядка для .Для получения Ур-ния второго порядка для исп-м . Исп-я (9) получим , . С учетом калибр. Лоренца получим (13). Уравнения (11), (12) и (13)-искомое д\у второго порядка.

3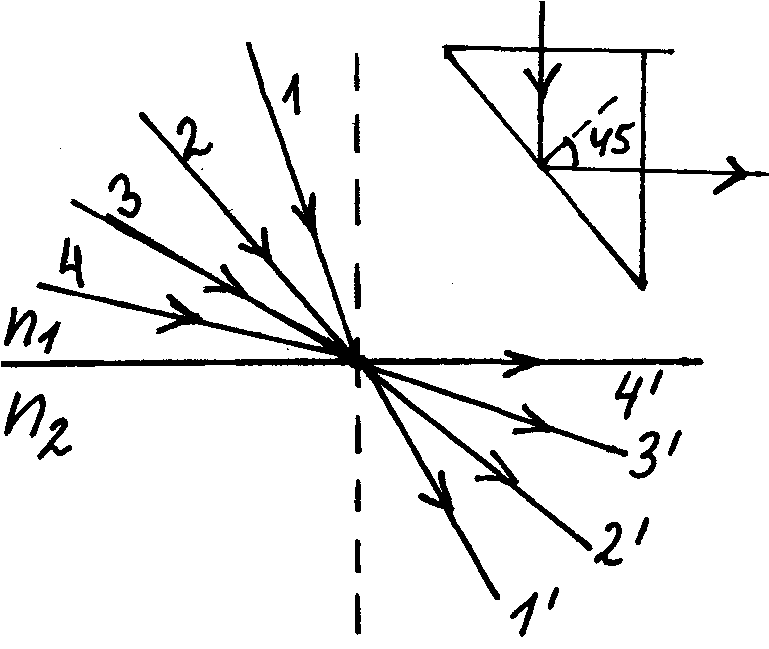 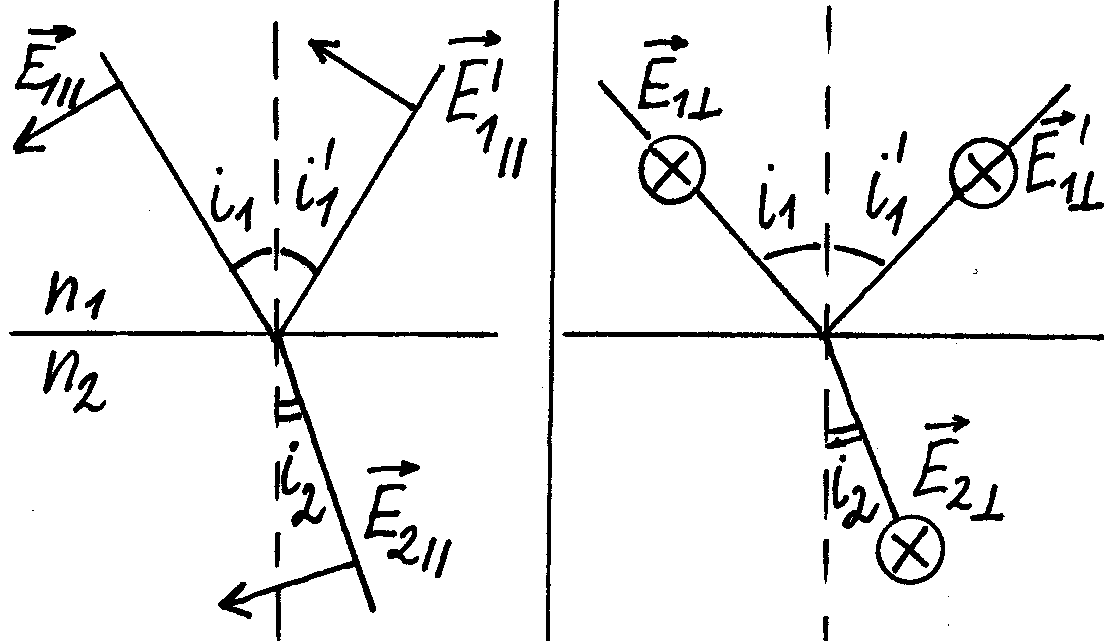2. Прозрачный диэлектрик - не поглощает свет в спектральной интересующей области спектра, хар-ся распространением фазы идеал. монохроматич. волны Е=Е₀Cos(ωt-kx+α). Основной показатель, характеризующий св-ва оптической среды – преломление света. . Чтобы найти интенсивность отраженного и преломленного луча пользуются формулой Френея (опираются на эл магн теорию света). Ф-лы Френеля: любой естественный свет можно представить как совокупность ограниченного количества световых цугов, каждый из которых поляризован линейно, а плоскость поляризации ориентирована хаотически. Вектор напряженности , где -лежит в плоскости падения, -в плоскости перпендикуляр плоскости падения. , - эта система ур-ий показывает связь отраженного и падающего. , - эта система ур-ий показывает связь преломленной и падающей. Поляризация света при отражении. Закон Брюстера: Если естественный световой пучок пустить на границу раздела под определенным углом (Брюстера), то отраженный луч окажется полностью линейно поляризованным (Свет, в котором колебания векторов и каким-либо образом упорядочены, называется поляризованным , где напряженности электрического и магнитного полей). Это потому, что в отраженном пучке исчезает одна из компонент . Для параллельных: ; => ; ; => Т.о. - закон Брюстера. Здесь i_Б – угол полной поляризации, n₁₂ – относительный показатель преломления. Закон Брюстера: Луч света, отраженный от границы раздела двух диэлектриков полностью поляризован, если тангенс угла падения равен относительному показателю преломления той среды, от которой луч отражается. Степень поляризации света: , где . Полное внутренне отражение:

- предельный угол, при котором , , где . Если -то полное внутренне отражение, т.е .

Коэффициенты отражения света: - отношение интенсивностей. Запишем ф-лу Френеля для интенсивностей. Возведем в квадрат и умножим на . Получим: , , = [если свет естественный, то поляризация разная => ]= . Для любого угла мы можем посчитать коэффициент отражения . Коэффициент отражения при нормальных условиях: , , , ;

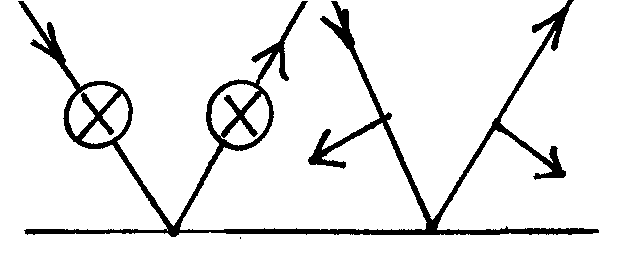= = . Для чистого стекла: , учитывая, что . Для чистого стекла . При очень больших углах падения коэффициент отражения света от чистой границы стремится к 1. Т.е. чистая поверхность становиться похожей на зеркало.

Поведение фазы световой волны при отражении и преломлении. (рис: Е – амплит) Для падающей и отраженной волн: Если волна поляризована перпендикулярно к поверхности падения, то отсутствию скачка фазы при отражении соответствует совпадение значений и . Для волны поляризованной в плоскости падения, скачок отсутствует лишь в том случае, если значения и противоположны. Фазовые соотношения между отраженной и подающей волнами зависит от соотношения между показателями преломления n1 и n2, и от соотношения между углами падения и углом Брюстера. Т.о. если падают под углом < i_Б , то отражение от оптически более плотной среды сопровождается скачком фазы на . От менее оптически плотной среды фаза не меняется.

32(2)

	и знаки одинаковы(скачок на ). и знаки противоположны (скачок на )	и знаки противоположны (скачка нет). и знаки противоположны (скачок на )
	и знаки противоположны(скачка нет). и знаки одинаковы (скачка нет)	и знаки одинаковы (скачок на ). и знаки одинаковы (скачка нет)

Для малых углов падения: и

33. Задачи: 1)светотехника (формирование и расчет световых полей); 2)оптотехника (формирование изображений).Световой луч - линия, которая совпадает с направлением распространения световой энергии. Законы, которым подчиняются световые лучи: 1)Прямолинейности распространения свет луч.(нарушается, когда всплывают волн св-ва и неоднородности в средах); 2)Независимости свет луч: Свет луч при пересечении не влияют друг на друга( нарушается если рассматриваются мощные свет пучки(лазер));

3 )Зеркального отражения :угол отражения = углу падения; падающие, отраженные лучи и нормаль лежат в одной плоскости; 4)Преломления : n=()^1/2, n=c/v, sini₁/sini₂=n₂/n₁ = n₂₁. Все законы являются приближенные и при расчетах надо учитывать поправки. Оптотехника занимается изучением законов формирования изображения предметов. Если пучок выходит из точки либо собирается в точку то называется гомоцентрическим. Если гомоцентричность пучков нарушается, то говорят, что система формирует стигматическое(точечное) изображение. Если изображение форм сами сходящиеся лучи то изображение действительное, если изображение получается на продолжении расходящихся, то мнимое. Сфер зеркала (Р – вершина, О – центр кривизны)- бывают вогнут и выпуклые. Линия через вершину зеркала и центр кривизны –глав оптическая ось. Любая ось проходящая через тчк О наз вспомогательной. Параксиальные лучи - лучи, которые находятся под малым углом к главной оптической оси и на небольшом расстоянии от нее. Малые углы, это если sina=tga=a. В пределах параксиальной оптики отрезком РВ→0 можно пренебречь. Тогда: АP≈AD=a. BP≈BD=b. PO≈DO=r. ₂=i₁+₁, ₃=i₂+₂, ₂-₃=₁-₂ => i₂ = i₁ ; ₁=h/a, ₂=h/r, ₃=h/b. С учетом этого: 1/r-1/b=1/a-1/r => 1/b+1/a=2/r-формула зеркала. Знак отрезка опред-ся по правилу: начало отсчета - вершина зеркала; направление отсчета отрезка от вершины сравнивают с напр-ем падающих лучей, если совпадают, то отрезок положительный. Фокус-это точка, в которой сходятся отраженные от зеркала лучи пущенные парал-но относ-но главной оптической оси. a→∞, b→f, тогда 0+1/f=2/r, f=r/2. C учетом этого ф-ла зеркала: 1/b+1/a=1/f. Плоскость проход через фокус перепенд глав опт оси наз фокаль плоск y’/y=b/a=N—попереч-ое увелич-ие. (Смотри рисунок справа): b=af/(a-f), но a<0 и f<0, то b=af/(f-a), то b<0—изобр действ.Выпукл зерк даёт мнимое прямое и умен изобр., фокус мнимый, покажем это: b=af/(a-f), a<0, f>0, b=-af/(-f-a)=af/(f+a), b>0. Тонкой наз линзу, толщиной которой можно пренебречь по сравнению с радиусом кривизны (рис4) Для тонкой линзы:Ф=1/f=(n/n_ср-1)(1/r₁-1/r₂)-оптическая сила( измеряется в диоптриях. 1 дп - оптическая сила линзы с фокусным расстоянием в воздухе 1 м). Формула тонкой линзы: 1/b-1/a=1/f.(а-расст линза-предмет, b-расст линза-изображение, f-фокусное расст-ие). Собирающие линзы- центральная часть толще переферии. (рис5): N=y’/y=b/a(дает действ перевёр увелич изображение). (рис6):(мнимое, прямое увел b<0). Для рассеивающей линзы (рис7):(фокусы отриц-е и мнимые). С помощью ф-лы тонкой линзы можно показать, что рассеивающая линза всегда дает уменьшенное прямое изображение. b=af/(a-f), a<0 f<0 b=af/(-a-f)=

-af/(a+f), то b=-f/2. Для сист из двух линз Ф=Ф₁+Ф₂. В реальных системах из-за отклонения от параксиальности и монохр-ти стигмат-сть изобр-я нарушается, т.е точка изобр-ся в виде пятна.

Центрированной наз такая оптическая сист, центры кривизны которой находятся на одной линии. Для любой сложной системы вводят 4 кардинальные точки: перед и зад фокус и 2 главные точки. Гл точки- точки пересеч 2-х глав плоскостей с глав оптической осью. Глав плоскости это такие 2 пл-ти перпендикулярные глав оптической оси, каждая точка второй, есть изображающая точек первой с поперечным увел =1. H₁ и H₂ – глав точки. Все расстояния отсчитываются от главных точек. Аберрации оптических систем: Отклонение от пораксиальности и монохромности влияет на нарушение стигматизма (ухудшение четкости, формы и т.д.). 1) Хромотическая аберрация (немонохромотичность лучей) – причина: зависимость n(λ); 2)Связанные с отклонением от параксиальности лучей: а)сферическая аберрация (отклонение лучей, проходящих через кольцевую зону линзы, аберрации у собирающей линзы , у рассеивающей ) – проявляется при широких пучках; 3) Астигматизм - проявляется при узких пучках; 4)Дисперсия – форма изображения не