7. Вычисление объёмов тел вращения.

Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox, вследствие чего образуется тело вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка. На промежутке(a; b) выберем точку x. Сечение, проведенное через эту точку перпендикулярно оси Ox, есть круг площадью S (x) = πf ² (x). Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V.

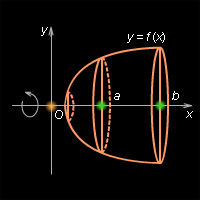
Объем тела вращения равен 

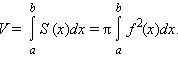
8. Вычисление длин дуг плоских кривых.

Пусть функция f(x) непрерывно дифференцируема на [a,b], тогда длина дуги кривой   на указанном промежутке вычисляется по формуле: Если кривая гладкая и задана параметрически, то длина дуги этой кривой при   вычисляется по формуле: Если гладкая кривая задана в полярных координатах   и  , то длина ее дуги равна

Тема 6. Несобственные интегралы.

1. Несобственные интегралы с бесконечными пределами. Признаки сходимости.

Пусть f (x) является непрерывной функцией в интервале [a, ∞). Несобственный интеграл определяется через предел следующим образом:

Рассмотрим также случай, когда функция f (x) непрерывна в интервале (−∞, b]. В этом случае несобственный интеграл определяется как

Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся.  В противном случае интегралы расходятся.  Пусть f (x) является непрерывной функцией на множестве действительных чисел. Тогда справедливо соотношение

Если для некоторого действительного числа c оба интеграла в правой части сходятся, то говорят, что интеграл   также сходится; в противном случае он расходится. 

Признаки сходимости.

Пусть f (x) и g (x) является непрерывными функциями в интервале [a, ∞). Предположим, что  для всех x в интервале [a, ∞).

Если   сходится, то   также сходится;

Если   расходится, то   также расходится;

Если   сходится, то   также сходится. В этом случае говорят, что интеграл   является абсолютно сходящимся.

2. Несобственные интегралы от неограниченных функций. Признаки сходимости.

Пусть функция f (x) непрерывна в интервале [a,b), но имеет разрыв в точке x = b. В этом случае несобственный интеграл определяется в виде

Аналогично можно рассмотреть случай, когда функция f (x) непрерывна в интервале (a,b], но имеет разрыв при x = a. Тогда

Если приведенные выше пределы существуют и конечны, то говорят, что соответствующие несобственные интегралы сходятся. В противном случае они считаются расходящимися.  Пусть f (x) непрерывна для всех действительных x в интервале [a,b], за исключением некоторой точки  . Тогда справедливо соотношение

и говорят, что несобственный интеграл   сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится. 

Тема 7. Двойные и тройные интегралы.

1. Двойные интегралы. Изменение порядка интегрирования.

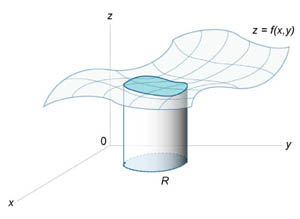
Двойной интеграл от функции f (x,y) обозначается как

где R - область интегрирования в плоскости Oxy. Двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R (рисунок 1).

Рис.1		Рис.2

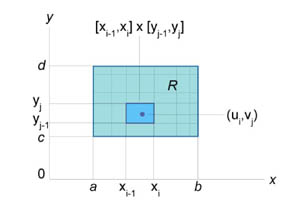
Двойной интеграл от функции f (x,y) в прямоугольной области   определяется как предел суммы Римана, при котором максимальные значения Δx_i и Δy_j стремятся к нулю:

Свойства двойного интеграла

Двойной интеграл обладает следующими свойствами:

, где k - константа;

Если   в области R, то  ;

Если   в области R и   (рисунок 4), то  ;

Если   на R и области R и S являются непересекающимися (рисунок 5), то  .  Здесь   означает объединение этих двух областей.

Изменение порядка интегрирования.

Пример

Дан двойной интеграл   с областью интегрирования  . Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.

Решение: Изобразим область интегрирования на чертеже:   

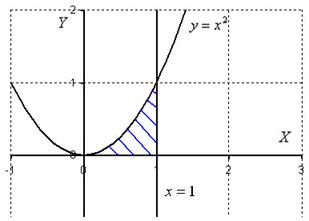
Далее следует найти обратные функции. Единственной функцией, где есть и «икс» и «игрек», является 

Если  , то  , причём: обратная функция   задает правую ветку параболы; обратная функция   задает левую ветку параболы.

Обходим область интегрирования вторым способом:

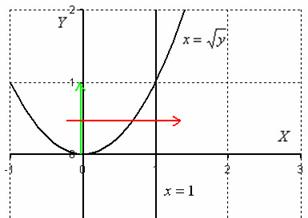
И, следовательно, переход к повторным интегралам таков:

Ответ можно записать следующим образом: