Тема 5. Определённый интеграл.

1. Задачи, приводящие к понятию определённого интеграла. Определённый интеграл как предел интегральных сумм.

Задача о площади криволинейной трапеции

Рассмотрим плоскую фигуру, ограниченную линиями y = 0, x = a, x = b и y = f(x), где f(x) есть непрерывная положительная функция, заданная при a ≤ x ≤ b.

Разделим [a, b] точками a = x₀ < x₁ < x₂ < ... < x_n-1 < x_n = b и пусть λ = max(x_k+1 - x_k). Прямые x = x_k разбивают нашу трапецию на n узких полос. Так как функция f(x) непрерывна, то она мало меняется при x_k ≤ x ≤ x_k+1 и без большой погрешности ее можно считать на промежутке [x_k, x_k+1] постоянной и равной f(ξ_k), где ξ_k есть произвольно взятая точка промежутка [x_k, x_k+1].

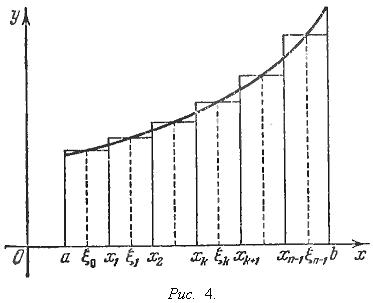
Площадь этой ступенчатой фигуры, очевидно, равна

     Естественно считать, что эта площадь при малом λ является приближенным значением интересующей нас площади F. Поэтому по определению будем называть площадью нашей криволинейной трапеции предел

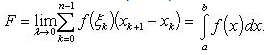
Задача о массе стержня

     Если стержень однороден, то его истинная плотность одинакова во всех его точках и равна его средней плотности. У неоднородного же стержня истинная плотность p меняется от точки к точке. Если определять положение каждой точки M стержня с помощью расстояния x ее от одного из концов стержня (см. рис. 1), то его плотность p в точке x будет функцией от x, p = p(x). Поставим задачу, как, зная эту функцию и длину l стержня, найти его массу m.

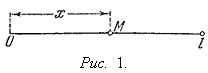
     При решении этой задачи будем считать плотность p(x) непрерывной функцией. Переходя к решению, разделим стержень точками x₁ < x₂ < ... <x_n-1 (0 < x_k < l) на n небольших участков (см. рис. 2).

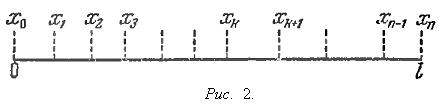
Для единообразия обозначений положим еще x₀ = 0, x_n = l, и пусть λ есть наибольшая из разностей x_k+1 - x_k. Отдельный участок [x_k, x_k+1] стержня приближенно можно считать однородным [т. к. из-за его малости (непрерывная) функция p(x) не успевает на нем сколько-нибудь заметно измениться]. Делая такое допущение, мы тем самым принимаем плотность p(x) на участке [x_k, x_k+1] за постоянную. Пусть значение этой постоянной есть p(ξ_k), где ξ_k есть произвольно выбранная точка участка [x_k, x_k+1]. Тогда масса участка [x_k, x_k+1] будет равна p(ξ_k)(x_k+1 - x_k), а полная масса стержня будет

     Полученное выражение массы является, однако, лишь приближенным, т. к. на самом деле отдельные участки стержня не однородны. Тем не менее, чем короче эти участки, т. е. чем меньше число λ, тем более точным будет найденное выражение m. Отсюда следует, что точное значение массы таково:

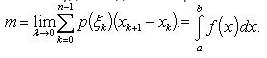
2. Основные свойства определённого интеграла.

Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b].

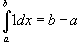
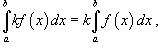 где k - константа;

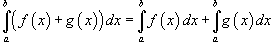
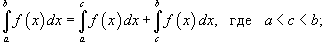
Если   для всех  , то  .

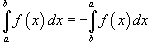
Если   в интервале [a, b], то 

3. Формула Ньютона-Лейбница.

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a,b], то

4. Вычисление определённого интеграла методом замены переменной.

Определенный интеграл   по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):

Новые пределы интегрирования по переменной t определяются выражениями

где g ^-1- обратная функция к g, т.е. t = g ^-1 (x). 

5. Вычисление определённого интеграла интегрированием по частям.

В этом случае формула интегрирования по частям имеет вид:

где   означает разность значений произведения функций uv при x = b и x = a. 

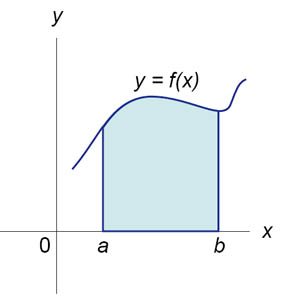
6. Вычисление площадей плоских фигур .

Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функцииf (x) (рисунок 1), определяется по формуле

Рис.1		Рис.2

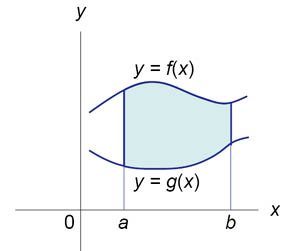
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой