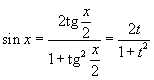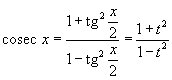5. Интегрирование рациональных дробей.

Для интегрирования рациональной функции  , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:

1. Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;

2. Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

3. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

4. Вычислить интегралы от простейших дробей.

Рассмотрим подробно шаг 3. Разложение рациональной дроби на сумму простейших дробей.

Запишем рациональную функцию в следующем виде:

Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x).  Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов. 

6. Интегрирование иррациональных функций.

Для интегрирования иррациональной функции, содержащей   используется подстановка  .  Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме  , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.  Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида  , интегрируется с помощью подстановки  . 

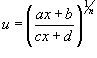7. Дифференциальный бином.

В математическом анализе дифференциальным биномом или биномиальным дифференциалом называется интеграл вида

где m, n, p, a, b — действительные числа.

Дифференциальный бином выражается в элементарных функциях только в трёх случаях:

 — целое число. Используется подстановка  ,   — общий знаменатель дробей   и  ;

 — целое число. Используется подстановка  ;

 — целое число. Используется подстановка  ,   — знаменатель дроби  .

8. Интегрирование тригонометрических функций.

Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции используя универсальную тригонометрическую подстановку x = 2arctg t (или  ).  Для преобразования рациональных выражений от sin x, cos x, tg x, ctg x, sec x и cosec x в алгебраические рациональные функции переменной t применяются следующие тригонометрические формулы:

1. Интегралы вида 

Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность:

2. Интегралы вида 

Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:

1. Если степень косинуса n - нечетная (при этом степень синуса m может быть любой), то используется подстановка  .

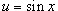2. Если степень синуса m - нечетная, то используется подстановка  .

3. Если степени m и n - четные, то сначала применяются формулы двойного угла

чтобы понизить синуса или косинуса в подынтегральном выражении. Затем, если необходимо, применяются правила a) или b).

3. Интегралы вида 

Степень подынтегрального выражения в данном интеграле можно понизить с помощью тригонометрического соотношения   и формулы редукции

4. Интегралы вида 

Здесь степень подынтегрального выражения понижается с помошью соотношения   и формулы редукции

5. Интегралы вида 

Данный тип интеграла упрощается с помощью следующей формулы редукции:

6. Интегралы вида 

Аналогично предыдущим пунктам, интеграл упрощается с помощью формулы

7. Интегралы вида 

1. Если степень секанса n - четная, то c помошью соотношения   секанс выражается через тангенс. При этом множитель   отделяется и используется для преобразования дифференциала. В результате весь интеграл (включая дифференциал) выражается через функцию tg x.

2. Если обе степени n и m - нечетные, то отделяется множитель sec x tg x, необходимый для преобразования дифференциала. Далее весь интеграл выражается через sec x.

3. Если степень секанса n - нечетная, а степень тангенса m - четная, то тангенс выражается через секанс с помощью формулы  . Затем вычисляются интегралы от секанса.

8. Интегралы вида 

1. Если степень косеканса n - четная, то c помошью соотношения 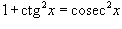  косеканс выражается через котангенс. При этом множитель   отделяется и используется для преобразования дифференциала. В результате подынтегральная функция и дифференциал выражаются через ctg x.

2. Если обе степени n и m - нечетные, то отделяется множитель ctg x cosec x, необходимый для преобразования дифференциала. Далее интеграл выражается через cosec x.

3. Если степень косеканса n - нечетная, а степень котангенса m - четная, то котангенс выражается через косеканс с помощью формулы  . Далее вычисляются интегралы от косеканса.