3. Дифференцирование сложной функции.

Если z = f(x; у) — дифференцируемая в точке М(х;у) D функция и х = x(t) и у =y(t) — дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле

4. Дифференцирование неявной функции.

Пусть уравнение   определяет   как неявную функцию от х.

а) продифференцируем по х обе части уравнения  , получим уравнение первой степени относительно  ;

б) из полученного уравнения выразим  .

Пример: .

5. Касательная плоскость и нормаль к поверхности.

Касательная плоскость к поверхности в её точке   (точка касания) есть плоскость, проходящая через  и содержащая в себе все касательные, проведённые в точке   ко всевозможным кривым, проведённым на поверхности через точку 

Нормалью к поверхности в точке   называется прямая, проходящая через точку   и перпендикулярная к касательной плоскости, проведённой в этой точке.

Уравнение касательная плоскости и нормали к поверхности.

6. Производная по направлению.

Под производной функции u = f (x, y, z) в данном направлении   понимается выражение   =  cosa +  cosb +  cosg, где cosa, cosb, cosg – направляющие косинусы вектора 

7. Градиент функции.

Пусть в каждой точке некоторой области   задана функция  . Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции   и обозначается   или   (читается «набла у»): 

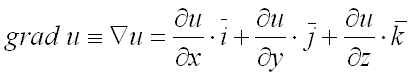При этом говорят, что в области   определено векторное поле градиентов.

Для нахождения градиента функции   в заданной точке   используют формулу: .

 

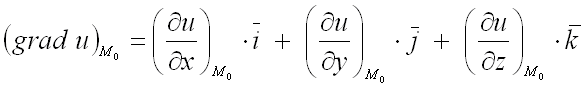Свойства градиента

1. Производная в данной точке по направлению вектора   имеет наибольшее значение, если направление вектора   совпадает с направлением градиента. Это наибольшее значение производной равно  .

2. Производная по направлению вектора, перпендикулярного к вектору  , равна нулю.

8. Понятие экстремума функции двух переменных.

Говорят, что функция   имеет максимум в точке  , т.е. при   , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Говорят, что функция   имеет минимум в точке  , т.е. при  , если   для всех точек  , достаточно близких к точке   и отличных от неё.

9. Необходимое условие экстремума функции двух переменных.

Если функция   достигает экстремума при  , то каждая частная производная первого порядка от   или обращается в нуль при этих значениях аргументов, или не существует.

10. Достаточное условие экстремума функции двух переменных.

Пусть в некоторой области, содержащей точку   функция   имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка   является критической точкой функции  , т.е. 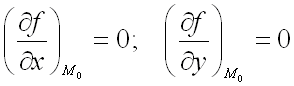, тогда при  : 1)   имеет максимум, если дискриминант   и  , где 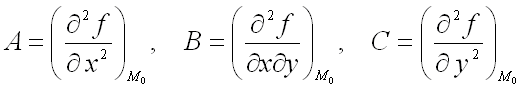 ; 2)   имеет минимум, если дискриминант   и  ; 3)   не имеет ни минимума, ни максимума, если дискриминант  ; 4) если   , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

11. Наибольшее и наименьшее значения функции в замкнутой области.

Пусть в замкнутой области D задана функция z=z(x,y), имеющая непрерывные частные производные первого порядка. Тогда в области D функция z(x,y) достигает своего наибольшего M и наименьшего m значений.

Можно предложить следующий план нахождения M и m.  1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы.  2. Находим стационарные точки внутри D.  3. Находим стационарные точки на каждой из границ.  4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения. 

ТЕМА 4. Неопределённый интеграл.

1. Первообразная и неопределённый интеграл.

Функция F(x) называется первообразной функции f(x), если

Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как

Таким образом, если F - некоторая частная первообразная, то справедливо выражение

где С - произвольная постоянная. 

2. Основные свойства интеграла.

В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,  а, k, C - постоянные величины.

3. Интегрирование по частям

Пусть u(x) и v(x) являются дифференцируемыми функциями. Дифференциал произведения функций u и v определяется формулой

Проинтегрировав обе части этого выражения, получим

или, переставляя члены,

Это и есть формула интегрирования по частям. 

4. Интегрирование методом подстановки.

Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением

где x = g (u) - подстановка. Соответственно, обратная функция u = g ⁻¹(x)описывает зависимость новой переменной от старой.  Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du.