6. Исследование функции на выпуклость и вогнутость. Точки перегиба функции. Теорема о существовании выпуклости, вогнутости.

Кривая называется выпуклой (вогнутой), если все точки этой кривой расположены ниже (выше) любой касательной, проведённой к этой кривой

Пусть функция y=f(x) в некоторой окрестности т. Xo и дважды дифферен. в этой точке. Тогда если при переходе через эту точку f’’(x) меняет свой знак, то точка Xo называется точкой перегиба (в этой точке выпуклость меняется на вогнутость).

Если функция y=f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство   ( ), то график функции имеет выпуклость направленную вниз (вверх) на Х.

7. Теоремы о необходимом и достаточном условии существования точек перегиба.

Пусть функция y=f(x) дважды дифферен. в точке Xo. Тогда если точка Xo является точкой перегиба, то f’’(x)=0.

Пусть функция y=f(x) определена и непрерывна в некоторой окрестности т. Xo и дважды дифферен. в этой окрестности. Пусть f’’(x)=0 в этой точке. Тогда, если при переходе через эту точку f’’(x) меняет свой знак, то эта точка является точкой перегиба.

8. Асимптоты кривой.

Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю при неограниченном удалении от начала координат.

Вертикальные асимптоты ищутся в точках разрыва функции. Если в точке Xo существует разрыв 2 рода, то прямая X=Xo является вертикальной асимптотой.

Наклонные асимптоты: y=f(x); y=ax+b

;

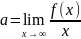Если один из коэффициентов а или b равен бесконечности или не существует, то наклонных асимптот нет.

Горизонтальные асимптоты.

В случае а=0, то y=b. Если а=0, то горизонтальная асимптота может иметь место. Но если b≠ и b=y, то это горизонтальная асимптота.

Тема 3. Дифференцирование функций нескольких переменных.

1. Частные производные и полный дифференциал функции двух переменных.

Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

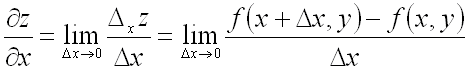Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

Полным дифференциалом функции z=f(x,y) называется главная часть полного приращения     , линейная относительно приращений её аргументов  . Полный дифференциал функции (если он существует) равен сумме всех ее частных дифференциалов и вычисляется по формуле:

При достаточно малых (по абсолютному значению) приращениях аргументов, полное приращение функции можно с как угодно малой относительной погрешностью заменить ее полным дифференциалом. Дифференциалы dх и dy независимых аргументов функции х и у совпадают с их приращениями соответственно     . Таким образом,

2. Частные производные и дифференциалы высших порядков функции двух переменных.

Частные производные высших порядков.

Частные производные функции двух переменных z=f(x,y) являются функциями переменных x и y. Поэтому их снова можно дифференцировать. Так как каждую функцию z_x^/и z_y^/можно дифференцировать по x и y, то производных второго порядка будет четыре. Производные второго порядка можно снова дифференцировать по x или по y.

Частная производная n-го порядка, есть первая производная от производной (n-1)-го порядка. 

Дифференциалы высших порядков

Если функция    имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .

Символически общий вид дифференциала n-го порядка от функции   выглядит следующим образом:

где  , а    произвольные приращения независимых переменных  . Приращения    рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.