Ответы для подготовки к экзамену по дисциплине «Высшая математика» (II семестр) тема 1. Дифференциальное исчисление функции одной переменной.

1. Производная функции одной переменной, её геометрический и физический смысл.

Рассмотрим функцию f(x), область определения которой содержит некоторый открытый интервал вокруг точки x0. Тогда функция f(x) является дифференцируемой в точке x0, и ее производная определяется формулой

Геометрический смысл производной: производная f'(x0) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x0, который в свою очередь равен tg угла наклона касательной к графику функции.

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

2. Непрерывность функции одной переменной, имеющей конечную производную.

Теорема. Если функция    дифференцируема в некоторой точке  a, то она непрерывна в этой точке.  Доказательство. По определению производной

Это предельное равенство означает, что выражение под знаком предела можно представить в виде

где  α(x)  – бесконечно малая функция при  x → a. Тогда

Следовательно,     при  x → a. 

3. Уравнение касательной и нормали к графику.

Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x0, y0), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy.

Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x0), то получаем уравнение y= f'(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f'(x0)·x0 + b. Отсюда b=y0– f'(x0)·x0.

Таким образом, получаем уравнение касательной y= f'(x0)·x +y0 – f'(x0)·x0 или y = f '(x0)·(x – x0) + f(x0)

Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.

Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством:

Учитывая, что нормаль также как и касательная проходит через точку M(x0, y0), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:

.

4. Теоремы о производной суммы, разности, произведения и частного двух функций одной переменной.

Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы:

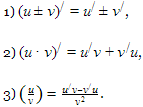
5. Производная сложной функции.

Сложная функция – это функция, аргументом которой также является функция.

Сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна

Формула нахождения производной сложной функции.

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x).

6. Производная обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах   и   соответственно. Если в точке   существует конечная отличная от нуля производная функции f(x), то в точке   существует конечная производная обратной функции g(y), причем  .