12 Надежность (безотказность) невосстанавливаемого изделия, функция надежности

Вероятность безотказной работы любого изделия связана с безотказной работой комплектующих его элементов. Под элементом изделия понимают не только неделимая часть изделия, но и любое устройство надежность которого рассчитывается не зависимо от надежности других элементов.

Функция надежности.

П редположим, что имеется элемент, которые прошел приработку, т.е. все приработочные отказы устранены. Известно, что в момент включения он исправен, момент включения считаем за начало отсчета наработки, очевидно, что в вероятность достоверного события будет равна 1: .

С течение наработки вероятность безотказной работы уменьшается – это объясняется тем, чем больше времени работает элемент, тем больше вероятность того что произойдет отказ либо за счет случайной концентрации нагрузок, либо в результате старения (износа). Если внезапный отказ не произошел, то износовый произойдет обязательно. Будем считать что элемент может находится в двух состояниях – работоспособном и неработоспособном.

Пусть событие А – это событие заключающееся в точ, что элемент находится в работоспособном состоянии, а В – это событие заключающееся в том что элемент находится в состояние отказа. Тогда поскольку событие А+В – полная картина событий, поэтому эти события противоположны: Р(А)+Р(В)=1 (1). Вероятность безотказной работы элемента по времени будем обозначать P(t), вероятность отказа Q(t). Тогда (1) P(t)+ Q(t)=1 (2).

Равенство (2) определяет общую надежность элементов.

К ривую P(t) называют функцией надежности или законом надежности, Кривую Q(t) – функцией ненадежности. Функцию безотказности можно найти приближенно из опыта. Для этого необходимо взять большое число одинаковых элементов, включив их в работу, отмечать моменты появления отказов в течение заданного времени. Зная эти моменты определить функцию P(t) = число элементов оставшиеся неотказавшимися к моменту времени t.

В начальный момент времени n(0)=N. В момент каждого отказа эта функция уменьшается на 1, если разделить число элементов оставшиеся работать на число элементов, поставившихся на испытание: . , при t=0 P_N(0)=1, при t=t_n P_N(t_n)=0.

При увеличении числа испытываемых элементов эта функция приближается к функции P(t). , .

13 Интенсивность отказов, общая формула вероятности безотказной работы

Интенсивность отказов ( ) называется вероятность отказа не ремонтируемого изделия в единицу времени при условии, что отказ до этого момента не возникал. Предположим, что некоторый элемент проработал в течение интервала времени от 0 до t. Какова вероятность того, что этот элемент откажет на интервале .

А-событие безотказной работы от 0 до t. В-событие безотказной работы от t до t₁.

Для того чтобы элемент смог безотказно работать на интервале он должен безотказно проработать на интервале 0 до t.

Р(АВ)=Р(А)*Р(В/А) (1)

Р(А) =Р(0,t) – вероятность безотказной работы элемента на интервале от 0 до t.

Р(В/А) = Р(t,t₁) – условная вероятность события В, что условие А имело место.

Р(В/А)= Р(t,t₁)=Р(АВ)/Р(А); Р(АВ)= Р(0,t₁).

0, t= 0,t+ t, t₁,

Р(t,t₁)= Р(0,t₁)/ Р(0,t) (2)

Р(t,t₁)= Р(t₁)/ Р(t) (2а)

Вероятность отказа элемента на интервале (t, t₁):

Равенство (3) может быть переписано в виде: . Умножим числитель и знаменатель (4) на при .

, , введем обозначение - интенсивность отказа.

Из равенства (5) с учетом (6) получим: , .

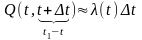Из (7) следует что интенсивность отказа есть отношение вероятности отказа на интервал ( ) при . Интенсивность отказов определяемая (7) стремится к интенсивности отказа определяемая равенством (6). В соответствии (6) величина может быть определена из графика функции надежности как отношение численного значения тангенса угла наклона касательной к кривой к численной ординаты функции надежности.

Если известна интенсивность отказа элементов, то можно рассчитать вероятность работы любой сколь угодно сложной системы. Незнание функции для составляющих элементов исключает возможность определить вероятность безотказной работы.

Чем менее точно известно для элементов тем больше ошибки в расчете безотказности изделия.

Интенсивность отказов может быть определена опытным путем на основе испытаний изделий.

Предположим Р(t) – есть отношение: , - число элементов, оставшихся безотказными. Тогда на малом отрезке и большом числе испытуемых образцов N.

, , ,

где -число отказавших элементов на интервале времени, n(t)-число неотказавших элементов.

Э кспериментальная кривая заменяется плавной кривой. Чем больше N и меньше интервал времени , тем точнее экспериментальная характеристика и заменяющая её плавная кривая, которая отражает действительную картину интенсивности отказов.

Эргодическая теория. На основании известной из теории вероятности эргодической теории среднее значение (мат. ожидание) при совокупном наблюдении ……….равна среднему значению по времени, определенной за одной системой (элементов).

В данном случае это означает, что изменение интенсивности отказа по времени для 1-го отдельно взятого элемента может быть описано тем же самым законом что и интенсивность, полученная при испытании однотипных элементов большой группы.

Вид функции показан 3 характерных участка:

I – участок приработки; II – нормальной эксплуатации; III – участок износовых отказов, могут возникать внезапные отказы.

Деление на участки является условным но оно позволяет рассмотреть работу элементов по участкам и для каждого участка применять свой закон распределения.

, -общая формула безотказной работы позволяет определить Р если известна интенсивность отказа.

Если требуется определить вероятность безотказной работы . Равенство (12) справедливо при условии, что в момент времени t₁ элемент находился в работоспособном состоянии.