5 Равномерное распределение плотности вероятности

Д анное распределение справедливо в том случае, если случайное событие лежит в определенном интервале времени от до и появление его в этом интервале равновероятно. Поскольку событие произойдет на интервале времени отсюда вероятность его появления: , а . Функция распределения: . Математическое ожидание случайной величины будет определяться величиной: , а дисперсия . Дисперсия случайной величины при равномерном распределении растет пропорционально квадрату интервала. Это распределение равномерно.

Г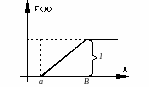 еометрическая интерпретация математического ожидания это координата центра тяжести плоской фигуры, ограниченной прямой плотности распределения и абсцисса. Дисперсия это момент инерции плоской фигуры относительно оси, проходящей параллельно оси плотности распределении через центр тяжести.

6 Нормальное (Гауссово) распределение плотности вероятности

Н ормальное распределение используется в теории вероятности для описания событий, зависящих от многих факторов, каждый из которых слабо влияет на распределение случайных событий. По нормальному закону распределяются параметры серийной продукции, параметры износа. Плотность распределения: .

Распределение Гаусса зависит от двух параметров М(х) и Д(х). Кривая плотности симметрична относительно оси, параллельной оси ординат. Максимальное значение этой плотности равно . Вероятность попадания случайной величины распределенной по нормальному закону в заданный интервал : . Для упрощения расчета используется табулированное выражение равенства (2), вводим новую переменную , тогда , . . - интеграл Лапласа или интеграл вероятности, тогда . Интеграл вероятности обладает свойствами: Ф(0)=0, Ф( )=0,5, Ф(-х)=-Ф(х).

При нормальном распределении на интервале 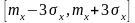срабатывает закон 3 , согласно которому в этом интервале попадание почти 100%, 97,7%, поэтому вероятность появления случайной величины вне этого интервала очень мала, менее 0,3%.

7 Показательное распределение случайных величин

Это распределение является наиболее распространенным в технике из-за своей простоты. Он дает информацию о распределении отказов техники, имеющей многоэлементную структуру. Функция распределения показательного закона выглядит следующим образом: , .

Дисперсия: , . Свойство (3) часто используется как основное свойство показательного закона (в качестве грубой оценке возможности применения показательных возможностей её применения на основе полученных экспериментальных данных)

8 Закон распределения Рэлея, Вейбулла и Пуассона

Рэлея. Во многих прикладных задачах случайные величины могут принимать только положительные значения, в этом случае величины подчиняются закону распределения Рэлея: . В этом случае плотнотсь распределения будет определяться: .Математическое ожидание: . Распределение Релея является однопараметрическим, так как математическое ожидание и дисперсия связана соотношением (3). Распределение Релея используется для ????? вероятностных характеристик колебательных процессов, когда амплитуда принимается положительная, вибрационные процессы описываются распределением Релея.

Вейбулла. При изучение надежности технических систем часто используется распределение Вейбулла. В основном этот закон используется при описании разбросов усталостной прочности стальных конструкций, конструкций из сплавов.

Функция распределения: , если к=1 – показательный закон распределения.

З акон зависит от и к.

Плотность распределения: . Согласно (2) закон распределения Вейбулла зависит от k.

Пуассона. Данное распределение является дискретным и им часто пользуются для определения вероятности потока событий. Дискретная случайная величина Х (безразмерная) называется распределенной по закону Пуассона если её возможные значения равны 0, 1, 2, 3…n, а вероятность того, что x=n определяется по формуле: , Распределение Пуассона обладает тем свойством, что и мат. Ожидание и дисперсия равны одной и той же величине.