35 Сокращение времени непрерывной работы

Данный метод не является методом повышения надежности, так как повысить надежность путем варьированием времени _____________________. Сократить время непрерывной работы системы можно при однократном включении и выключении. Рассмотрим какой эффект ___________________

____________________________________________________ при этом предполагаем, что справедлив экспоненциальный закон надежности.

Вероятность безотказной работы P₁(t) и P₂(t)- идентичных систем для непрерывной работы P₁(t), P₂(t)-дискретной работы.

, К- коэффициент, показывающий во сколько раз время работы 2 системы меньше 1.

. Сравнивая (2) с предыдущим выражением по вероятности отказа. Это означает, что сокращение времени непрерывной работы эквивалентно _____________ числу раз интенсивности отказа. Особенно большой эффект сокращения времени непрерывной работы дает при резервировании систем.

Из графика следует, что при большом T=t вероятность P₂(t) и P₁(t) различаются незначительно P₁(t)≈ P₂(t) и выигрыш надежности мал. Если уменьшить , то вероятность безотказной работы системы (кривая А) значительно выше непрерывистой системы (кривая В). . Подобный эффект основывается на основном противоречии. Выигрыш надежности резервированной системы тем выше, чем меньше время её непрерывной работы.

36 Уменьшение среднего времени восстановления

Время восстановления не влияет на основные количественные характеристики надежности, но оно оказывает влияние на коэффициенты готовности, вынужденного простоя, частоту профилактики.

Выводы:

1.Наиболее эффективным методом повышения надежности сложных систем для кратковременной работы – резервирование;

2.Уменьшение интенсивности отказов изделия наиболее надежный метод для сложных систем длительного пользования.

Сложная система(изделие): уменьшение интенсивности (сложная длительное врем работы); резервирование (кратковременная).

37 Спектральный метод расчета надежности при перемежающихся отказах

Во всех предыдущих методах расчета надежности предполагалось, что параметры элементов изделия с течением времени изменяются монотонно, такое изменение параметров происходит в следствии старения и износа – этот процесс происходит достаточно медленно и в процессе эксплуатации системы приводит к износу её характеристик. В практике случаются случаи перемежающихся отказов. Последние хотя и длятся короткое время могут приводить к нарушению функций. Причинами перемежающихся отказов – флуктуационные изменения параметров возникают из-за случайных ____________________________________________________________________________.

Рассмотренные выше методы надежности не применимы для случая, когда возникают перемежающие отказы. Расчет надежности в этом случае можно выполнить, что если изменение параметров во времени есть стационарный случайный процесс. При таком предположении выходные характеристики представляются в виде случайных функций, удовлетворяющих условиям верх. процесса.

Если дано 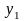и , то при условии когда - условие возникновения отказа. Среднее число выбросов функции за пределы , :

, дисперсия выходной характеристики; производная от корреляционной функции ,где корреляционная функция .

По средней частоте отказа можно определить остальные характеристики с помощью известных формул.

Если поток выбросов простейший, то справедлив экспоненциальный закон надежности: . Если распределение амплитудного процесса нормальное, то расчет приходится вести_________________

______________________________________________________________________________________

Из (1) видно, что для необходимо найти и эти величины находятся если известны комплектующие параметров.

Если предположить, что корреляционные связи между параметрами отсутствуют и их отклонение относительно средних величин малы, то , где n – число пар. элементов системы, которые определяют выходную характеристику . При известных зависимостях изменения параметров во времени можно найти через спектральную плотность (Sj):

, где и - спектральная плотность и корреляционная функция случайного процесса изменения j-го элемента.

При известной реализации процесса спектральную плотность можно вычислить с помощью коррелятора.

При аналитическом способе первоначально вычисляются корреляционна функция, затем она аппраксимируется и вычисляется спектральная плотность и с помощью преобразования Фурье определяется величина: . На основе(2) и (3): , . Тогда корреляционная функция может быть определена по спектральной плотности с помощью обратного преобразования Фурье: . Спектральный метод расчета практически дает возможность аналитически _________ при условии когда имеется ограниченное число параметров. Удобно применять для простых систем. Но с ростом числа элементов в сумме 5- с использованием ЭВМ.

Недостатки:

1. Метод не учитывает корреляционные связи между параметрами;

2. Трудность вычисления основных характеристик надежности в случае если поток отказа не является простейшим. В этом случае частота отказа будет функцией времени если поток параметров не стационарен.

3. Метод не позволяет учитывать влияние внезапных и постепенных отказов на перемежающиеся отказы.

40