
11. Вычислить интеграл
а)
 , б)
, б)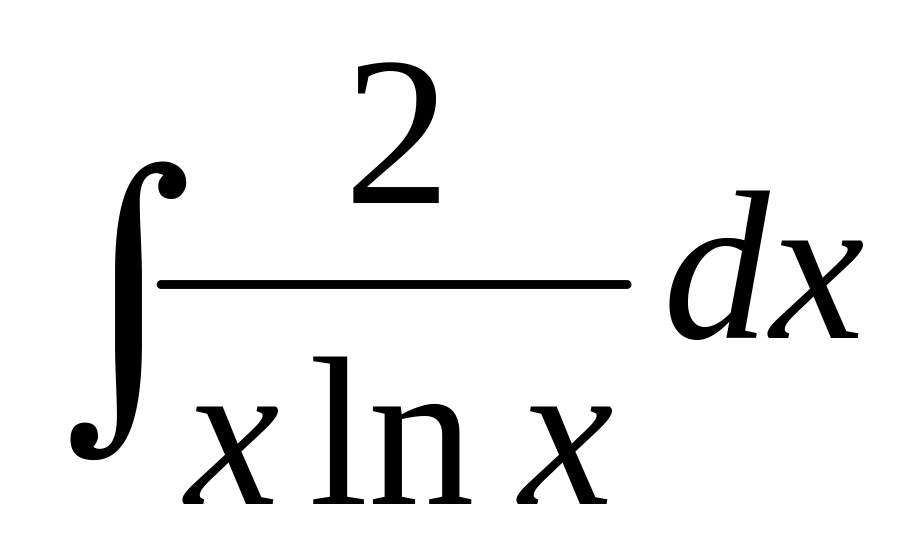 ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б) ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б)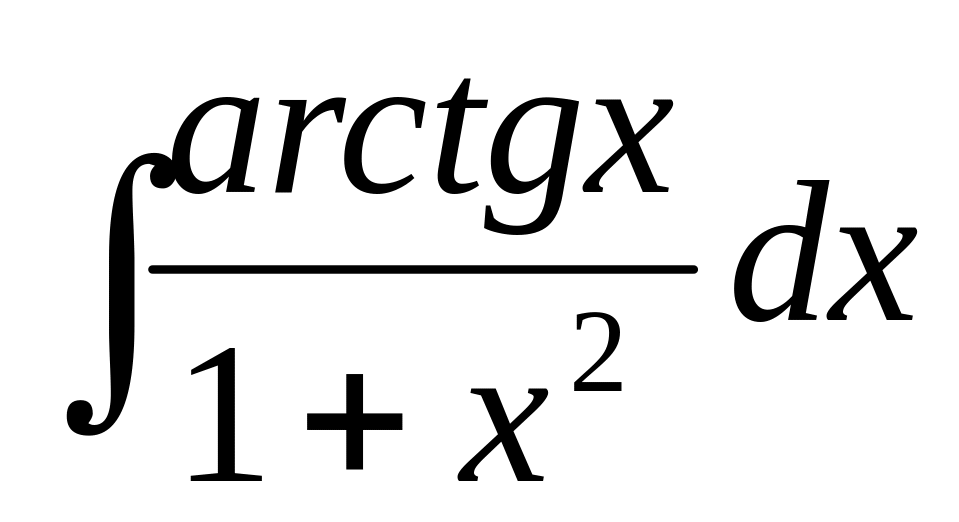 ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б) ,
,
в)![]() , г)
, г)![]() ;
;
а)
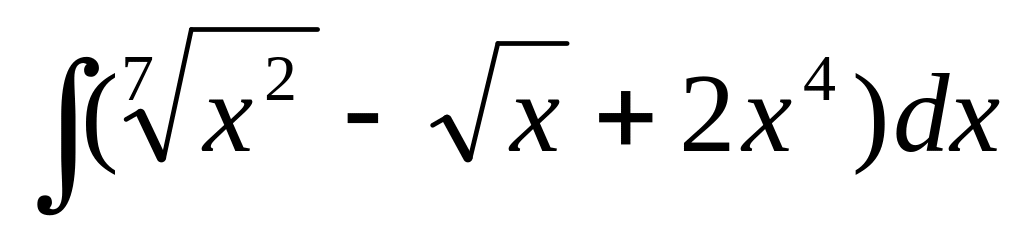 , б)
, б)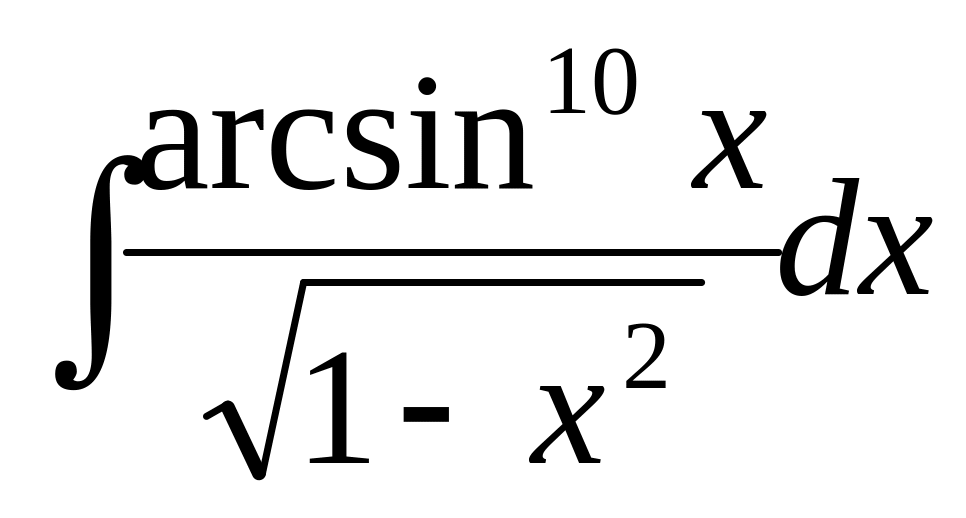 ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б)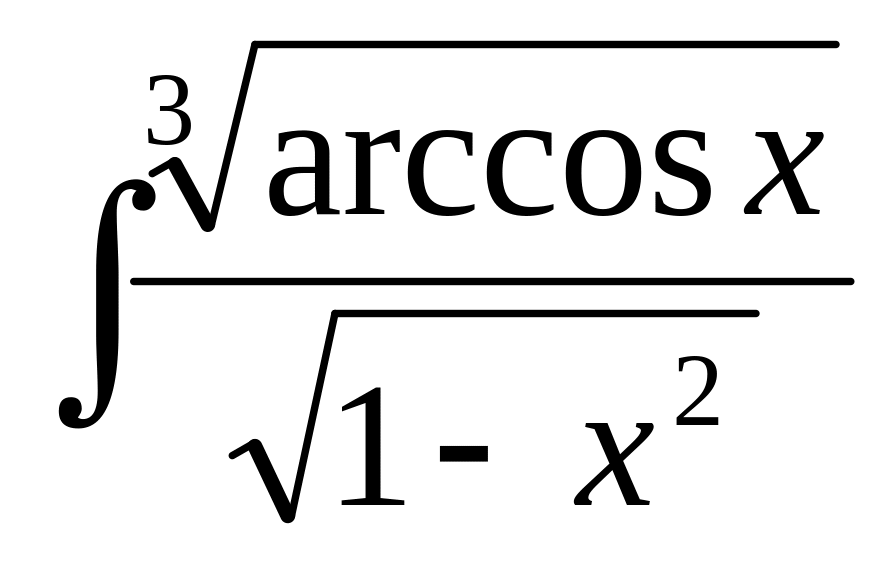 ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б) ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б) ,
,
в)![]() , г)
, г)![]() ;
;
а)
 , б)
, б) ,
,
в)![]() , г)
, г)![]() ;
;
а)
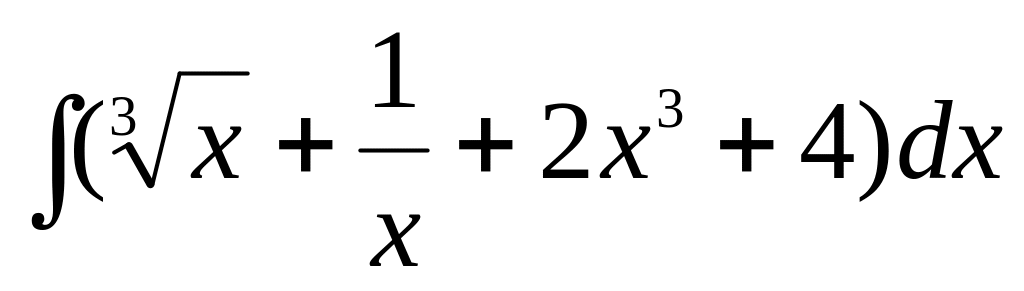 , б)
, б) ,
,
в)
![]() , г)
, г)
![]() .
.
12. Вычислить интеграл.
1.
![]() ;
2.
;
2.
![]() ;
;
3.
![]() ; 4.
; 4.
![]() ;
;
5.
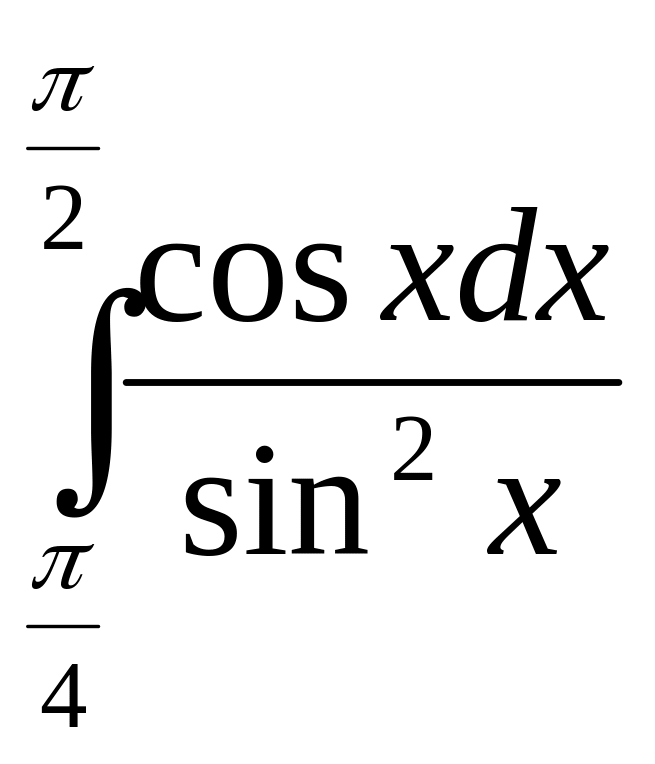 ;
6.
;
6.
 ;
;
7.
 ;
8.
;
8.
 ;
;
9.
![]() ; 10.
; 10.
![]() .
.
13. Найдите площадь фигуры, ограниченной линиями
 .
. .
. .
. .
. .
.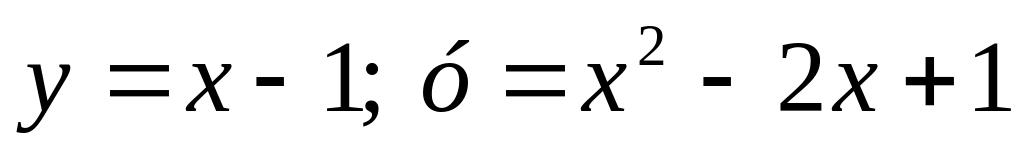 .
. .
. .
.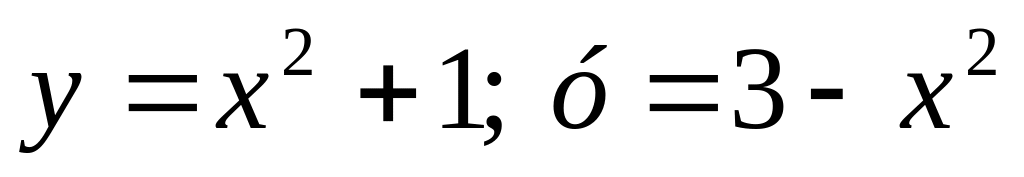 .
. .
.
Литература
1. Письменный Д. Конспект лекций по высшей математике. - М.: Айрис, 2001.
2. Гусак А.А. Высшая математика в 2-х томах. - М.: Терра-систем, 2001.
3. Минорский В.П. Сборник задач по высшей математике. М., Наука, 1970.
4. Данко П. Е. и др. Высшая математика в упражнениях и задачах в 2-х томах. М., Высшая школа, 2001.
5. Пискунов Н.С. Дифференциальное и интегральное исчисление в 2-х томах. М., Наука, 1985.
6. Берман Г.Н. Сборник задач по курсу математического анализа. М., Наука, 1985.
7. Бугров Я.С., Никольский С.М. Высшая математика. М, Наука,2000.
Каверин С.В., Скрябина Е.С Линейная алгебра: Учебно-методическое пособие. Ч.1 . - Тольятти: ВУиТ, 2006. - 49 с
Скрябина Е.С. Линейная алгебра. Аналитическая геометрия. Дифференциальное исчисление: Учебно – методическое пособие. Ч. 1. – Тольятти: Волжский университет им. В.Н. Татищева, 2004. – 46 с.
Скрябина Е.С. Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения. Ряды: Учебно – методическое пособие. Ч. 1. – Тольятти: Волжский университет им. В.Н. Татищева, 2004. – 37 с
Высшая математика в задачах и упражнениях: Учебное пособие / О. Н. Иванов, Н. Г. Бабенко, А. Н. Ярыгин, О. Н. Ярыгин. - Тольятти : ВУиТ, 2004. - 82 с
Приложения
ВОЛЖСКИЙ УНИВЕРСИТЕТ ИМЕНИ В.Н.ТАТИЩЕВА
Кафедра
Прикладная математика
Контрольная работа по математике
Вариант № ________
Выполнил:
студент 1 курса группы ____
Ф.И.О.___________________
Проверил:
__________________________
Тольятти 2012
Приложение 1
Основные соотношения и формулы элементарной математики
Обыкновенные дроби
![]()
Пропорции Степени и корни
![]()
![]()
Действия
со степенями и корнями (![]() >0)
>0)

Формулы сокращенного умножения
![]()
Квадратное уравнение
![]()
![]()
Разложение
квадратного трехчлена на множители
(D≥0)
![]() .
.
Теорема
Виета:
![]()
Логарифмы
Логарифм числа
![]() по основанию
по основанию
![]() :
:
![]()
![]() - основное
логарифмическое тождество
- основное
логарифмическое тождество
Свойства логарифмов
(![]() )
)
![]()
Теорема косинусов
![]()
Тригонометрия
Простейшие
соотношения (![]() ):
):
![]() .
.
Основные тригонометрические формулы
![]() ,
,
![]()
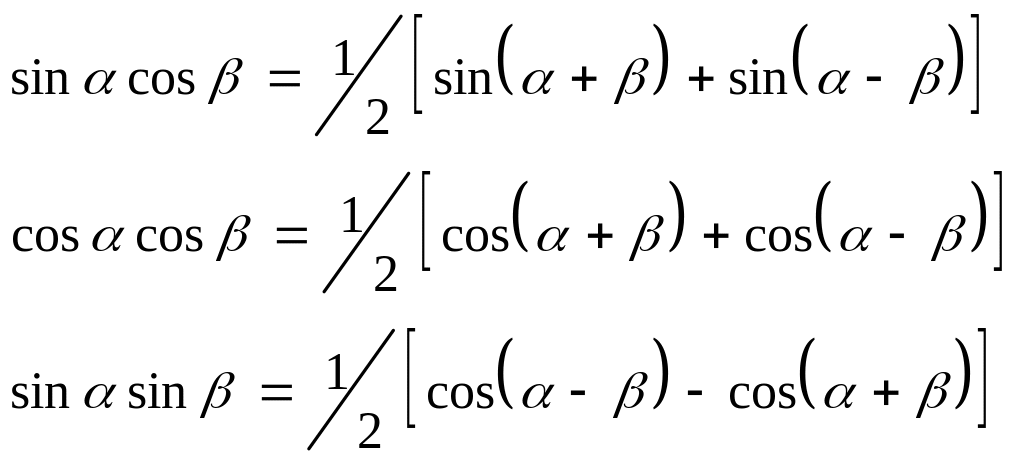
![]()
Знаки тригонометрических функций
Угол |
|
|
|
|
|
+ |
+ |
- |
- |
|
+ |
- |
- |
+ |
|
+ |
- |
+ |
- |
|
+ |
- |
+ |
- |
Некоторые значения
Угол |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
1 |
|
|
|
0 |
- |
- |
- |
-1 |
|
0 |
|
1 |
|
∞ |
- |
-1 |
- |
0 |
|
∞ |
|
1 |
|
0 |
- |
-1 |
- |
∞ |
Приложение 2
ТАБЛИЦА ИНТЕГРАЛОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТАБЛИЦА ПРОИЗВОДНЫХ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
Вид правой части f(x) |
Корни характеристического уравнения |
Вид частного решения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 3
Метод выбора частного решения
