16. Решение стохастического дифференциального уравнения – марковский процесс.

17. Диффузионноые процессы как решения стохастических уравнений.

(16) и (17) билеты – это одна и таже теорема – смотри доказательство. Половина док-ва о том, что решение является марковским процессом, а потом проверяются условия диффузионности.

Теорема: пусть (t) – решение стохастического дифференциального уравнения

где и , , - удовлетворяет условиям теоремы о  и 

Тогда (t) – является диффузионным процессом с перех. вер-тью:

При любых фиксированных , :

18. Однородные диффузионные процессы.

ОПР: пусть коэффициенты , в стохастическом уравнении не зависят от времени t

= , =

,

Тогда процесс (t) называется однородным.

Теорема: переходная вероятность однородного диффузион. процесса зависит только от (t - s)

19. Вероятностное решение задачи Коши для параболического уравнения.

Пусть - однородный диффузионный процесс, который является решением стохастического дифференциального уравнения: ,

Теорема: пусть функция является решением следующей задачи Коши

t  0, x 

(классическое уравнение теплопроводности)

где - равномерно ограниченно,

Тогда 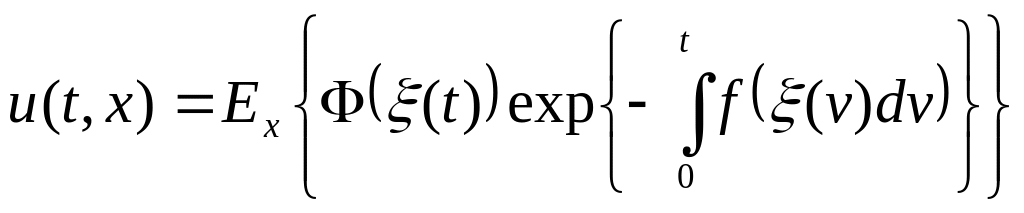, где

20. Вероятностное решение задачи Дирихле.

Теорема: пусть , - является решением задачи Дирихле

Тогда справедливо следующее вероятностное представление:

, где

Н – момент первого выхода диффузии из интервала.

21. Формула Фейнмана-Каца.

Этот билет идет в конспекте после билета (22). Вообще, надо поставить общую задачу Коши и разобраться с распределениями Лапласа...

Теорема:

Пусть - непрерывные функции, , - ограничена 

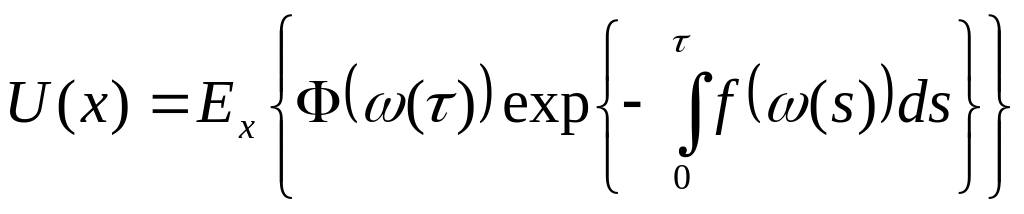
является единственным ограниченным решением диф.уравнения второго порядка

где  - экспоненциально распределенный момент остановки, не зависящий от бр. движения .

ОПР: функция называется кусочно-непрерывной, если  конечное число разрывов I рода.

(Разрыв I рода - это наиболее простой разрыв непрерывности функции, при котором -ют конечные определенные пределы как слева , так и справа . Значение функции в самой точке будет, вообще говоря, отличным от и )

Теорема:

- кусочно-непрерывные функции, , - ограничена 

является единственным ограниченным решением диф.уравнения второго порядка

Замечание: Уравнение с кусочно-непрерывными коэффициентами следует понимать как обычное уравнение во всех точках непрерывности, а в точках разрыва решение полагается непрерывным вместе с первой производной.

22. Распределения интегральных функционалов от броуновского процесса.

ОПР: Пусть - процесс броуновск. движения, и - обе непрерывные функции 

процесс

называется интегральным функционалом от процесса броуновского движения.

Ф.р. : ,

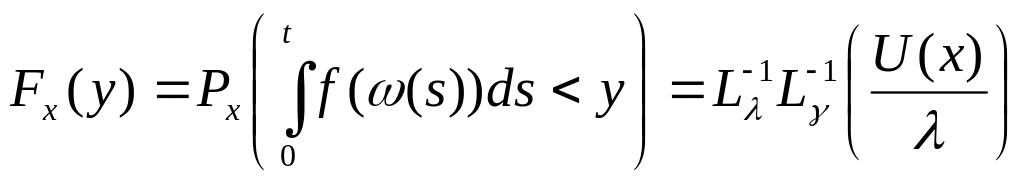23. Совместные распределения интегральных функционалов и инфиума и супремума броун. процесса.

Теорема: пусть - кусочно-непрерывные функции, 

является единственным ограниченным решением следующей задачи

,

- граничные условия

Замечание:

1. пусть - условие достоверно – можно убрать, U ограничено на -

2. пусть - условие достоверно – можно убрать, U ограничено на +

24. Условные распределения функционалов при условии, что конец траектории фиксирован.

Теорема: - кусочно-непрерывные неотрицательная функция  функция

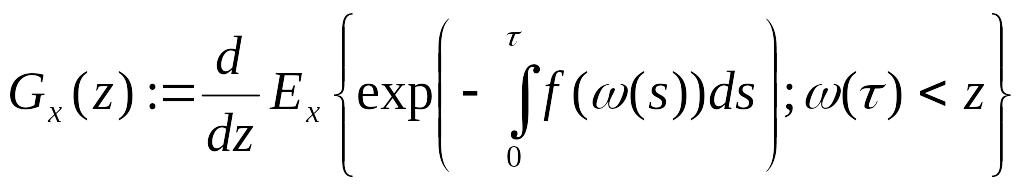
является единственным непр. ограниченным решением задачи

, (*)

а в точке x – скачек производной:

(*) – однородное дифференциальное уравнение, которое выполняется везде, кроме точки x.

25. Распределения функционалов от отраженного броуновского движения.

ОПР: Отражение броуновского движения является

Теорема: пусть - кусочно-непрерывные функции,  функция

(где  - экспоненциально распределенный момент времени с параметром , не зависящий от броуновского движения (t) и  от )

является единственным непрерывным решением следующей задачи

26. Распределения функционалов от броун. дв-я, остановленного в момент выхода на границу интервала.

Вспомним вероятностное решение задачи Дирихле (повтор):

Теорема: пусть , - является решением задачи Дирихле

Тогда справедливо следующее вероятностное представление:

, где

Сформулируем частные следствия этой теоремы (сам билет):

Следствие 1: пусть тогда получим следующую теорему

Теорема 1: пусть - кусочно-непрерывная функция,  функция

, где

единственное решение задачи

Следствие 2: пусть - индикаторная функция, получим теорему:

Теорема 2: пусть - кусочно-непрерывная функция,  функция

единнственное непрерывное решение задачи

Следствие 3: пусть - индикаторная функция, получим теорему:

Теорема 3: пусть - кусочно-непрерывная функция,  функция

единнственное непрерывное решение задачи

По Б.З. Вулих

Основные свойства пространства

Пространство - единственное из пространств , кторое оказывается гильбертовым.

ОПР: пусть означает совокупность всех вещественных измеримых функций , заданных и суммируемых с квадратом на отрезке :

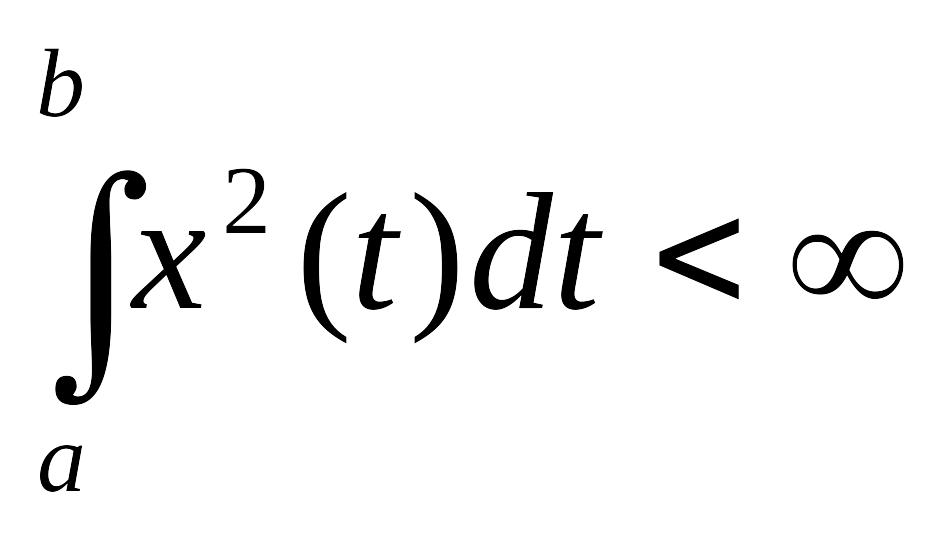
т.е. функция должна быть суммируемой. Эквивалентные функции отождествляются. Ясно, что в входят, в частности, все ограниченные измеримые функции, заданные на , тем более входят все непрерывные функции.

а) Проверим, что множество - линейная система:

- замкнута относительно опреаций умножения на const и сложения двух элементов из .

- произведение, будучи всегда суммируемым, может не входить в

б) Введем норму в по формуле: 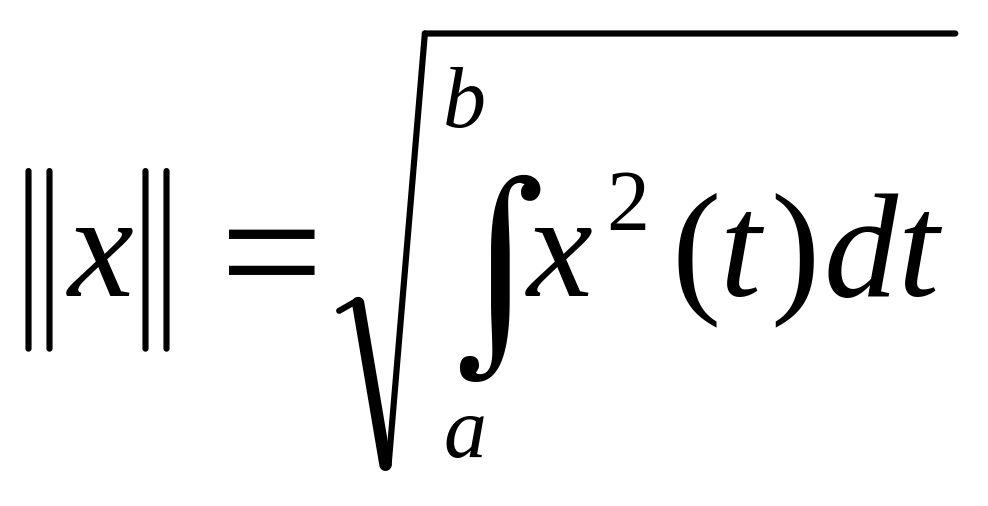- т.о. - нормированное пр-во

в) Пространство также банахово, и притом сепарабельное

г) В можно определить скалярное произведение так, что оказывается гильбертовым пространством. С этой целью для любых x,y  положим скалярное произведение (x,y) равным интегралу от произведения этих функций по всему интервалу :

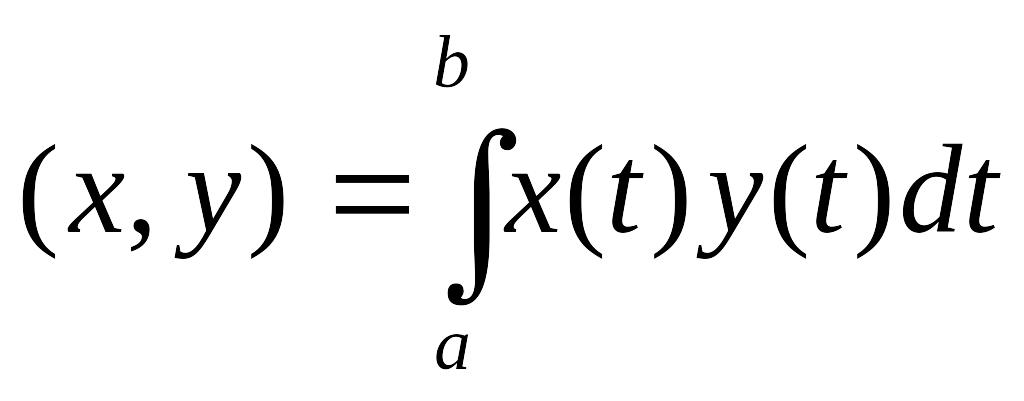
этот интеграл имеет конечное значение для любых x,y  . Ясно, что норма и скалярное произведение в связаны соотношением: . Следовательно, что поскольку пространство полно и сепарабельно, оно является сепарабельным гильбертовым пространством. Кроме того, оно бесконечно-мерно.

Можно рассматривать аналогичное пространство, составленное из функций, суммируемых с квадратом и допускающих комплексные значения. Скалярное произведение вводится:

ОПР: метрическое пространство называется полным, если в нем всякая фундаментальная последовательность имеет предел.

ОПР: последовательность точек метрического прост-ва называется фундаментальной (или сходящейся в себе), если при .

Теорема: если последовательность сходится к пределу, то она фундаментальна.

Теорема: всякая фундаментальная последовательность ограничена.

Пространства при любом полны. В терминах сходимости в среднем это значит, что если последовательность функций из сходится в себе в среднем р-того порядка, т.е. если при , то  функция из , к которой данная послед-ть сходится (тоже в среднем р-того порядка).

ОПР: Мн-во А точек метрического пр-ва Е называется всюду плотным (в Е), если .

ОПР: Метрическое пр-во называется сепарабельным, если в нем  счетное или конечное всюду плотное подмножество.

ОПР: Мн-во А точек метрического пр-ва Е называется компактным, если из  бесконечной посл-ти можно выделить частичную посл-ть ( ), сходящуюся в Е к некоторому пределу.

Теорема: Компактное пространство сепарабельно.

По Колмогоров-Фомин.

Напомним, что скалярным произведением в действительном линейном пр-ве R называется действительная функция , определенная для каждой пары элементов и удовлетворяющая следующим условиям:

1)

2)

3)

4) причем только при

ОПР: линейное пространство с фиксированным в нем скалярным произведением называется евклидовым пространством.

В евклидовом пространстве R вводится норма с помощью: .

Отметим, что в евклидовом пр-ве сумма, произведение на число и скалярное произведение непрерывны, т.е. если , (в смысле сходимости по норме), (как числовая последовательность), то

Доказательство этих фактов основано на неравенстве Коши-Буняковского:

Теорема Фату: Если посл-ть измеримых неотрицательных функций сходится почти всюду на А к f и , то f интегрируема на А и

Теорема Фубини: Пусть меры и определены на -алгебрах, -аддитивны и полны; пусть, далее:  =  и функция интегрируема по мере  на множестве 

Теорема Радон-Никодим: Пусть  некоторая конечная -аддитивная мера, определенная на -алгебре  подмножеств из Х, а Ф – заряд, определенный на той же -алгебре и абсолютно непрерывный относительно . Тогда  такая суммируемая по  функция f на Х, что

для каждого измеримого А. Эта функция, называемая производной заряда Ф по мере , определяется однозначно, с точностью до -эквивалентности (две функции называются -эквивалентными, если они совпадают почти всюду относительно меры ).

Теорема Лебега (о предельном переходе):

Если посл-ть на А сходится к f и при всех n , где  интегрируема на А,

то предельная функция f интегрируема на А и

ОПР: Простая (измеримая + не более, чем счетное число значений) функция f называется интегрируемой или суммируемой (по мере ) на мн-ве А, если ряд , где абсолютно сходится. Если f интегрируема, то сумма ряда называется интегралом от f по множеству А.

15