8. Тождества Вальда.

Теорема (1-ое тождество Вальда):

Пусть - последовательность нез.о.р. СВ,

- поток -алгебр, порожденный СВ , i = 1,2,…,k

 - момент остановки относительно :   

Тогда (верхн. индекс суммирования случайный – это момент остановки)

Теорема (2-ое тождество Вальда):

Пусть - последовательность нез.о.р. СВ,

- поток -алгебр, порожденный СВ , i = 1,2,…,k

 - момент остановки относительно :   

Тогда

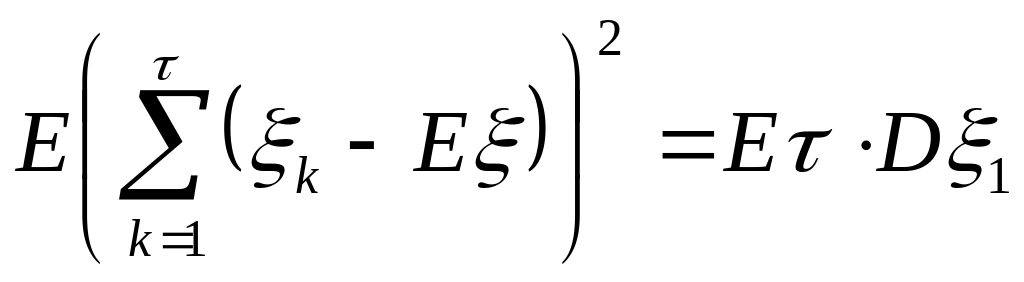
Теорема (фундаментальное тождество Вальда):

Пусть - последовательность нез.о.р. СВ, - хар. функция

- частичная сумма

 - момент остановки относительно

Тогда

9. Т-ма о числе пересечений субмартингалом полосы (a,b). Теорема (Дуба) о сходимости субмартингалов.

Интервал [a,b] рассмотренный во времени

Последовательность , k = 1,2,…, где = 0, а - -измеримо

Есть дискретные моменты времени, определим моменты остановки: пусть , а

- до пересечения уровня «a»

- после пересечения уровня «b»

Определим величину:

Пара моментов с нечетн. и четн. индексом называется пересечением полосы (a,b), а - число пересечений снизу вверх полосы (a,b) последовательностью до момента времени n.

Теорема (Т. Дуба о числе пересечений): пусть - субмартингал отн-но потока 

, где , - превышение уровня «a»

Теорема (Т. Дуба о сходимости субмартингалов):

пусть ( , ) – субмартингал,  п.н. (с вер. 1) и

Следствия:

1. пусть  0 – неположительный субмартингал сходится с вер-тью 1

2. пусть  0 – нетрицательный мартингал сходится с вер-тью 1

Лемма Бореля-Кантелли:

Пусть , k = 1,2,… - последовательность событий: ряд

Тогда с вер-тью 1  : n  наступает

10. Определение и свойства стохастического интеграла.

Броуновское движение: , пусть

Процесс с нез. приращениями: ,

1)

2)

Пусть  поток -алгебры : t - -измеримо

Независимость приращений вперед: для  - - не зависим от

Опишем класс подынтегральных функций, для которых Ито строил интегралы:

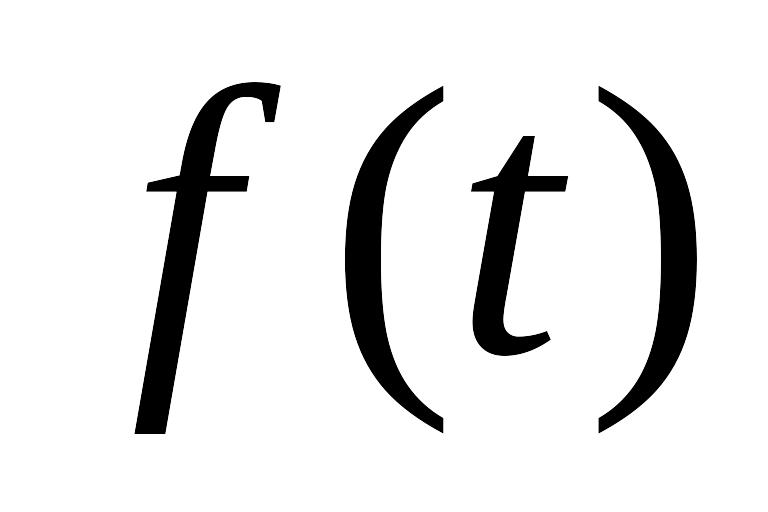1. , - -измерим (т.е. согласованность с потоком)

2. 

Речь идет о пространствах - квадрат нормы по мере произведения (вероятностная мера  мера Лебега).

Интеграл должен отвечать требованиям:

1. линейность:

2. 

3. 1.

2. 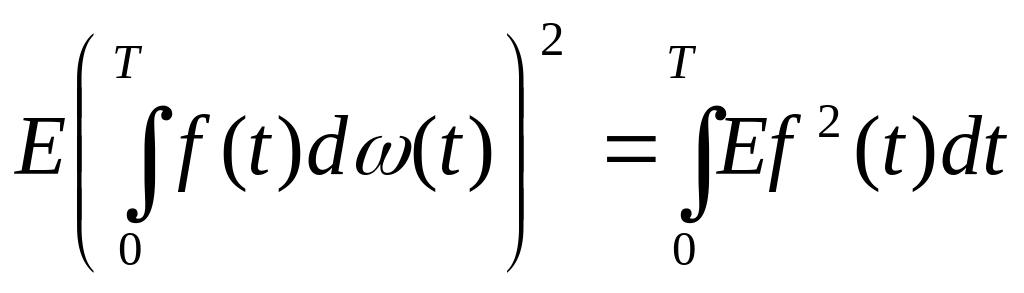- изометрия, совпадение норм

Разобъем [0,T] на интервалы: и определим ступенчатые функции:

- при этом - -измерима

Будем аппроксимировать только в левом конце.

ОПР: Стохастический интеграл для ступенч. функций:

Лемма: для f   последовательность ступ.функций  :

т.е.  последовательность ступ.функций, которые аппроксимируют f.

Для  аппр.посл-ти предел будет один и тот же. Этот предел I(Т) называется стохастическим интегралом подынтегральной функции  :

11. Свойства стохастического интеграла как функции верхнего предела.

Теорема:   процесс является непрерывным с вер-тью 1 и для  уровня   0 выполняется

Док-во: сначала для ступенчатых функций, а потом – для произвольных (!!!)