1. Определение случайного процесса (сп). Эквивалентность случайных процессов.

ОПР: СВ  - называется измеримое отображение:  F  ( , B ), где

B - борелевская -алгебра на евклидовом пр-ве , d = 1.

ОПР: СП называется семейство СВ, зависящее от параметрического множества Т: {(t), tT}

ОПР: СП – функция 2-х переменных (t, ). Функция (t, ), как функция от t при  фикс. 

(, ) или называется траекторией или реализацией СП.

Мн-во исходов  удобно трактовать как набор реализаций, т.о.  выступает как пр-во ф-ций.

ОПР: СП (t), Т = [a,b] называется измеримым, если (t, ) : явл-ся измеримым относительно -алгебры, порождаемой борелевскими множествами и -алгеброй F: (B F)

ОПР: -алгебра, порожденная процессом, - это наименьшая -алгебра цилиндрических мн-в:

ОПР: Случайные процессы (t) и (t) называются стохастически эквивалентными или эквивалентными в узком смысле, если они определены на одном параметрическом мн-ве Т и одном вероятностном пространстве (,F, Р) и

 tT Р((t) = (t)) = 1, где (t), (t) – одномерные величины при фикс. t

ОПР: Два стохастически эквивалентных процесса называются модификациями друг друга.

С каждым процессом связан набор конечномерных распределений (КМР), который задается:

 набора  B

- n-мерное распределение.

При изменении параметра из Т и из B будем иметь совокупность – она и есть набор КМР.

ОПР: Два СП, заданных на одном и том же параметрическом множестве, называются эквивалентными в широком смысле (слабом смысле), если у них совпадают наборы КМР.

УТВ: Эквивалентность в узком смысле  эквивалентность в широком смысле.

2. Основные классы случайных процессов.

1. Процессы с независимыми приращениями

ОПР: Процесс (t) называется процессом с независимыми приращениями, если для

 возрастающих моментов времени СВ приращения:

- являются нез.

Примеры: пуассоновский и броуновский процессы

2. Марковские процессы

ОПР: -алгеброй прошлого к моменту времени t называется -алгебра: =

где (s), s  [0,T] - процесс

ОПР: -алгебра настоящего - -алгебра, порожденная СВ (t): ((t)) =

ОПР: -алгебра будущего - -алгебра: =

ОПР: СП (t) называется марковским, если для  настоящего момента времени t и

 множеств А  и В  : - условная независимость

прошлого от будущего (при условии настоящего)

3. Мартингалы

Свойства условного мат.ожидания (отн-но -алгебры А): ,  - А-изм., СА

1. линейность:

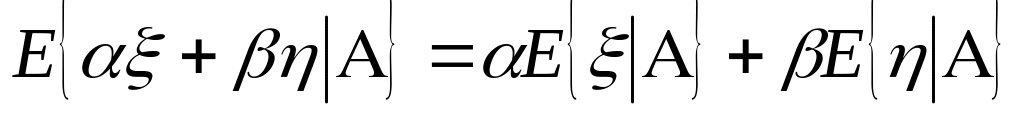
2. пусть  не зависит от А ( измеримая отн-но А – СВ  - не зависит от ):

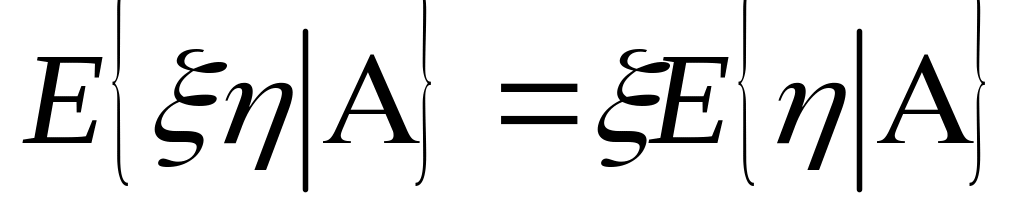
3. пусть ,  - СВ и  измеримо отн-но А:  при   1

4. есть две -алгебры M  A  F, (M - более бедная): E{M } = E{E{A}M }

(,F, Р), - возрастающий поток -алгебр, в любой момент времени s < t, s,t  T:

ОПР: (t), t  T называется мартингалом, если

1. конечность моментов + согласованность: t , процесс (t) - измерим

2. s < t, где s,t  T п.н. (с вер-тью 1) – усредняя значение процесса в будущем отн-но некоторой -алгебры прошлого, получаем значение процесса в прошлом.

ОПР: (t), t  T называется субмартингалом, если

1. конечность моментов + согласованность

2. s < t, где s,t  T п.н. (с вероятностью 1)

ОПР: (t), t  T называется супермартингалом, если

1. конечность моментов + согласованность

2. s < t, где s,t  T п.н. (с вероятностью 1)

Примеры: - мартингал – сумма н.о.р. СВ с 0-ым м/о,

- субмартингал – квадрат суммы н.о.р. СВ с 0-ым м/о

4. Гауссовские случайные процессы

ОПР: процесс (t), t  T называется гауссовским, если все его КМР есть гауссовские, т.е.

случайный вектор , - гауссовские

УТВ: процесс называется гауссовским, если линейные комбинации любых его наборов есть одномерные гауссовские величины.

УТВ: гауссовские величины выдерживают предельный переход: интеграл от гауссовского процесса – есть гауссовский процесс.

5. Стационарные случайные процессы

ОПР: процесс (t), t  T – стационарный в узком смысле, если его КМР не зависят от сдвига параметра, не выходящего за пределы параметрического множества, т.е:

и  t : + t  T  - не зависят от t.

Характеристики СП:

1. независимость от сдвига (МО не зависит от времени): - const

2. функция ковариаций зависит только отразности: R(s,t) = R(t-s)

ОПР: процесс (t), t  T – стационарный в широком смысле, если

1. t  T - конечны дисперсии

2. выполнены (1) и (2) выше (см. характеристики СП)