6. Микропроцессорный анализатор, работающий по алгоритму бпф

Краткие сведения о быстром преобразовании Фурье. Как уже отмечалось в § 7.2, БПФ — это алгоритм ускоренного выполнения ДПФ. При тех же результатах БПФ значительно сокращает чис­ло операций, требуемых для вычислений согласно (7.8) и (7.9). В результате применения БПФ в анализаторах спектра и других устройствах цифровой обработки сигналов увеличивается быст­родействие аппаратуры и сокращается необходимый объем па­мяти.

Известно несколько алгоритмов БПФ. Вид алгоритма зависит от выбора числа N. Наиболее простой и распространенный алго­ритм получается, когда , где п — целое число. Обычно число N настолько велико, что гарантируется выполнение выте­кающего из теоремы отсчетов (теоремы Котельникова) условия

(В— ширина спектра сигнала х(t) выраженная в гер­цах, а L— длительность сигнала, выраженная в секундах).

Кратко поясним сущность алгоритма БПФ [34] в той мере, которая представляется необходимой для пояснения принципа ра­боты рассматриваемого анализатора. Представим выражение (7.8) для прямого ДПФ в такой форме:

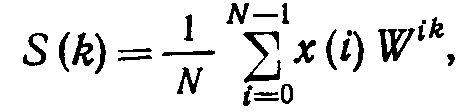
где

Так как число N выборок, осуществляемых при дискретиза­ции сигнала х(t), четное, то последовательность х(i) можно раз­бить на две последовательности, соответствующие четным и нечет­ным номерам выборок¹; где i=0, 1, 2, ..., . Каждая последовательность содержит N/2 членов. Например, при получаются такие последовательности:

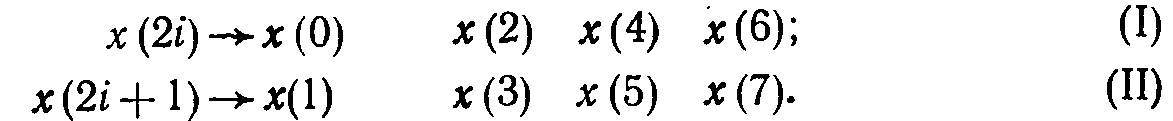
Применим дискретное преобразование Фурье к обеим последова­тельностям с учетом того, что они содержат по N/2 членов. Согласно (7.8) формула ДПФ для последовательности (I)

(7.29)

а для последовательности (II)

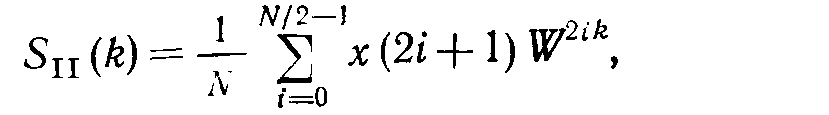(7.30)

где

Цель решаемой задачи — найти значения S(k) исходной по­следовательности . Поскольку члены обеих образованных из нее последовательностей относятся к последова­тельности х(i), то для S(k) справедливо выражение

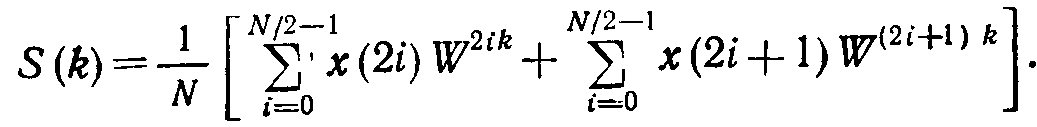(7.31)

Его можно переписать в форме

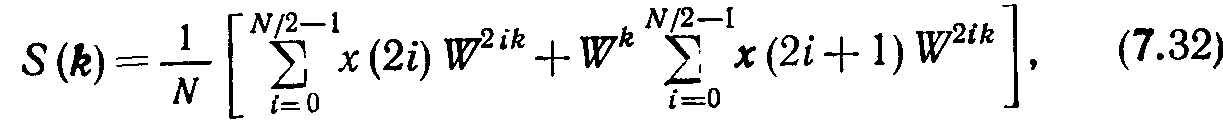
Где или

Для чисел k, отвечающих условию , коэффициенты принимают через период N/2 те же значения, что и при С учетом соотношения

соответствующая формула запишется в виде

(7.34)

Объединив (7.33) и (7.34), имеем

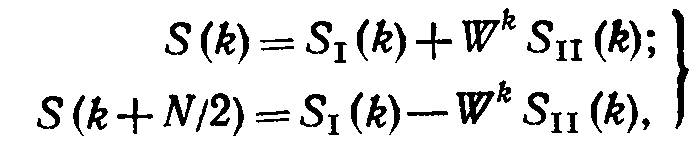(7.35)

где

Например, при N = 8, для k = 2

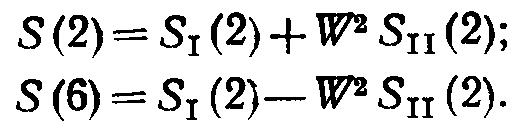
Полученные выражения показывают возможность определе­ния значений коэффициентов S(k) последовательности x(i), со­стоящей из N выборок, через значения коэффициентов ДПФ по­следовательностей , в каждой из которых содер­жатся по N/2 выборок. При этом для нахождения значений коэф­фициентов используются одни и те же значе­ния коэффициентов и произведения . Та­ким образом, требуется N операций сложения и N/2 операций умножения на W^k.

Продолжая аналогичные рассуждения, несложно свести вычи­сления значений коэффициентов ДПФ последовательностей (I) и (II), т. е. х(2i) и x(2i+l) к вычислению значений коэффициен­тов ДПФ четырех последовательностей по N/4 выборок в каж­дой.

Для приведенного примера (N = 8) из последовательности х(2i) образуются две последовательности:

а последовательность x(2i+1) соответственно распадается на такие последовательности:

В общем случае при N = 2ⁿ выборках возможны п шагов пос­ледовательного понижения порядка ДПФ. Так как на каждом ша­ге требуются N операций сложения и N/2 операций умножения, а число шагов , то для выполнения БПФ достаточно провес­ти операций сложения и операций умноже­ния.

Общее количество вычислительных операций составляет Сопоставление этого числа с числом 2N² операций, требуемых при обычном ДПФ, показывает, что применение алго­ритма БПФ позволяет уменьшить количество вычислительных опе­раций в раз. Так, если , то объем вычис­лений сокращается более чем в 100 раз.

Структурная схема анализатора. Обычно в приборах, работа­ющих по алгоритму БПФ, число дискретных выборок устанавли­вают (п—целое). Если n=10, т. е. N=1024, то БПФ заклю­чается в преобразовании в частотную область 1024 значений ди­скретных выборок (группы выборок) процесса, представленного во временной области. В результате прямого преобразования в частотной области получаются N комплексных значений, распо­ложенных на оси частот через интервал (где Т₀ — интер­вал дискретных выборок во временной области). Для упрощения преобразования рассматривают «физические» спектры, охватыва­ющие только область положительных значений частоты.

Число р эквивалентных фильтров, синтезируемых в результа­те БПФ, достаточно велико. Так, при группах выборок N—1024 число р достигает 400. Фильтр занимает частотный интервал Полоса пропускания (значения граничных частот на 3 дБ ниже значения средней частоты полосы) составляет: 0,88β— при линейной коррекции и 1,44β—при коррекции в виде «окна» Хеннинга.

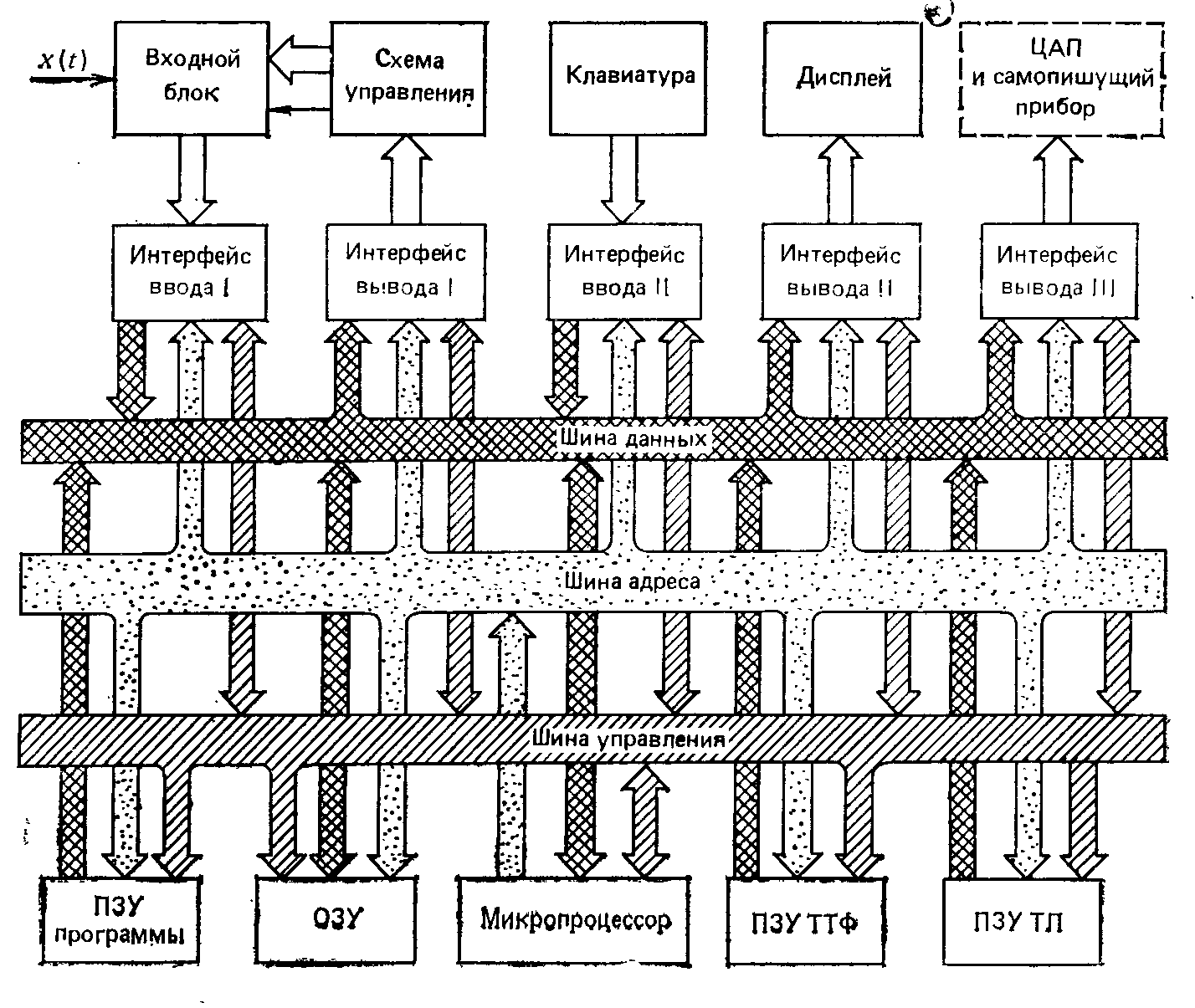
На рис. 7.16 приведена структурная схема анализатора спект­ра, содержащего микропроцессорную систему, с помощью кото­рой осуществляются вычисления по алгоритму БПФ, решаются за­дачи управления вводом информации, опроса клавиатуры, ото­бражения результатов анализа дисплеем, усреднения спектров и др.

Микропроцессор выполняет вычисления согласно программе, хранимой в ПЗУ программы. При этом дешифратор кода опера­ции дешифрирует не только команды, содержащиеся в програм­ме, но и информацию о положении органов управления клавиату­ры, определяющую подпрограммы. Полученные сигналы служат для управления работой системы. Чтобы ускорить вычислительную процедуру, в составе микропроцессорной системы предусмот­рено ПЗУ, в котором содержится таблица тригонометрических функций (ПЗУ ТТФ). Она используется также при вычислениях, проводимых для коррекции, соответствующей «окну» Хеннинга. Эта процедура выполняется по отношению к группе значений ди­скретных выборок, полученных во временной области, т. е. еще до преобразования в частотную область. Имеющееся в составе мик­ропроцессорной системы ПЗУ, содержащее таблицу логарифмов (ПЗУ ТЛ), облегчает и ускоряет переход от линейного масштаба к логарифмическому.

Для хранения данных, используемых в процессе вычислений, служит ОЗУ. От его емкости зависят возможности анализатора. Например, в одном из анализаторов, работающем в диапазоне частот от 0,025 Гц до 20 кГц, емкость ОЗУ составляет 8 Кбайт (4096 двухбайтовых слов).

Прибор снабжен интерфейсной картой (на рис. 7.16 ИКАР не показана), связанной с микропроцессорной системой. Это позво­ляет подключать анализатор к интерфейсной шине (см. § 12.4).

Хотя БПФ и ускоряет решение задачи, все же для его осу­ществления требуется большое число вычислительных операций. Так, чтобы преобразовать одну группу N= 2¹⁰ выборок, необходи­мо около 10 000 операций. Особенно продолжительны операции пе­ремножения чисел. Поэтому расширение частотного диапазона исследуемых сигналов связано с ускорением перемножительных операций. Для этого в схему анализатора вводят специализиро­ванные микропроцессоры — матричные перемножители, а также применяют 16-разрядные универсальные микропроцессоры, архи­тектура которых предопределяет возможность аппаратного пере­множения чисел. В последние годы выпускаются БИС специали­зированных микропроцессоров, выполняющие БПФ (прямое и об­ратное) .

Входной блок. Возможности рассматриваемого анализатора спектра в значительной мере определяет входной блок, управля­емый микропроцессорной системой. Его структурная схема в сочетании со схемой управления изображена на рис. 7.17.

Как видно из рис. 7.16 и 7.17, схема управления, получающая команды микропроцессорной системы через интерфейс вывода I,

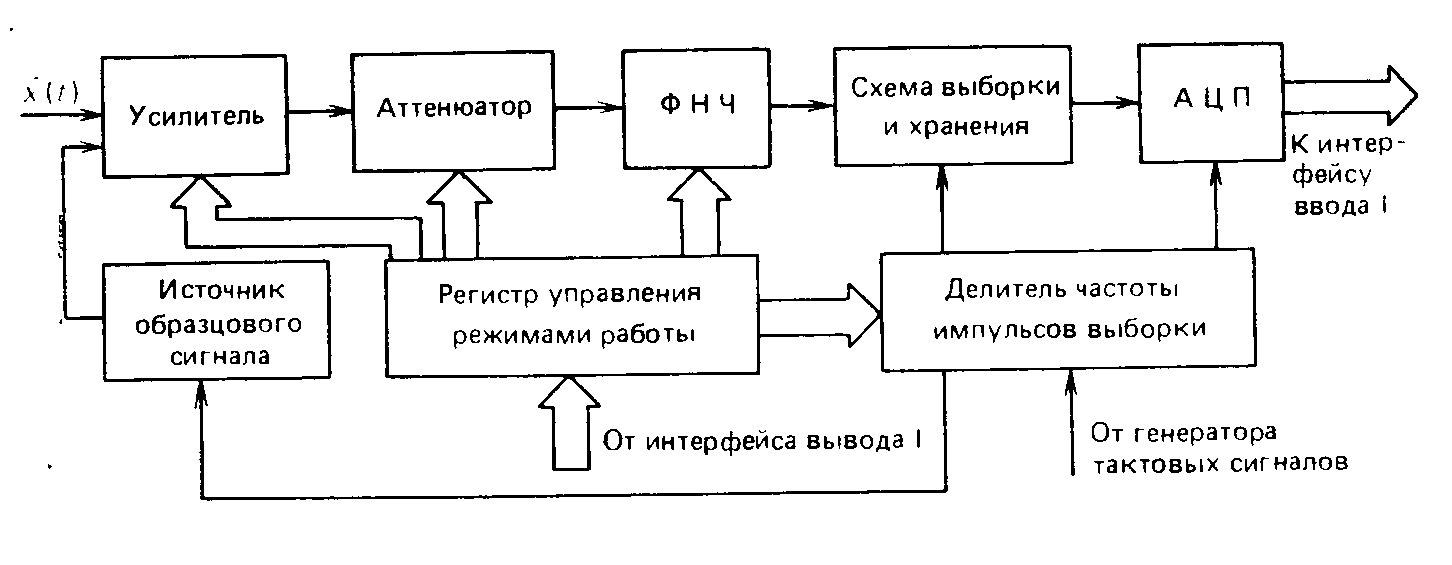
автоматически регулирует коэффициент усиления усилителя и коэффициент передачи аттенюатора. ФНЧ, служащим для «отсеч­ки» составляющих, частоты которых выше верхней границы F_в установленного частотного поддиапазона анализа, также управ­ляет микропроцессорная система. Управление заключается в ав­томатической перестройке частоты среза фильтра: он настраи­вается так, что при любом установленном поддиапазоне частот. Возможно и дистанционное управление ФНЧ через интер­фейс.

С выхода ФНЧ анализируемый сигнал поступает на схему вы­борки и хранения, осуществляющую дискретные выборки в соот­ветствии с подаваемыми на ее управляющий вход тактовыми им­пульсами-выборками. Частота следования этих импульсов при пе­реключении частотных поддиапазонов автоматически (с помощью делителя частоты) устанавливается равной . Запомненные на короткий интервал значения исследуемого сигнала, получен­ные при дискретных выборках, преобразуются АЦП в числовые эквиваленты. Они передаются через интерфейс ввода 1 на шину данных микропроцессорной системы, осуществляющей обработку информации согласно алгоритму БПФ.

В составе входного блока содержится источник образцового сигнала, служащий для калибровки параметров усилителя и ат­тенюатора, а также других узлов. Частота образцового сигнала автоматически выбирается так, чтобы ее значение соответствова­ло определенному номеру светящейся полоски, наблюдаемой на экране дисплея.

Дисплей. На рис. 7.18 приведена структурная схема дисплея анализатора. Информация, которая должна быть отображена ЭЛТ, выдается из микропроцессорной системы через интерфейс вывода II в цифровую память. Поступление конкретных данных в память определяется нажатыми клавишами, которые входят в состав клавиатуры, расположенной на передней панели прибора. В памяти могут храниться числа, полученные при дискретных выборках с помощью АЦП, данные, относящиеся к мгновенному спектру, данные, характеризующие усредненный спектр. Все они могут поочередно отображаться дисплеем. Информация вводится в цифровую память во время обратного хода луча ЭЛТ. Управле­ние программное, причем используется режим прерывания.

Дисплей может отображать большое число хранимых в памя­ти дискретных значений (например, р = 400). В случае, когда воз­никает необходимость вывода на экран значений дискретных вы­борок исследуемого сигнала, то из группы выборок (N=1024) отображается только часть их (k выборок), например каждая третья выборка (р' = 390). Предусмотрена возможность и отобра­жения выборок, следующих одна за другой, причем отображае­мый участок можно смещать по оси времени.

Размер изображения по вертикали соответствует широкому динамическому диапазону, выражаемому в логарифмических еди­ницах (например, 80 дБ). Нижнему и верхнему пределам диапа­зона соответствуют граничные линии масштабной сетки экрана. Значение верхнего предела устанавливается с помощью клавиш (80, 40 или 20 дБ)

Так как с помощью схемы управления узлами входного блока (рис. 7.17), можно изменять затухание аттенюато­ра ступенями через 10 дБ, то имеется возможность наблюдать как изображение спектра во всем динамическом диапазоне (80 дБ), так и расширенные по вертикали изображения частей спектра (40 или 20 дБ).

На экран ЭЛТ одновременно с отображаемой картиной с по­мощью генератора знаков выводится буквенно-цифровая инфор­мация об установленных пределах динамического и частотного поддиапазонов, числовых значениях и единицах измерения раз­личных параметров исследуемого сигнала, число отображаемых дискретных значений, число усредненных спектров, а также порядковый номер, значения частоты и уровня для выбранной (с помощью соответствующей клавиши) светящейся полоски в изо­бражении спектра. Если в схеме анализатора предусмотрены спе­циальные интерфейс вывода и ЦАП на рис. 7.16 они показаны

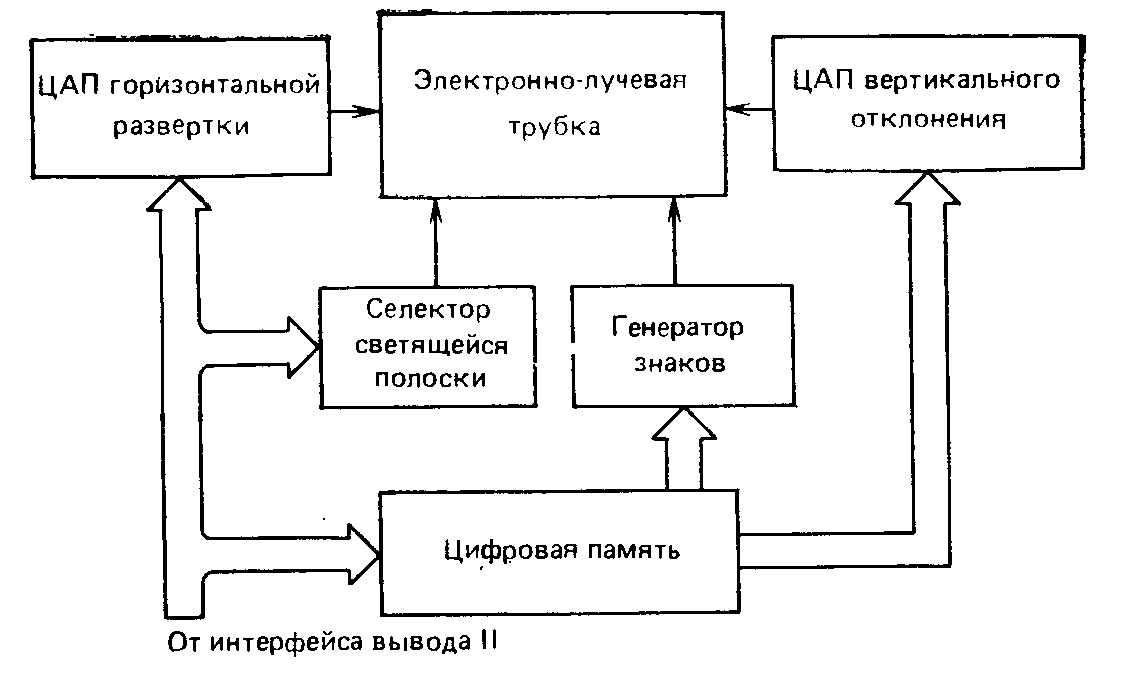
штриховыми линиями), то информация об отображаемом диспле­ем спектре может быть выведена на самопишущий прибор.

Программное управление. Как уже отмечалось, рабочая про­грамма, определяющая весь ход функционирования анализатора спектра, содержится в ПЗУ программы (рис. 7.16). Помимо ос­новной части она включает также ряд подпрограмм. Одна из них — подпрограмма прерывания при вводе исходной (аналоговой) ин­формации. Она управляет опросом клавиатуры и в соответствии с положениями клавиш процедурой запуска, формирования групп дискретных выборок и ввода данных.

Момент начала обработки группы значений выборок может совпадать с моментом запуска или задержки на определенное время (до 9,9 N). Как уже отмеча­лось, коррекция, соответствующая «окну» Хеннинга, может быть проведена еще во временной области. Ее выполнением управляет указанная подпрограмма. Другая программа прерывания использу­ется для вывода данных из ОЗУ в цифровую память дисплея (рис. 7.16 и 7.18).

Отдельные подпрограммы предусмотрены для усреднения спек­тров, число которых определяется соответствующими клавишами. Возможны алгоритмы линейного усреднения и экспоненциального сглаживания (см. § 8.5). Имеется также подпрограмма, позволяю­щая запоминать значения амплитуд спектральных составляющих или максимальных значений, соответствующих высотам светящихся полосок.