4. . Особенности спектрального анализа случайных

ПРОЦЕССОВ

Как уже отмечалось в § 7.2, спектральной характеристикой стационарного случайного процесса X(t) служит спектральная плотность мощности Gx(f). Она выражает среднюю мощность, вы­деляемую на резисторе сопротивлением в 1 Ом, которая прихо­дится на единицу полосы частот. Картину распределения средней мощности случайного процесса по частотам называют спектром мощности.

Аппаратурный анализ проводится одним из трех методов: фильтрации, определения спектральной плотности мощности по измеренной корреляционной функции в соответствии с теоремой Винера — Хинчина, вычисления спектральной плотности преобра­зованием Фурье реализации случайного процесса — по алгоритму быстрого преобразования Фурье (БПФ).

Для аппаратурного определения спектра требуется значитель­ное время. Нередко оно превышает длительность существования реализации или время, в течение которого сохраняется стационар­ность исследуемого процесса. Оценки спектра мощности, полу­ченные по одной реализации стационарного эргодического про­цесса, не всегда приемлемы. Поэтому приходится выполнять мно­гочисленные измерения, так как необходимо усреднять и по вре­мени, и по ансамблю.

Специфика метода фильтрации. Как следует из (7.17), сред­няя мощность Р_х стационарного случайного процесса X (t):

Если спектр сигнала ограничен частотами то средняя мощность в полосе ∆f (в окрестности часто­ты f )

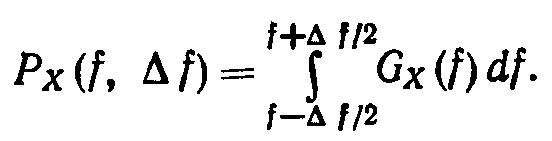
В случае, когда полоса частот конечна, но настолько узка, что спектральную плотность мощности Gx(f) можно полагать по­стоянной в этой полосе, получается приближенная формула

(7.24)

Из (7.24) видно, что спектральную плотность мощности мож­но определить, измерив среднюю мощность в известной узкой по­лосе. Следовательно, прибор для измерения спектральной плотно­сти мощности рассматриваемым методом (анализатор) должен содержать систему: полосовой фильтр с узкой полосой пропуска­ния — квадратор — усреднитель — дисплей (рис. 7.11). При измерениях обычно полагают, что спектральная плотность мощ­ности постоянна в полосе пропускания узкополосного фильтра.

Напряжение - длительность реализации или продолжитель- ность анализа), снимаемое с выхода усреднителя, со­ответствует оценке спектральной плотности мощности. При ана­лизе реализации эргодического стационарного процесса значения и(Т, Т), отсчитываемые в моменты t=T, флуктуируют около математического ожидания , причем

отклонения в среднем уменьшаются с увеличением продолжительности усреднения (по­стоянной времени сглаживающего фильтра).

Необходимо остановиться «а вопросе рационального выбора ширины полосы анализирующего (узкополосного) фильтра и про­должительности усреднения. Проводя аппаратурный анализ, сле­дует учитывать принцип неопределенности, который выражается соотношением¹ . Это означает, что сужение полосы требует соответствующего увеличения длительности измерения, причем уменьшение и увеличение Т в одинаковое число раз лишь сохраняют неизменной точность измерений.

При фиксированной продолжительности Т сужение полосы пропускания узкополосного анализирующего фильтра приводит к значительным флуктуациям оценки Gx(f) и статистическая на­дежность результатов будет низкой.

Интервал усреднения Т должен быть существенно больше ин­тервала корреляции узкополосного процесса (см. § 8.5). Так как то выполнение неравенства в слу­чае применения весьма узкополосного анализирующего фильтра приводит к увеличению интервала измерения и при усреднении с помощью ФНЧ требует установки последнего с еще более узкой полосой, что практически не всегда допустимо и выполнимо.

Статистическая погрешность измерения методом фильтрации. В соответствии с изложенным вначале, если среднее значение ста­ционарного случайного процесса X(t) равно нулю, то измерение спектральной плотности мощности сводится к измерению диспер­сии случайного процесса Y(t), получаемого на выходе узкополос­ного фильтра. Следовательно, статистическая погрешность изме­рения значения Gx{f) определяется соответствующей погрешно­стью измерения дисперсии D_y (§ 8.6).

Полагая, что процесс Y (t) характеризуется гауссовским рас­пределением вероятностей, можно записать формулы для относи­тельных среднеквадратических погрешностей измерений спект­ральной плотности мощности (усреднение идеальным интегра­тором) и (усреднение с помощью ФНЧ) [47]:

(7.25)

где d равно 1 для идеальных низкочастотных и радиофильтров, 1/2 для одиночного колебательного контура, для гауссов­ского радиофильтра; Т — продолжительность интегрирования: — эффективная шумовая полоса анализирующего фильтра; α — величина, обратная постоянной времени усредняющего ФНЧ.

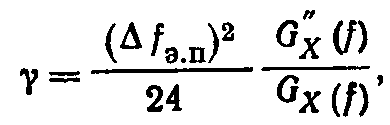
где — вторая производная по частоте спектральной плотности мощно­сти

Оптимальная (в смысле минимума суммарной среднеквадратической погреш­ности) полоса пропускания анализирующего фильтра:

при усреднении идеальным интегратором (длительность интервала Т фикси­рована)

при усреднении с помощью ФНЧ

Определение спектральной плотности мощности по корреляци­онной функции. Для действительных стационарных случайных функций согласно(7.16)

Соответственно оценка спектральной плотности мощности

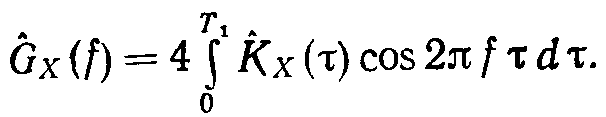(7.26)

Непосредственно измеряют корреляционную функцию, а значе­ние Gx(f) вычисляют по (7.26). Эту задачу решают корреломет­ры, дополненные устройствами для вычисления спектральной плотности мощности по значениям функции корреляции.

Оценка (7.26) оказывается неприемлемой в тех случаях, когда требуется выяснить тонкую структуру спектра мощности, так как «отсечение» участка кривой функции корреляции , соответ­ствующего значениям аргумента может привести к значи­тельным искажениям аппаратурного спектра в низкочастотной об­ласти.

Для получения подходящей оценки спектральной плотности мощности в (7.26) подынтегральное выражение умножают на ве­совую функцию , которую в литературе часто называют «ок­ном» («корреляционным окном»),

С учетом весовой функции выражение для оценки спек­тральной плотности мощности можно представить в виде

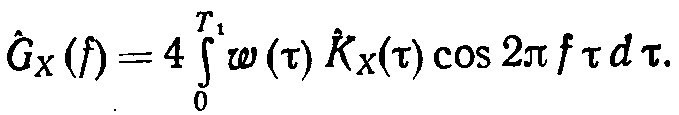(7.27)

Состоятельность оценки определяется выбранным «окном», т. е. видом функции . В (7.26) «прямоугольное окно»

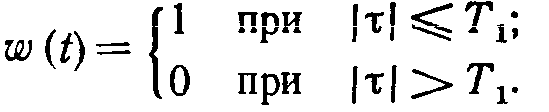(7.28)

Выбор «окна» зависит от характера исследуемого спектра мощности и от той конкретной задачи, ради решения которой про­водятся измерения [23, 47, 69, 109].