Измерения спектральных характеристик сигналов

1. Общие сведения

В предыдущих главах при измерении параметров электричес­ких сигналов (предполагалось представление их во временной об­ласти: значения сигналов рассматривались как функции времени. Для решения ряда задач целесообразно пользоваться представ­лением сигналов в частотной области, опираясь на зависимость значений или определенных параметров сигнала от частоты. Пред­ставление в частотной области иначе называют спектральным представлением. Как доказывается в теории сигналов, между обои­ми представлениями имеется полное соответствие: данной функ­ции во временной области всегда соответствует единственная функция в частотной области. Целесообразность выбора формы определяется характером и условиями решаемой задачи.

Характеристики, описывающие свойства сигнала при частот­ном представлении, называют спектральными. Наиболее полными характеристиками служат частотные спектры (амплитуд, мощнос­ти, фаз). Их математические определения содержатся в § 7.2. Для оценки степени 'нелинейных искажений, претерпеваемых синусо­идальным сигналом при прохождении через нелинейную цепь, ис­пользуют коэффициент гармоник. К спектральным характеристи­кам относятся кепстр, девиация частоты ЧМ сигнала и другие характеристики.

Здесь основное внимание уделяется аппаратурному спектраль­ному анализу, т. е. экспериментальному анализу, осуществляемо­му с помощью специальных приборов—анализаторов спектра. Поскольку современные анализаторы, как правило, позволяют ис­следовать спектры и детерминированных, и случайных сигналов, то в данной главе излагается спектральный анализ сигналов обоих видов (хотя измерению других характеристик случайных процес­сов посвящена отдельная глава —гл. 8).

Рассмотрению методов аппаратурного спектрального анализа и принципов построения анализаторов предпошлем основные ма­тематические определения спектров.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КЛАССИФИКАЦИЯ СПЕКТРОВ

Периодический сигнал, который описывается (функцией f(t), отвечающей условиям Дирихле, можно представить рядом Фурье

где) —постоянная составляющая, k—номер гармоники, — амплитуда гармоники, а и — ее частота и фаза соответственно.

Совокупность величин си называют спектром амплитуд, а сово­купность (величин ерь — спектром фаз. В настоящей .главе рассмат­ривается исследование спектра амплитуд (и спектра мощности), который в дальнейшем, как это принято їв литературе и радиотех­нической практике, мы будем называть просто «спектр».

Спектр периодического сигнала —линейчатый. Для непе­риодических сигналов характерен сплошной спектр. Функциональ­ное преобразование детерминированного сигнала х(t) из времен­ной области в частотную представляет прямое преобразование Фурье:

где — угловая частота.

Для преобразования из частотной области во (временную слу­жит обратное преобразование Фурье — интеграл Фурье:

(7.3)

Формулы (7.2) и (7.3), имеющие (симметричную структуру, на­зывают парой преобразований Фурье. Следует подчерк­нуть, что —комплексная функция, содержащая информацию и о спектре амплитуд, и спектре фаз. Эту функцию принято на­зывать комплексным спектром. Модуль функции —спектр амплитуд. Значение | | (выражает не непосредственную ампли­туду, а спектральную плотность.

Цифровые методы спектрального анализа опираются на дис­кретное преобразование Фурье. Кратко поясним еш сущность и приведем математические формулы.

При дискретизации времени непрерывный сигнал х(t) (преоб­разуется в последовательность дискретных выборок. Если вы­борки осуществляются регулярно через интервал (времени То, то получается последовательность , где i =0, 1, 2,…, N—1 (об­щая длительность ).

Полагают, что функция периодическая и ее период T=NT₀. Соответствующая ей функция в частотной области может быть представлена функцией дискретных значений часто­ты ( k= 0, 1, 2, ..., N—1), разделенных частотными интервалами . Обе функции и связаны парой дис­кретного преобразования Фурье (ДПФ): прямого

(7.4)

и обратного

(7.5)

причем

Поскольку функция рассматривается как периодичес­кая с периодом NT₀, то, когда функция преобразуется в функцию , получается один период сигнала x_n(iT₀). Под­разумевается, что он циклически повторяется. Функция , определяемая прямым дискретным преобразованием Фурье из , периодическая в частотной области с N значениями в каж­дом периоде (И только N/2 значений не повторяются.)

Таким образом, если функции x(t) и S(f) представляют пару непрерывного преобразования Фурье, описываемую (7.2) и (7.3), то последовательности

(7.6)

и

(7.7)

образованные выборками периодических функций¹, представляют пару ДПФ, удовлетворяющую (7.4) и (7.5). Ее записывают и в такой форме:

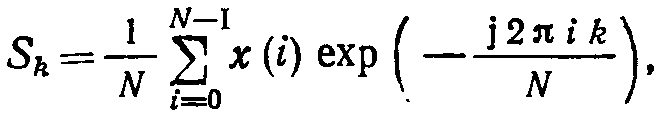(7.8)

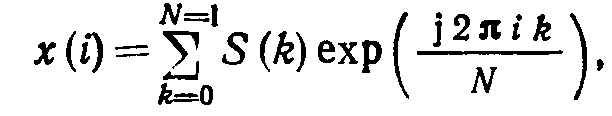(7.9)

где - i-я выборка последователь­ности (7.6), каждый период которой содержит N выборок.

Вычисления, проводимые при выполнении ДГТФ, довольно гро­моздки: они требуют примерно N² арифметических операций (на­пример, при N=1000 необходимы 1 000 000 операций). Для уско­рения преобразования разработан алгоритм (точнее, алгоритмы), значительно сокращающий объем и продолжительность вычисли­тельных операций. Его называют быстрым преобразова­нием Фурье (БГТФ). Процедура БПФ изложена во многих источниках, «апример в [3, 23, 34, 43, 69]. Краткие сведения о БПФ приведены в § 7.7.

К спектральным характеристикам, используемым на практике, относятся также текущий и мгновенный спектры. Как следует из (7.2), для нахождения спектра сигнала x(t) необходимо выпол­нить интегрирование по времени в бесконечных пределах. Но реальные физические процессы исследуются в течение конечного времени, и, следовательно, интегрирование ведется в пределах от момента начала наблюдения до данного, текущего (момента t). С учетом этого обстоятельства определяемый спектр может быть представлен в виде

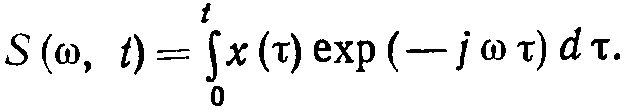(7.10)

Функция является функцией не только частоты, но и времени и носит название текущего спектра [99]. Это понятие важно для теории и техники анализа спектра. Дело в том, что периодичность процесса проявляется лишь за достаточно большое время — по крайней мере за несколько периодов. В течение же небольшой части периода характерные черты процесса вырисовы­ваться не успевают. Спектр короткого отрезка процесса—оплош­ной, так как этот отрезок по существу является коротким импуль­сом. Переход к линейчатому спектру (происходит лишь в пределе, когда (строго теоретически); на практике длительность про­цесса оказывается достаточной при условии .

Мгновенный спектр описывается функцией

(7.11)

и определяется как спектр отрезка сигнала длительностью Т, не­посредственно предшествующего данному моменту t [99].

Более общее определение мгновенного спектра записывается в виде

(7.12)

где —скользящая весовая функция.

Если записать (7.11) в виде

то мгновенный спектр нужно рассматривать мак разность двух текущих спектров, т. е. как приращение текущего спектра за ин­тервал времени Т. Это яриводит к определению мгновенного спек­тра по Пейджу

(7.13)

Где - текущий спектр.

Спектральной характеристикой стационарных случайных про­цессов (напряжения или тока) служит спектральная плотность мощности Она выражает приходящуюся «а единицу поло­сы частот 'среднюю мощность процесса (выделяемую на резисторе в 1 Ом). Соотношение между спектральной плотностью стационар­ного случайного процесса X(t) и его корреляционной функцией дается парой преобразований Фурье (теорема Винера— Хинчина):

(7.14)

(7.15)

В (7.14) и (7.15) спектральная плотность определена для по­ложительных и отрицательных значений частоты, причем . Помимо такого двустороннего «математического» спектра, при прикладных исследованиях и измерениях пользуются односторонней «физической» спектральной плотностью , отличной от нуля лишь при частотах . Для нее справедливы следующие формулы Винера—Хинчина:

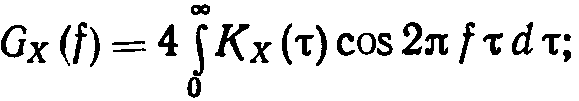(7.16)

(7.17)

Спектральную плотность мощности (спектр мощности) можно выразить через текущий спектр напряжения реализаций:

, (7.18)

где М — символ математического ожидания, а также через мгно­венный спектр .

(7.19)

При теоретических и практических исследованиях нередко пользуются нормированной спектральной плотностью стационар­ного случайного процесса

(7.20)

где - дисперсия случайного процесса

Функция связан а с нормированной корреляционной функ­цией выражением

(7.21)

Полезной характеристикой служит кепстр, представляющий собой обратное преобразование Фурье натурального логарифма нормированного спектра :

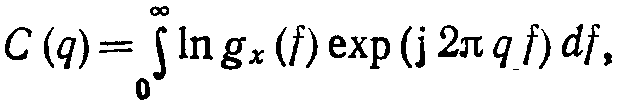(7.22)

где буквой q обозначена переменная, имеющая размерность вре­мени (она не идентична переменной )