4. Измерение частоты методом дискретного счета

Сущность метода. Данным методом проводят измерение сред­ней частоты периодического сигнала. Оно заключается в прямом сравнении значения измеряемой частоты с дискретным значени­ем Fобр образцовой частоты, воспроизводимым мерой в качестве единицы. Для этого находят (путем дискретного счета) число n, показывающее, во сколько раз больше .

Искомое значение частоты определяется выражением

и, следовательно, единица дискретизации равна -

Как указывалось в § 4.1, средняя (за интервал Δt) частота пе­риодического сигнала определяется как отношение числа п пери­одов сигнала к значению Δt. Следовательно, если выбрать интер­вал времени так, чтобы его значение , сосчитать число п периодов исследуемого сигнала за этот интервал и вычислить отношение , то найдем значение измеряемой частоты.

Сначала рассмотрим измерение частоты следования импульсов.

На рис. 4.15,а представлена исследуемая периодическая после­довательность импульсов, частоту следования F_х которой нужно измерить. Мера вырабатывает также периодическую последова­тельность импульсов с образцовой частотой следования F_обр (рис. 4.15,6).

Задача сравнения частот F_х и Fобр упрощается, если перейти к сравнению периодов Т_х и Тoбр. Так как то

.

Число n показывает, сколько периодов Т_х укладывается в ин­тервале Тобр.

Сформируем из двух соседних импульсов периодической после­довательности образцовой частоты, которые разделены интерва­лом времени Тобр, стробирующий импульс — временные ворота и обозначим их длительность Δtк (индекс «к» указывает, что интер­вал Δtк — калиброванный, образцовый). Очевидно, что Δtк =Toб_P. Заполним эти ворота импульсами, следующими с периодом Т_х (рис. 4.11,в). Число n импульсов, попадающих в ворота, длитель­ность ворот Δtк и период Т_х следования импульсов исследуемой последовательности связаны очевидным соотношением n= Δtк/T_x, из которого получается рабочая формула для определения час­тоты:

(4.12)

Таким образом, алгоритм измерения предписывает следующие операции:

сформировать стробирующий импульс — временные ворота, длительность которых равна периоду сигнала образцовой частоты:

Δtк=Тоб_Р;

заполнить временные ворота импульсами, следующими с иско­мой частотой F_х

сосчитать число п импульсов, попадающих в ворота;

вычислить отношение n/ Δtк.

Теперь перейдем к измерению частоты f_х непрерывного перио­дического сигнала, например синусоидального (рис. 4.16,а). Опираясь

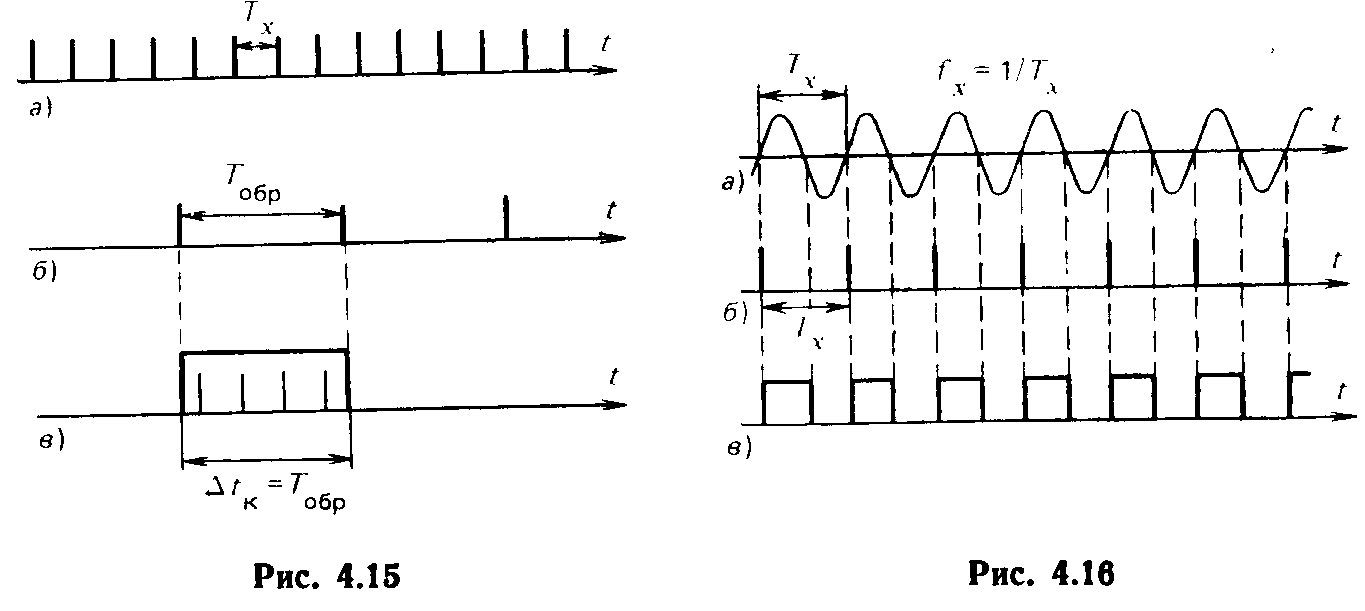
на изложенное, можно утверждать, что для выполнения та­кого измерения достаточно преобразовать исследуемый сигнал в периодическую последовательность либо коротких импульсов, мо­менты появления которых соответствуют моментам перехода си­нусоидального сигнала через нулевой уровень с производной од­ного и того же знака (рис. 4.16,6), либо в периодическую последовательность импульсов, соответствующих положительным полупериодам исходного сигнала (рис. 4.16,в). В результате преобразо­вания получается периодическая последовательность импульсов с периодом следования, равным периоду исследуемого сигнала, и таким образом задача сводится к уже рассмотренному измерению периода следования импульсов. Искомая частота находится из формулы, аналогичной (4.12):

(4.13)

Это среднее значение частоты за интервал Δtк.

Измерения оказываются косвенными. Чтобы получались прямые показания, в частотомерах, построенных по схеме с жесткой логи­кой, т. е. без микропроцессора, устанавливают длительности вре­менных ворот (на лицевой па­нели прибора переключатель длительности ворот обозначен над­писью ВРЕМЯ ИЗМЕРЕНИЯ). Когда р = О, т. е. Δt=1 с, то f_х=п в герцах.

Структурная схема частотомера. Современные цифровые час­тотомеры, даже выполненные по схемам с жесткой логикой, — приборы многофункциональные (но переход от одной функции к другой осуществляется посредством электромеханических комму­таторов), работающие в нескольких режимах: измерения часто­ты синусоидального сигнала, частоты следования импульсов, пе­риодов этих сигналов, длительности импульса, интервалов вре­мени, заданных двумя импульсами (одного или разных источни­ков), вариации частоты, отношения двух частот, прямого счета импульсов, счета числа N импульсов с предварительной установ­кой числа N и др. Поэтому следует иметь в виду, что изображен­ная на рис. 4.17 структурная схема относится к режиму измере­ния частоты. Работа схемы заключается в следующем.

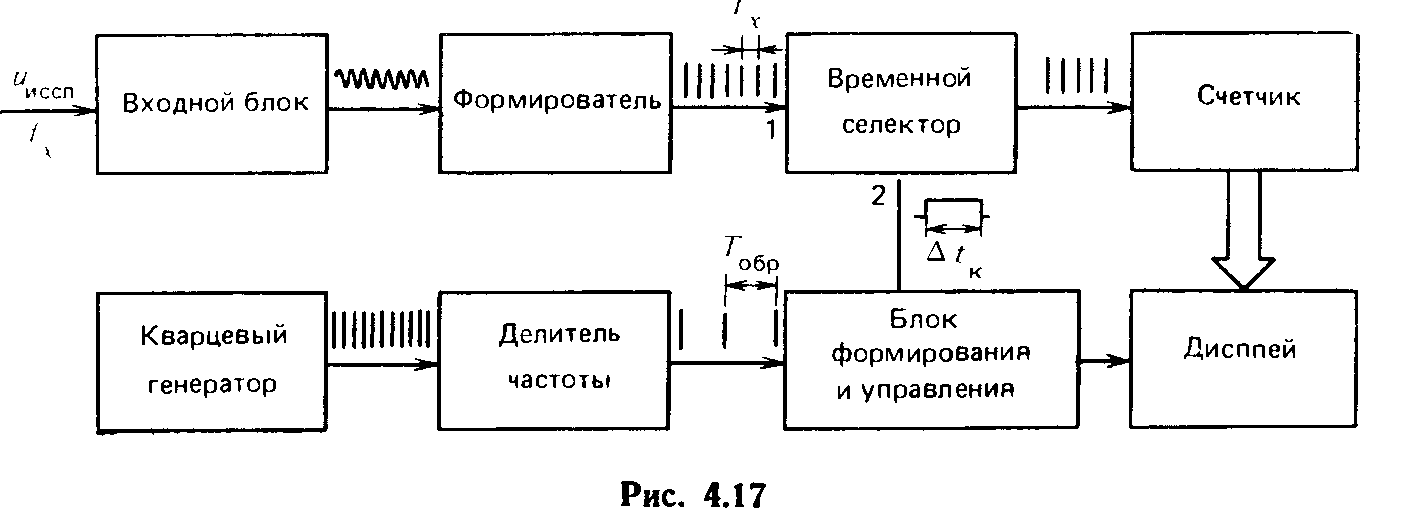
Периодический сигнал, частоту f_х которого необходимо изме­рить, поступает на вход прибора (обычно его обозначают бук­вой А). После усиления или ослабления во входном блоке сигнал подается на формирователь, где преобразуется в периодическую последовательность импульсов с частотой следования f_х. Эти им­пульсы подводятся к входу 1 временного селектора и проходят через него в счетчик, если на входе 2 селектора имеется стробирующий импульс (длительностью М_к). Последний формируется из напряжения высокочастотного кварцевого генератора. Так как период его выходного сигнала мал, то для получения требуемом длительности стробирующего импульса (например, 1 с) в схеме предусмотрен делитель частоты. Он представляет собой набор де­кад, каждая из которых уменьшает частоту следования импульсов в 10 раз. Коэффициент деления g зависит от числа включенных декад. Из периодической последовательности импульсов, образу­ющейся на выходе делителя частоты, блок формирования и уп­равления формирует стробирующий импульс (временные ворота) длительностью Δtк, подаваемый на вход 2 временного селектора и определяющий продолжительность счета. Блок формирования и управления, помимо формирователя временных ворот, содержит схему, задающую продолжительность индикации показания дис­плеем и сбрасывающую показания счетчика на нуль.

Погрешности измерения. При прямом измерении частоты пе­риодического сигнала наиболее весомы две составляющие погреш­ности: погрешность меры и погрешность сравнения.

Погрешность меры определяется нестабильностью частоты на­пряжения кварцевого генератора (а также погрешностью установ­ки частоты по образцовой мере при изготовлении прибора). Эта составляющая погрешности может быть ощутимой при измерении очень высоких частот. В современных цифровых частотомерах применяются кварцевые генераторы с малой нестабильностью частоты, например, ±1 • 10^-10 за 1 с и ±5 -10^-9 за сутки.

Погрешность сравнения определяется главным образом по­грешностью дискретности, обусловленной тем, что фронт и срез стробирующего импульса (временных ворот) не синхронизирова­ны с моментами появления заполняющих ворота импульсов пе­риодической последовательности, которая сформирована из иссле­дуемого сигнала. Максимальное значение абсолютной погрешно­сти дискретности составляет плюс-минус единицу дискретизации и не зависит от измеряемого значения частоты. Так как при изме­рении частоты за единицу дискретизации принято значение Fобр, то максимальная абсолютная погрешность дискретности при из­мерении частоты

(4-14)

Этому соответствует ±1 младшего разряда счета, причем зна­чение Δf выражено в герцах, если интервал Δtк выражен в се­кундах.

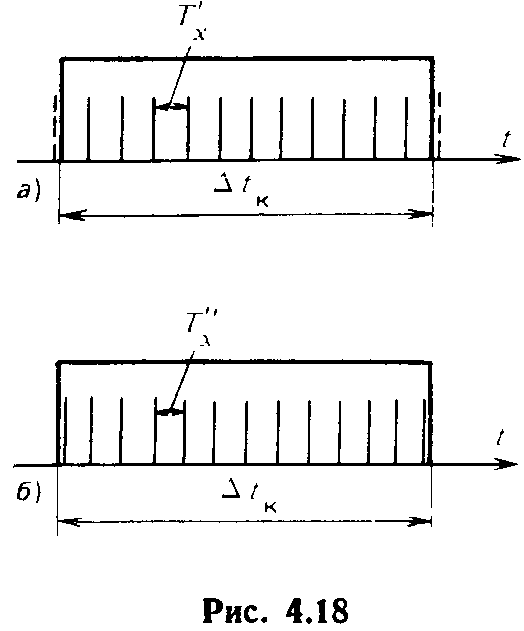
Чтобы убедиться в сказанном, вос­пользуемся рис. 4.18, где изображены две экстремальные ситуации. Если вы­полняется точно равенство (4.13) или соответственно соотношение Δt_к/Т_х = п, то это означает, что в интервале Δt_к укладывается точно n периодов Т_х ис­следуемого сигнала. В рассматривае­мом примере п= 12.

Теперь предположим, что измеряе­мая частота f'_х = f_х, но f_х чуть ниже Соотношение между Т'_х=1/f'_х и Δt_к такое, как показано на рис. 4.18,а. При этом значение f'_х измеряемой частоты определится из соотношения f'_х = п'/Δt_к и показание прибора будет A'_п=(n—1)/Δt_к. Приняв f_х = п/Δt_к за действительное значение измеряемой частоты f'_х, най­дем, что абсолютная погрешность дискретности

Аналогично рассуждая для ситуации, иллюстрируемой рис. 4.18,6, когда f"_Х=f_Х, но f"_х чуть выше f_х, приходим к заключению, что хотя в интервале Δt_к фактически укладывается n= 12 перио­дов Т"_х, счетчик зафиксирует число n"=n+1=13. Значение f"_х измеряемой частоты находится из формулы f"_х=п"/Δt и показа­ние прибора Из оказанного следует, что для рассматриваемой ситуации абсолютная погрешность дискретно­сти

Таким образом, максимальное значение абсолютной погреш­ности дискретности при измерении частоты

Максимальное значение относительной погрешности дискрет­ности измерения частоты согласно (4.13) и (4.14)

(4.15)

Максимальная абсолютная прогрешность дискретности Δ_д=Δt_К определяет разрешающую способность цифрового час­тотомера. Поэтому весь набор клавиш, с помощью которых уста­навливается длительность Δt временных ворот, отмечен общей надписью РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ а у конкретных клавиш написаны значения 1/Δt_к = F_обр, выраженные в единицах частоты — герцах или килогерцах (замечание о нестрогости подоб­ного определения значения разрешающей способности см. сноску иа стр. 115).

Предел основной допускаемой абсолютной погрешности циф­рового частотомера характеризуется выражением

где бкв — общая погрешность меры (кварцевого генератора).

Предел основной допускаемой относительной погрешности, выраженной в процентах от измеряемого значения c учетом (4.13) определится формулой

Уменьшение погрешности дискретности. При измерении низких частот погрешность дискретности является определяющей состав­ляющей погрешности измерения. Например, если измеряется час­тота f_x = 5 Гц при Δt_к=1 с, то максимальное значение абсолют­ной погрешности дискретности +1 Гц, а максимальное значение относительной погрешности составит 20%, что недопустимо велико.

Таким образом, из-за больших погрешностей дискретности низкие частоты непосредственно измеряются цифровым частото­мером с невысокой точностью. Поэтому решение задачи уменьше­ния влияния погрешности дискретности на результате измерения всегда представляло одно из важных направлений разработки цифровой частото-измерительной техники. Прежде, чем рассмат­ривать цифровые частотомеры с микропроцессорами, радикально решающие указанную задачу, остановимся на четырех способах уменьшения погрешности дискретности при измерении частоты.

Первый способ очевиден: он сводится к увеличению длитель­ности временных ворот, т. е. продолжительности измерения. Но возможности такого способа ограничены, так, нередко для полу­чения высокой точности требуется очень большая продолжитель­ность измерения. В обычных цифровых частотомерах (не содер­жащих микропроцессоры) максимально возможная длительность временных ворот Δtк=10 с.

Второй способ сводится к увеличению числа импульсов, запол­няющих временные ворота, достигаемому умножением частоты исследуемого сигнала. При этом максимальная абсолютная по­грешность меняется (если неизменна длительность ворот), но уменьшается относительная погрешность. Осуществление данного способа сопряжено с применением дополнительного блока — ум­ножителя частоты, что усложняет и удорожает аппаратуру.

Третий способ, учитывающий случайную природу погрешности дискретности, предполагает проведение многократных наблюдений (единичных измерений) и усрденение их результатов. Это эффек­тивный путь уменьшения влияния случайной погрешности на ре­зультат измерения.

Четвертый способ заключается в непосредственном измерении периода исследуемого сигнала с последующим вычислением чис­лового значения, обратного результату измерения периода. Этот путь позволяет резко уменьшить погрешность дискретности при измерении низких частот.

Воспользуемся приведенным ранее примером, чтобы ощутить достигаемый эффект. Измеряемое значение частоты 5 Гц. При не­посредственном измерении относительная погрешность дискрет­ности составляла 20%, если Δt_к⁼1 с. Увеличение длительности ворот до 10 с приведет к тому, что указанная погрешность умень­шится до 2%, но это во многих случаях неприемлемо.

Перейдем к измерению периода. Частоте f_х = 5 Гц соответству­ет период T_x = 0,2 с. Заполним его счетными импульсами, частота следования которых 10 МГц (что обычно имеет место в цифро­вых частотомерах). Так как T_СЧ=10^-7 с, то относительная по­грешность дискретности измерения периода составит

Принимая во внимание, что при малых погрешностях измере­ния периода относительная погрешность измерения частоты рав­на относительной погрешности измерения периода, т. е.

, (4.16)

несложно заключить, что косвенное измерение частоты в данном случае позволило резко повысить точность по сравнению с пря­мым измерением частоты: относительная погрешность дискрет­ности уменьшилась в 400 000 раз.

Не следует забывать, что при пользовании обычными цифро­выми частотомерами для нахождения искомого значения частоты по результату измерения периода требуются вычисления, прово­димые вручную (с помощью микрокалькулятора).

В дальнейшем нам понадобится соотношение между абсолют­ными погрешностями дискретности Δf / Δ_T. Поскольку б=Δf / f_х и бт= Δ_T/T_x, то из равенства бf=бт следует, что

(4.17)