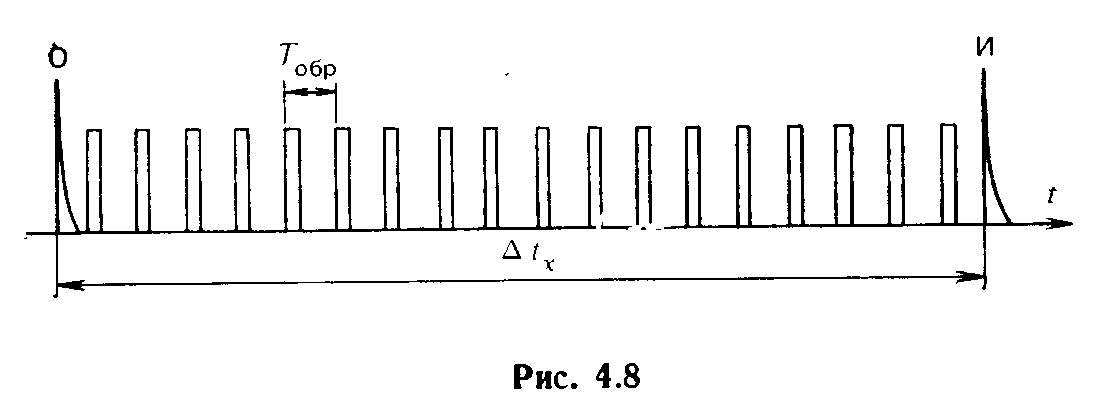
2. Измерение интервалов времени методом дискретного счета

Измерение, заключается в сравнении измеряемого интервала времени Δt_х с дискретным интервалом, воспроизводящим единицу времени. Для этого измеряемый интервал Δt_х заполняется импульсами с известным образцовым периодом следования (рис. 4.8), т. е. интервал преобразуется в отрезок периодической последовательности импульсов, число т которых, пропорциональ­ное М_х, подсчитывается. Импульсы, заполняющие интервал А/*, принято называть счетными и обозначать период их следования Т_сч. Таким образом,

Структурная схема измерителя. Для аппаратурного осуществ­ления описанного метода необходимы генератор счетных импуль­сов и счетчик, между которыми должна быть включена схема, от­крывающая счетчик на время Δt_х. Эту функцию, как видно из рис. 4.9, выполняет временной селектор, представляющий собой логический элемент И. Счетные импульсы, непрерывно поступа­ющие на вход 1 временного селектора, могут проходить в счетчик.

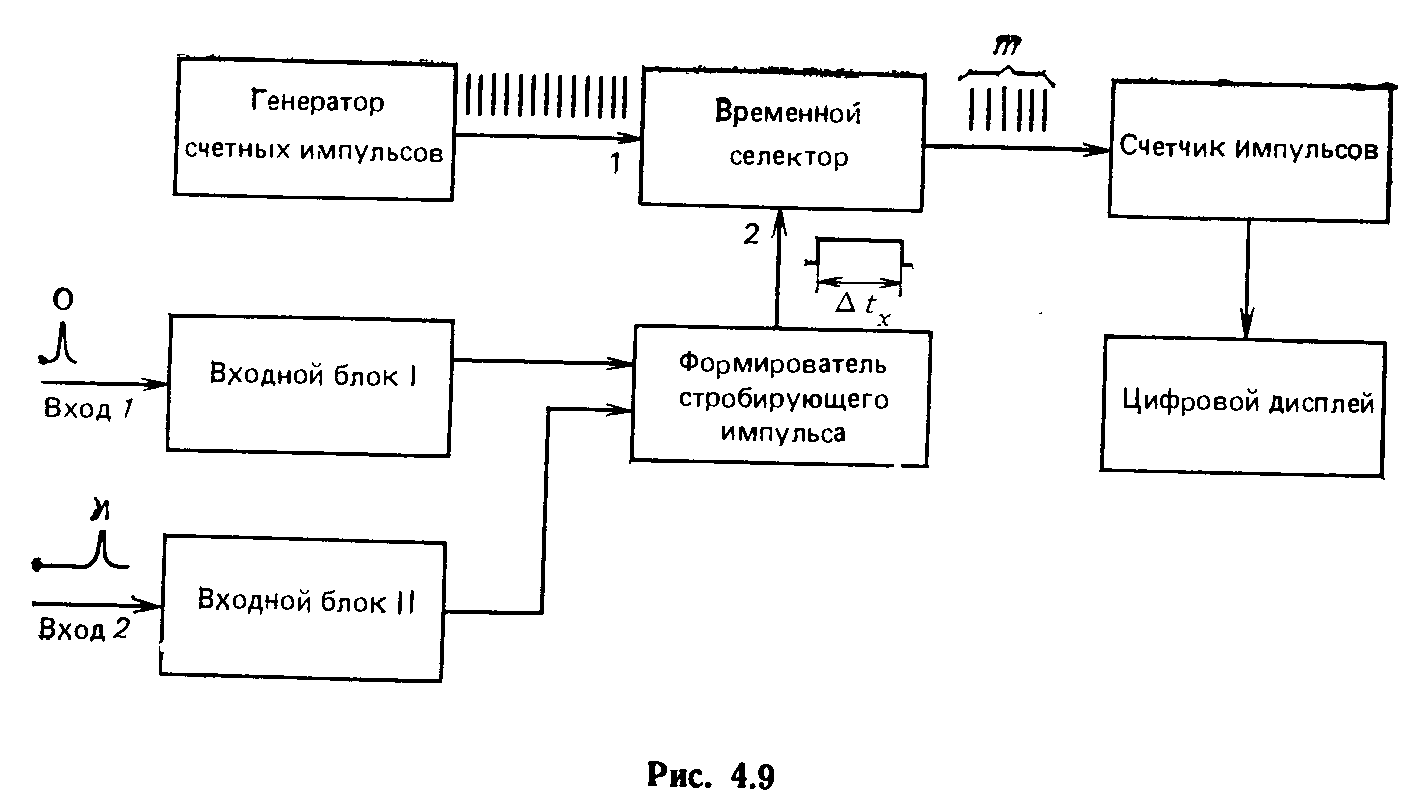
только тогда, когда на входе 2 селектора действует стробирующий импульс. Он формируется из исследуемого сигнала устройством, содержащимся в блоке формирования и управления. За время действия стробирующего импульса, длительность которого равна измеряемому интервалу ∆t_x (рис. 4.8), счетчик считает импуль­сы генератора. Число импульсов, зафиксированное счетчиком и наблюдаемое с помощью цифрового отображающего устройства — дисплея, однозначно соответствует измеряемому интервалу ∆t_х.

В измерительной технике импульс, вырезающий участок им­пульсной последовательности или задающий продолжительность счета, принято называть временными воротами.

Если период следования счетных импульсов генератора Т_сч (частота следования F_сч ), то за интервал ∆t_х, через временные во­рота пройдет

импульсов и, следовательно, измеряемый интервал

(4.2)

Измерения оказываются косвенными. Для получения прямого показания в приборах, построенных по схеме с жесткой логикой (без микропроцессора), частота следования импульсов выбрана равной Тогда

Таким же способом можно измерить и длительность прямо­угольного импульса τ_и. В этом случае исследуемый импульс по­дается непосредственно на вход 2 селектора. Временные ворота получаются равными длительности τ_и.

Интервал времени можно преобразовать в пропорциональное число импульсов и с помощью генератора ударного возбуждения. Для этого на вход последнего нужно подать стробирующий импульс, длительность которого равна измеряемому интервалу вре­мени, т. е За время действия стробирующего импульса генератор вырабатывает пакет импульсов, число р которых — однозначная функция частоты генерируемого сигнала и длитель­ности стробирующего импульса: Следовательно,

Погрешности измерения. Проанализируем погрешности, клас­сифицируя их по слагаемым измерения.

В схеме на рис. 4.9 мерой служит генератор счетных импуль­сов. Следовательно, погрешность меры в данном случае — это не­стабильность частоты следования импульсов. Для ее уменьше­ния генератор выполняют по схеме с кварцевой стабилизацией. Применяя генератор ударного возбуждения, следует иметь в ви­ду, что стабильность частоты варабатываемого им напряжения от­носительно невысока, и погрешность меры может оказаться зна­чительной.

Погрешность преобразования обусловлена главным образом шумовой помехой, проявляющейся при формировании стробирую­щего импульса (временных ворот) из опорного и интервального импульсов. Формирование производится с помощью триггерных схем. Так как крутизна фронта импульсов конечна, то в резуль­тате суммирования напряжения помехи с напряжениями опорно­го и интервального импульсов смещаются моменты перебросов триггера относительно моментов достижения этими импульсами уровня запуска в отсутствие помехи. Следовательно, длительность сформированных триггером временных ворот отличается от измеряемого интервала — появляется погрешность, которую называют погрешностью запуска триггера: Так как эта погрешность случайная, то ее характеризуют среднеквад­ратическим значением. При расчетах пользуются среднеквадра­тическим значением относительной погрешности, обозначаемым бзап- Погрешность измерения, обусловленная шумовой помехой, уменьшается с увеличением отношения крутизны фронта импуль­са к среднеквадратическому значению напряжения помехи, а так­же при усреднении результата q измерений интервала

Погрешность сравнения (измеряемого интервала с перио­дом следования Т_сч счетных импульсов) определяется тем, что из­меряемое значение интервала времени заменяется целым числом периодов следования счетных импульсов (с математической точ­ки зрения такая процедура подобна округлению чисел. Это — ме­тодическая погрешность, обусловленная дискретизацией непре­рывной величины — измеряемого интервала времени. Такую сос­тавляющую погрешности измерений называют погрешностью ди­скретности. Она возникает вследствие того, что стробирующий им­пульс длительностью и периодическая последовательность счет­ных импульсов в общем случае не синхронные сигналы.

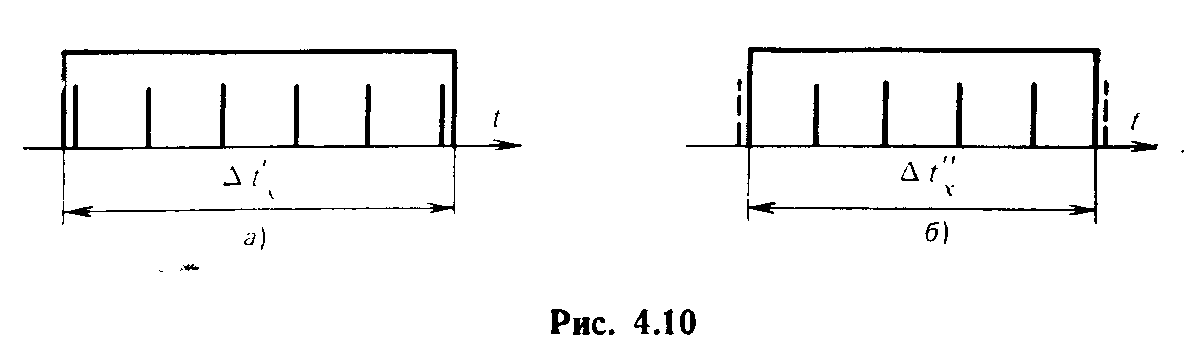
В реальной схеме измерения непосредственно фиксируется чи­сло попавших во временные ворота счетных импульсов, а не чи­сло периодов их следования и поэтому, вообще говоря, округ­ление может производиться в сторону как большего, так и меньшего значения ¹. Максимальное значение абсолютной погрешности дискретности (при правильно выбранной схеме стробирования) составляет плюс-минус один период следования счетных импуль­сов Т_сч. Это иллюстрирует рис. 4.10, на котором отражены две экстремальные ситуации.

Если равенство (4.1) выполняется точно, то это означает, что измеряемый интервал ∆t_х точно «вырезает» m периодов следова­ния счетных импульсов (для данного примера m=5). В случае, показанном на рис. 4.10,а, чуть больше

т. е. интервал практически равен m периодам Т_сч, счет­чик сосчитает т'=т+1=6 импульсов. При этом значение измеряемого интервала времени определится из соотношения и показание прибора будет . Если принять за действительное значение, то абсолютная по­грешность дискретности составит

Аналогично рассуждая для ситуации, показанной на рис. 4.6,6, когда чуть меньше , констатируем, что хо­тя интервал практически равен тТ_сч, счетчик сосчитает m"=m-1=4 импульса. Тогда интервал , показание при­бора будет , и абсолютная погрешность дискретно­сти составит

Таким образом, максимальное значение абсолютной погреш­ности дискретности при измерении интервалов времени

Абсолютная погрешность дискретности не зависит от значе­ния измеряемого интервала времени: она определяется единицей дискретизации, т. е. T_сч. Наибольшая относительная погрешность дискретности составляет

(4.4)

и, конечно, зависит от значения Δt_х.

Максимальная абсолютная погрешность дискретности определяет разрешающую способность цифрового измерителя ин­тервалов времени. Поэтому весь набор клавиш, с помощью кото­рых устанавливаются значения периода следования счетных им­пульсов, снабжен общей надписью РАЗРЕШАЮЩАЯ СПОСОБ­НОСТЬ, а конкретные клавиши отмечены значениями Т_сч, выра­женными в миллисекундах, микросекундах или десятичных до­лях их¹.

Погрешность дискретности по всей природе случайна и поэто­му о ее максимальном значении, разумеется, можно говорить толь­ко в вероятностном смысле. Погрешность дискретности складыва­ется из двух составляющих. Поскольку появление счетного им­пульса до фронта стробирующего импульса (временных ворот) равновероятно, как и равновероятно появление счетного импуль­са перед срезом временных ворот или после него, и эти две сос­тавляющие случайной погрешности независимы, то суммарная аб­солютная погрешность дискретности распределена в пределах по закону Симпсона (треугольному закону). При этом математическое ожидание погрешности равно нулю, а сред­неквадратическое значение Учитывая финитный характер распределения Симпсона, несложно заключить, что максималь­ная абсолютная случайная погрешность принимает значения ±T_СЧ с вероятностью 1.

Когда применяется измеритель интервалов времени, собранный по схеме LС-генератора ударного возбуждения, то счетные импульсы оказываются син­хронизированными с фронтом стробирующего импульса. Погрешность дискрет­ности распределена по равномерному закону. Ее максимальное значение мож­но уменьшить вдвое по сравнению е погрешностью предыдущего измерителя, если сдвинуть момент появления первого импульса генератора на половину пе­риода относительно фронта стробирующего импульса.

Погрешность фиксации результата сравнения не имеет места, если счетчик импульсов обладает достаточно большой емкостью (может зафиксировать все импульсы, заполняющие интервал вре­мени) и высоким быстродействием.

Предел абсолютной допускаемой основной погрешности циф­рового измерителя интервалов времени

где -относительная нестабильность частоты напряжения кварцевого генератора; — измеряемый интервал; Т_сч — пери­од следования счетных импульсов; -среднеквадратическая относительная погрешность запуска.

Соответственно предел допускаемой основной относительной погрешности, выраженной в процентах от измеряемого значе­ния :

(4-6)

где т — число счетных импульсов, заполняющих интервал време­ни Δtx•

В (4.5) и (4.6) первые слагаемые — погрешности меры, тре­тьи— погрешности дискретности. Влияние первой составляющей сказывается сильнее при измерении интервалов большой длитель­ности, третьей составляющей — при измерении интервалов малой длительности.

Получим формулу для определения минимального интервала времени при заданной относительной погрешности дискретности и данной частоте следова­ния счетных импульсов (или быстродействии счетчика). Если измеряемый ин­тервал заполняют т. импульсов, то при абсолютной погрешности дискрет­ности относительная погрешность

(4.7)

Принимая во внимание соотношение (4.2), получаем

. (4.8)

Например, если то равна 0,2, или 20%.

Минимальный интервал времени, который можно измерить с погрешностью, меньшей или равной при частоте следования Fсч счетных импульсов,

(4-9)

где — в секундах; F— в герцах, а — в относительных единицах. На­пример, при минимальный интервал времени, измеряемый о максимальной погрешностью дискретности, не превосходящей 0.01

Уменьшение погрешности дискретности. Из приведенных фор­мул и примеров следует, что измерения малых интервалов време­ни могут сопровождаться значительными погрешностями дискрет­ности. Ее можно уменьшить тремя способами.

Первый способ, представляющий прямое, очевидное решение задачи — увеличение частоты следования счетных импульсов. Это требует применения не только генератора сигналов более высокой частоты, но и счетчика со значительно большим быстродействием, т. е. серьезного усложнения аппаратуры. Следовательно, возмож­ности использования первого способа существенно ограничены.

Второй способ заключается в измерении большого числа ин­тервалов т. е. интервала времени, равного Эта возмож­ность предусматривается в современных цифровых измерителях. Исследуемый периодический сигнал, представляющий периодиче­скую последовательность импульсов, с периодом следования

поступает в делитель частоты с коэффициентом деления q. На вы­ходе делителя получается периодическая последовательность им­пульсов, следующих с периодом . Хотя при неизменной часто­те следования счетных импульсов максимальное значение абсолютной погрешности дискретности остается тем же, что и при измерении одного интервала максимальная относительная по­грешность дискретности в случае измерения интервала времени уменьшается в q раз. Напомним, что при увеличении интер­вала в соответствующее число раз уменьшается и относитель­ная погрешность запуска триггера.

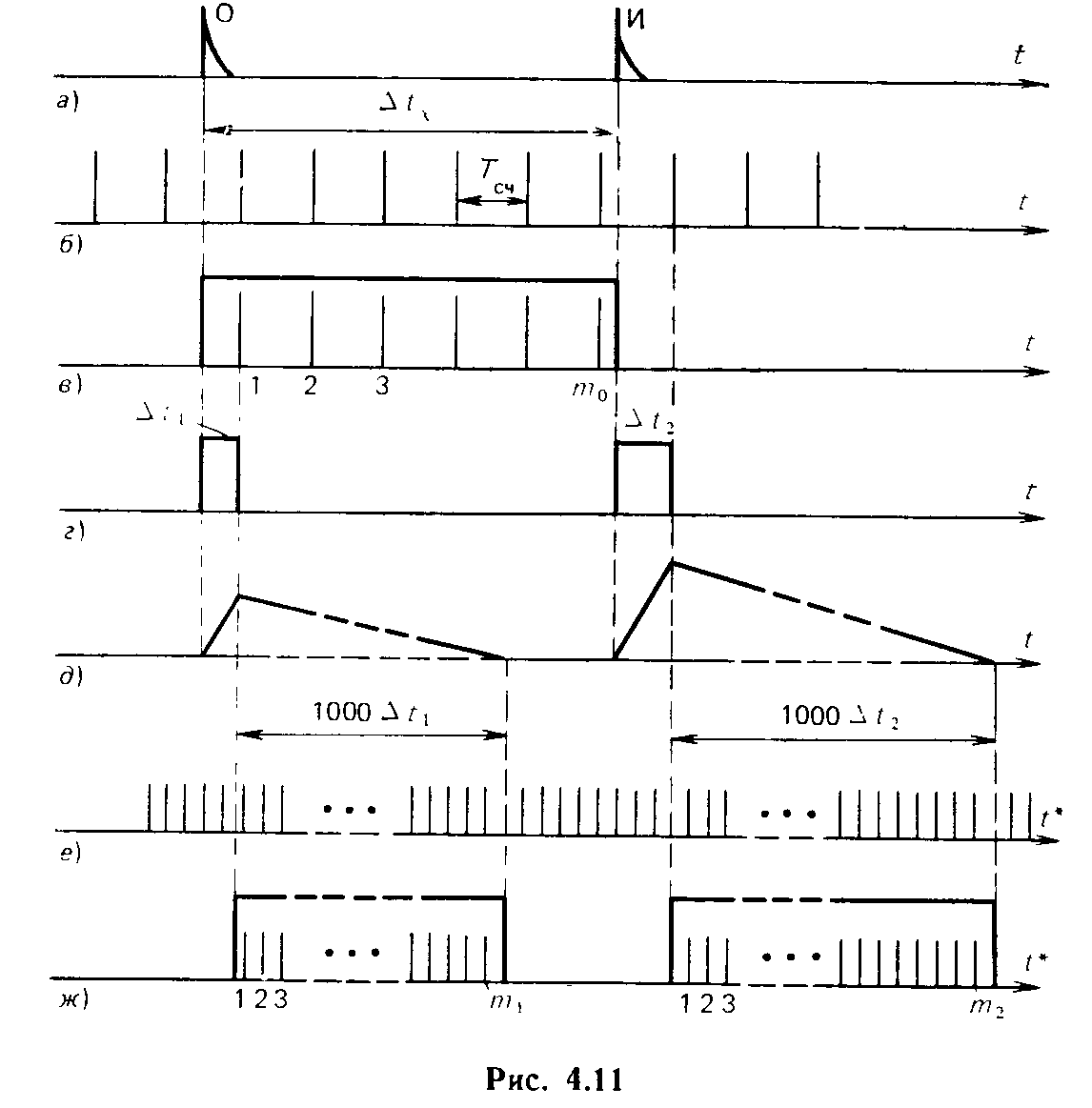
Третий способ, называемый интерполяцией, состоит в том, что помимо целого числа периодов счетных импульсов, заполняющих измеряемый интервал времени, учитываются и дробные части пе­риода, заключенные между опорным импульсом и первым счет­ным импульсом, а также между последним счетным импульсом и интервальным. Принцип осуществления этого способа иллюстри­рует рис. 4.11.

На рис. 4.11, а показаны опорный и интервальный импульсы, задающие измеряемый интервал на рис. 4.11,6 — счетные им­пульсы, следующие С периодом Tсч (частотой Fсч). Эти импульсы заполняют временные ворота (рис. 4.11,в). Число импульсов m₀. Первый счетный импульс, попавший в ворота, запаздывает относительно их фронта на время а срез ворот и очередной счетный импульс, появляющийся после среза, разделяет интервал (рис. 4.11,6—г). Следовательно, измеряемый интервал време­ни определяется соотношением

Поэтому если бы удалось точно учесть отрезки и то погрешность дискретности была бы исключена. Задача измерения интервалов и решается следующим образом.

За время линейно заряжается конденсатор, который затем разряжается в 1000 раз медленнее, т. е. время разряда составля­ет 1000 (рис. 4.11,д). Этот интервал заполняется теми же счет­ными импульсами (период следования Т_сч), и подсчитывается их число т₁ (рис. 4.11,е и ж)¹. Аналогичным образом «растягивается» отрезок . Полученный интервал 1000 также заполняется счетными импульсами, число которых составляет т₂. Так как то подстановка значений дает

Обозначим Тогда

Из полученного выражения видно, что интервал времени измеряется с абсолютной погрешностью дискретности что равносильно заполнению его счетными импульсами с частотой, в 10³ раз больше . Теперь уже интервал времени мкс при будет измеряться с относительной погрешностью дискретности δ= 0,0002, т. е. 0,02%, а не 20%. Для получения та­кой точности при прямом способе измерения понадобились бы счетные импульсы с частотой следования 10 ГГц и счетчик с еще более высоким быстродействием.

Измерение периода периодического сигнала. Это частный слу­чай общей задачи измерения интервалов времени. По отношению к периоду периодического сигнала моменты положений опорного и интервального импульсов на оси времени — это моменты двух соседних переходов исследуемого сигнала через нулевой уровень с производной одинакового знака, например положительного (пе­ресечения оси времени снизу вверх, рис. 4.12). Из сказанного не следует делать заключения, что для измерения периода синусои­дального сигнала или длительности прямоугольного импульса обя­зательно требуется преобразование этих сигналов в два коротких импульса.

Принцип измерения периода синусоидального сигнала мето­дом дискретного счета иллюстрирует рис. 4.13. Исследуемый сигнал

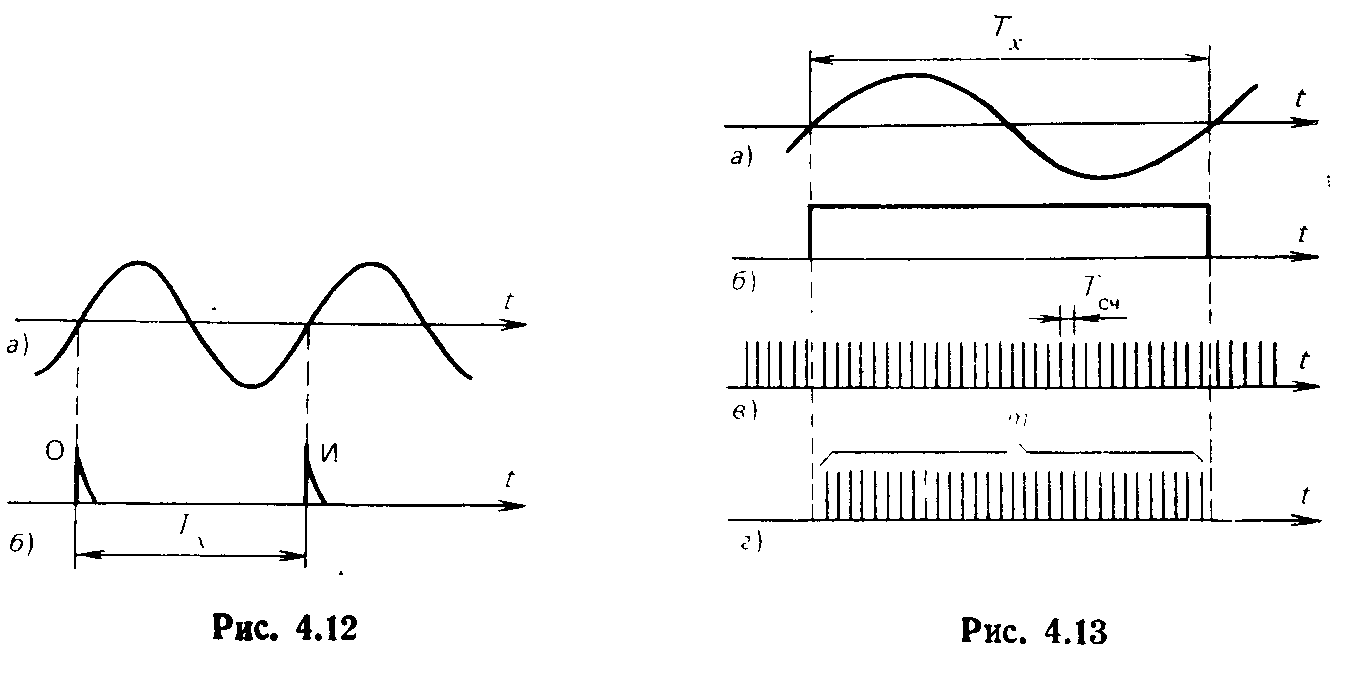
(рис. 4.13,а) преобразуется в прямоугольный импульс (рис.4.13 б) , который «вырезает» из периодической последовательности счетных импульсов (рис. 4.13,в) участок, содержащий т импуль­сов (рис. 4.13,г). Так как период их следования Т_сч, то значение измеряемого периода Т_х = тТ_сч.

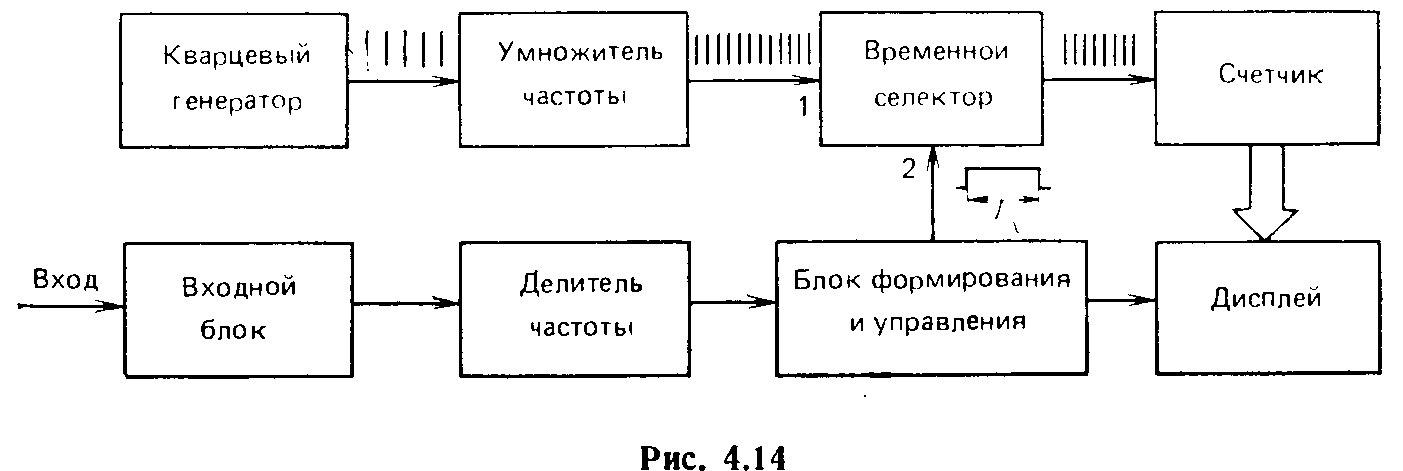
Структурная схема устройства для измерения периода пред­ставлена на рис. 4.14. Это — схема цифрового частотомера в ре­жиме измерения периода. Из исследуемого сигнала, период Т_х которого необходимо измерить, во входном блоке формируется периодическая последовательность коротких импульсов с перио­дом следования Т_х. В блоке формирования и управления из них формируется прямоугольный стробирующий импульс длительно­стью Т_х (рис. 4.13). Если включен делитель частоты с коэффици­ентом деления q, то время следования импульсов на его выходе получается равным qТ_х и такую же длительность, разумеется, имеет стробирующий импульс. Он подводится к входу 2 времен­ного селектора, на вход 1 которого подаются импульсы кварцево­го генератора, являющиеся счетными импульсами. Частота их следования Таким образом, Измеряемый период связан с показанием счетчика m и частотой кварцевого генератора соотношением

Составляющие погрешности измерения периода периодическо­го сигнала принципиально те же, что были рассмотрены при ана­лизе измерения интервалов времени, заданного опорным и интер­вальным импульсами.

Максимальная абсолютная погрешность дискретности Δт = ±Tсч, а соответствующая относительная погрешность δт= ΔT/Т_х=±1/m. Когда измеряется q периодов, то относительная погрешность дискретности уменьшается в q раз.

При измерении периода значительный вклад в общую погреш­ность может внести составляющая, обусловленная действием шу­мовой помехи при формировании стробирующего импульса — по­грешность запуска триггера. При расчетах пользуются среднеква­дратическим значением относительной погрешности δзап. Можно показать [46], что при измерении периода

где q — число одновременно измеряемых периодов сигнала; U_пом — среднеквадратическое значение напряжения помехи, U_т — ампли­туда напряжения сигнала, h = U_т/ U_пом — отношение сигнал-по­меха.

Например, при отношении сигнал-помеха 40 дБ (h=100) и q = 1 относительная среднеквадратическая погрешность δ_зап~0,3%. Если при том же отношении измерять интервал времени, равный 100 периодов сигнала, то δ_зап~0,003%.

Предел относительной допускаемой погрешности цифрового измерителя периода, выраженной в процентах по отношению к Т_х, определяется формулой

где δкв — общая погрешность меры (кварцевого генератора).