§2.4. Дисперсія світла

Дисперсією світла називається залежність показника заломлення n середовища від частоти (довжини хвилі ) світла або залежність фазової швидкості світла в середовищі від його частоти .

Дисперсію світла представляють у вигляді залежності . Наслідком дисперсії є розклад у спектр пучка білого світла.

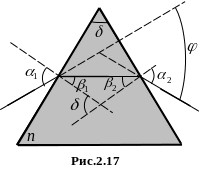
Розглянемо дисперсію світла у призмі. Нехай монохроматичний пучок світла падає на призму з показником заломлення n під кутом (рис. 2.17). Кут – заломлюючий кут призми. Із рис. 2.17 видно, що кут відхилення дорівнює:

.

Нехай кути і малі, тоді кути , і також будуть малі і синуси цих кутів дорівнюватимуть кутам. Тому

, .

Оскільки , то

,

і .

В результаті

, (2.48)

тобто кут відхилення променів призмою тим більший, чим більший заломлюючий кут призми. Оскільки кут відхилення залежить від величини , а n є функцією довжини хвилі, то промені різних довжин хвиль після проходження призми виявляються відхиленими на різні кути.

Кутовою дисперсією призми, що відповідає сталому значенню кута падіння , називається величина

. (2.49)

Кут відхилення буде мінімальним, коли промінь проходить через призму паралельно до її основи. За такої умови і , тоді

, а .

Згідно із законом заломлення

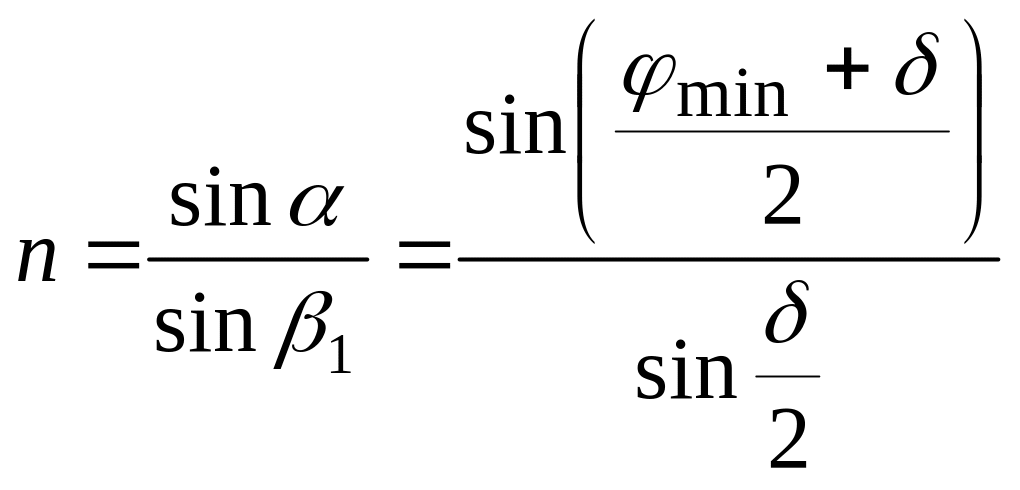. (2.50)

Звідси

.

Тоді

. (2.51)

Для спектральних приладів призми виготовляють здебільшого із заломлюючими кутами . Тоді

, де . (2.52)

За допомогою призми, як і за допомогою дифракційної гратки можна визначити спектральний склад світла.

Величина, яка показує, як швидко змінюється показник заломлення п речовини з довжиною хвилі називається дисперсією речовини D:

. (2.53)

Дисперсію світла в середовищі називають нормальною, якщо із зростанням частоти світла абсолютний показник заломлення n середовища також зростає:

, .

Така залежність показника заломлення n від буде в тих областях частот, для яких середовище прозоре. Наприклад, звичайне скло прозоре для видимого світла і в цьому інтервалі частот має нормальну дисперсію.

Дисперсію світла в середовищі називають аномальною, якщо із зростанням частоти світла абсолютний показник заломлення середовища n зменшується:

, .

Аномальна дисперсія буде в області частот, які відповідають смугам інтенсивного поглинання світла речовиною

В різних ділянках спектра дисперсія характеризується тією зміною показника заломлення, яка припадає на одиничний інтервал довжин хвиль. Ця величина називається середньою дисперсією для ділянки спектра , .

У довідникових таблицях показники заломлення різних речовин даються для жовтої лінії натрію =0,5893мкм і позначаються . Середня дисперсія визначається за синьою =0,4861мкм і червоною =0,6563мкм лініях водню і позначається . Величина називається відносною дисперсією, обернена її величина – коефіцієнтом дисперсії.