Логический базис.
Логические функции могут быть реализованы простейшими логическими элементами. Совокупность логических элементов И, ИЛИ, НЕ, с помощью которых можно воспроизвести и реализовать любую ФАЛ, будем называть полным логическим базисом.
Базис И, ИЛИ, НЕ обладает избыточностью и не является минимальным. Из этой совокупности ЛЭ можно исключить логический элемент И (либо ЛЭ ИЛИ), тогда наборы И, НЕ и ИЛИ, НЕ также будут обладать свойством базиса.
При проектировании логических схем вычислительной техники самое широкое применение получили базис Шеффера И-НЕ и базис Пирса ИЛИ-НЕ, обладающие свойством логического базиса.
Следует отметить, что одну и ту же логическую функцию (операцию) можно реализовать в различных базисах. Покажем это на примерах простых логических операций дизъюнкции и конъюнкции:
;
.
(7)
Используя законы
инверсии
и
,
преобразуем логические выражения
:
;
.
(8)
Выражения (7) отражают принцип двойственности алгебры логики: если в логическом выражении операцию дизъюнкции заменить на операцию конъюнкции (либо наоборот) и проинвертировать все переменные, то результат окажется инверсным прежнему значению.
Используя принцип двойственности алгебры логики, реализуем логическое выражение (7) в различных базисах.
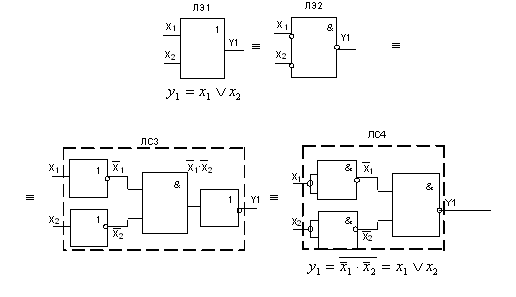
Рис. 2
Из рис.2 следует:
если переименовать все входы и выходы
логического элемента ЛЭ1 на инверсные
значения и заменить ЛЭ
дизъюнкции на ЛЭ2 конъюнкции, то функции
дизъюнкции можно выполнить с помощью
элементов НЕ, И (ЛС3) либо базиса Шеффера
И-НЕ (ЛС4).
Все логические схемы (рис. 2) выполняют логическую операцию (функцию) ИЛИ, которую можно реализовать на однотипных логических элементах И-НЕ, а при наличии инверсных сигналов в проектируемом устройстве – на одном ЛЭ И-НЕ.
На рис. 2 ЛС3 и ЛС4 – логические схемы, в состав которых входят несколько логических элементов ЛЭ.
Аналогично можно показать, что логическую операцию (функцию) И можно выполнить в базисах НЕ, ИЛИ либо в базисе Пирса ИЛИ-НЕ (рис. 3).
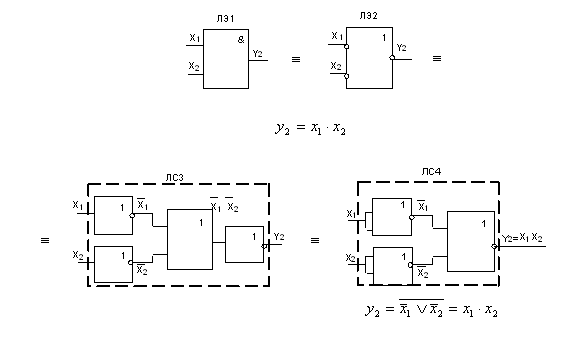
Рис. 3
Таким образом, логический базис, представляющий собой совокупность типов логических элементов, может быть выполнен на универсальных логических элементах И-НЕ и ИЛИ-НЕ, выпускаемых промышленностью в интегральном исполнении. Полный логический базис И, ИЛИ, НЕ обычно используется на начальной стадии проектирования функциональных узлов для составления функциональных схем.
Минимизация логических функций.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки. В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.