6.Алгоритми на графах.
Задача Прима-Краскала
Даний граф з n вершинами. Довжини ребер задані матрицею {cij}, де i, j = 1,…,n. Зайти остовне дерево мінімальної ваги.
Остовним деревом для графа називається неорієнтоване дерево, яке містить всі вершини графа. Вартість або вага остовного дерева визначається як сума вартостей його ребер.
Алгоритм Прима-Краскала
Спочатку покрасимо i-у вершину в відмінний від інших колір i, тобто всі вершини різнокольорові. Для побудови остовного дерева мінімальної ваги необхідно кожного разу обирати вершини різного кольору, відстань між якими найменша. При виборі такого чергового ребра найменшої довжини (i, j) вершина j та всі вершини її кольору (тобто раніше з нею з’єднані) перекрашуються в колір i. Таким чином вибір вершин різного кольору забезпечує відсутність циклу. Після вибору (n-1) ребер всі вершини отримують один колір.
Приклад. Знайти дерево мінімальної ваги для заданого графа:
20
1
2
23 1 4 15
36 9
6 7
3
25 16
28 3
5 4
17
1 7 – колір вершин 1, відстань 1;
3 4 – колір вершин 3, відстань 3;
7 2 – колір вершин 1, відстань 4;
7 3 – колір вершин 1, відстань 9;
4 5 – колір вершин 1, відстань 17;
1 6 – колір вершин 1, відстань 23.
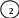
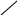
Вага остовного дерева: 1+3+4+9+17+23 = 57.
Варіанти індивідуальних завдань
Графи
1.Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 4,5 6,7 3,5 2,8 3,6
4,5 0 5,1 4,5 6,3 7,0
6,7 5,1 0 1,8 3,1 8,2
3,5 4,5 1,8 0 6,5 7,3
2,8 6,3 3,1 6,5 0 9,0
3,6 7,0 8,2 7,3 9,0 0
2.Знайдіть остове дерево мінімальної ваги для графа:
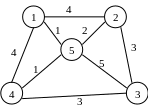
3.Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 3 9 5 8
3 0 7 6 4
7 0 1 2
5 6 1 0 4
8 4 2 4 0
4.Знайдіть остове дерево мінімальної ваги для графа:
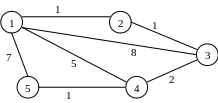
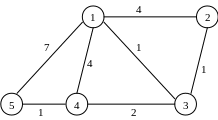
5.Знайдіть остове дерево мінімальної ваги для графа:
6. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 9,5 8,6 10,8 8,9 7,1 14
9,5 0 14,6 8,6 17 8,9 6,4
8,6 14,6 0 9,5 15 15,6 20,6
10,8 8,6 9,5 0 19,7 15 14,9
8,9 17 15 19,7 0 9,5 19,3
7,1 8,9 15,6 15 9,5 0 9,8
14 6,4 20,6 14,9 19,3 9,8 0
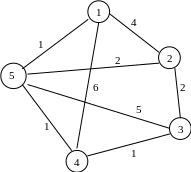
7.Знайдіть остове дерево мінімальної ваги для графа:
8. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 3,8 9,1 14 4,9
3,8 0 7,2 3,8 13
9,1 7,2 0 7,2 11
14 3,8 7,2 0 4,9
4,9 13 11 4,9 0
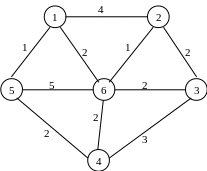
9. Знайдіть остове дерево мінімальної ваги для графа:
10. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 4,8 1,1 25 13,2
4,8 0 1,8 1,1 10
1,1 1,8 0 2,5 3,1
25 1,1 2,5 0 2,5
13,2 10 3,1 2,5 0
11. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 7,8 1,1 25 13,2
7,8 0 3,8 1,1 10
1,1 3,8 0 2,5 3,9
25 1,1 2,5 0 8,5
13,2 10 3,9 8,5 0
12.Знайдіть остове дерево мінімальної ваги для графа:
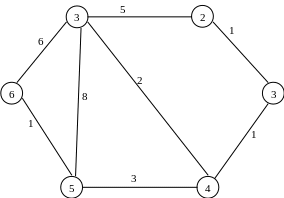
Знайдіть остове дерево мінімальної ваги для графа:
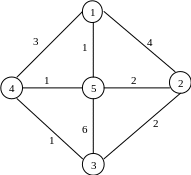
14. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
3,1 2,5 6,7 8,1
3,1 0 5,4 3,3 4,7
2,5 5,4 0 2,8 7,9
6,7 3,3 2,8 0 7,1
8,1 4,7 7,9 7,1 0
15. Знайдіть остове дерево мінімальної ваги для графа:
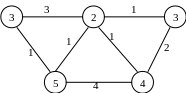
16. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 1,1 4,5 6,3 3,7
1,1 0 2,9 5,6 4,1
4,5 2,9 0 6,7 8,1
6,3 5,6 6,7 0 7,0
3,7 4,1 8,1 7,0 0
17. Знайдіть остове дерево мінімальної ваги для графа:
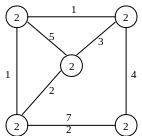
18. Знайдіть остове дерево мінімальної ваги для графа:
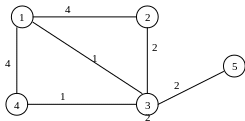
19.Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 3 8 4 6
3 0 2 1 5
8 2 0 7 9
4 1 7 0 6
6 5 9 6 0
20. Знайдіть остове дерево мінімальної ваги для графа, заданого матрицею:
0 5,5 6,6 7,7 8,8
5,5 0 4,4 2,2 3,3
6,6 4,4 0 1,1 9,9
7,7 2,2 1,1 0 1,5
8,8 3,3 9,9 1,5 0