3.4. Кинематический анализ сооружения

Как отмечалось выше сооружение или система могут быть геометрически неизменяемыми (напр. простая ферма из 3-х стержней) или изменяемыми (ферма, состоящая из 4-х стержней).

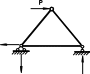
Геометрически неизменяемая Геометрически изменяемая

система (сооружение) система (механизм)

При расчете любого сооружения необходимо в первую очередь убедиться в его геометрической неизменяемости.

Изменяемость системы характеризуется ее степенью свободы.

Степенью свободы W, называется количество независимых параметров, которые в любой момент времени определяют положение системы на плоскости или в пространстве.

Рассмотрим степень свободы стержня. Его положение на плоскости определяется тремя независимыми параметрами X, Y и углом поворота .

Рассмотрим 2 стержня, соединенных между собой шарниром. Чтобы судить о положении стержней на плоскости, надо использовать 4 параметра, т.е. система имеет 4 степени свободы.

Если бы отсутствовал соединительный шарнир "В", то стержни имели бы 6 степеней свободы, каждый по 3. Таким образом, шарнир, соединяющий два стержня между собой, уменьшает степень свободы системы на 2 и называется простым шарниром.

Рассмотрим теперь 3 стержня, соединенных между собой шарниром "В". Без шарнира система имела бы 9 степеней свободы, а с шарниром - 5. Значит такой шарнир уменьшает степень свободы системы на 4 единицы, т.е. он эквивалентен двум простым шарнирам.

Шарниры, соединяющие 3 и более стержней называются сложными или кратными.

Как видно из этих примеров, шарнир, соединяющий n стержней, эквивалентен числу (n-1) простых шарниров.

Можно записать:

,

здесь: D – число дисков в рассматриваемой системе, Ш₀ – число простых шарниров.

Пример. Д=7; Ш₀=9;

Тогда W = 3*7 – 2*9 = 3

Поскольку все возводимые конструкции должны быть неподвижными, поэтому необходимо прикрепить к основанию или земле с помощью опорных связей (опорных стержней).

В первом случае диск имеет две степени свободы. При креплении диска двумя опорными связями, возможен только его поворот вокруг точки А. Таким образом, диск имеет одну степень свободы.

Наложим 3 связи - все возможные перемещения диска исключены.

Вывод: каждый опорный стержень уменьшает степень свободы диска или системы дисков на 1 единицу.

Окончательно:

W = 3D – 2Ш₀ – С_ОП ,

где: Д - число дисков (стержней) системы, Ш₀ – число простых шарниров,

С_ОП - количество опорных стержней.

Следует помнить:

1. W>0 - система подвижная, т.е. геометрически изменяемая;

2. W=0 - система геометрически неизменяема и статически определима.

3. W<0 - система геометрически неизменяема и статически неопределима.

Примеры.

1)Д=7; Ш₀=9; С_ОП=3; W=0, т.е. ферма, прикрепленная к земле, геометрически неизменяема.

2)Д=2; Ш₀=1; С_ОП=9; W=5, т.е. рассматриваемая система имеется 5 "лишних" связей.

Следует помнить:

1. W>0 - система подвижная, т.е. геометрически изменяемая;

2. W=0 - система геометрически неизменяема и статически определима.

3. W<0 - система геометрически неизменяема и статически неопределима.