2.2 Определение критической силы. Формула эйлера

Впервые проблема устойчивости сжатых стержней была поставлена Леонардом Эйлером. Эйлер вывел расчетную формулу для критической силы и показал, что ее величина существенно зависит от способа закрепления стержня. Идея метода Эйлера заключается в установлении условий, при которых кроме прямолинейной возможна и смежная (т.е. сколь угодно близкая к исходной) криволинейная форма равновесия стержня при постоянной нагрузке.

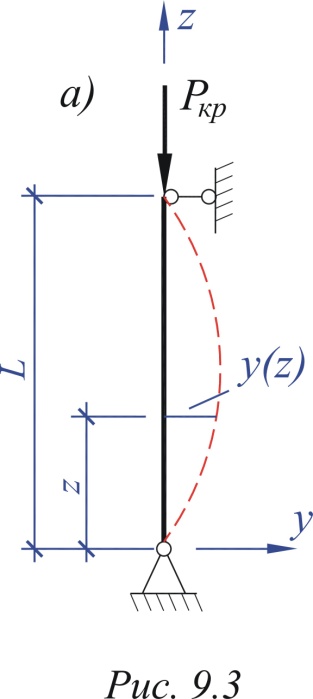
Рис.2.3.

Предположим, что шарнирно закрепленный по концам прямой стержень, сжатый силой P=Pкр, был выведен некоторой горизонтальной силой из состояния прямолинейного равновесия и остался изогнутым после устранения горизонтальной силы (рис. 2.3). Если прогибы стержня малы, то приближенное дифференциальное уравнение его оси будет иметь такой же вид, как и при поперечном изгибе бруса: , Mx­­=-Pкрy, откуда . Обозначим , тогда получим . Решение данного дифференциального уравнения имеет вид:

Из условий внешнего закрепления стержня на опорах имеем:

у(0)=0, откуда получим B=0;

у(L)=0, откуда получим А sinkL=0.

Очевидно, что А не может быть равным нулю, поскольку в этом случае прогибы во всех точках будут равны нулю. Получим

sinkL=0, откуда

kL=n, где nZ.

, где nZ.

Делая обратную замену, получим

, откуда получим выражение для критической силы

.

Величина nZ является порядковым номером формы потери устойчивости. На практике, как правило, используется самая первая форма потери устойчивости, поскольку она указывает на сам факт перехода коснтрукции в иное, возможно непредстказуемое состояние.

Выпучивание стержня происходит в сторону наименьшей жесткости, если нет специальных устройств, препятствующих изгибу стержня в этом направлении. Поэтому в полученную формулу надо подставлять I_min - меньшей из главных центральных осевых моментов инерции поперечного сечения стержня.

Принимая n=1, получим

.

(2.1)

Полученная формула, позволяет определить величину критической силы шарнирно закрепленного стержня, и носит название формулы Эйлера.

Формула (2.1), как следует из ее вывода, справедлива не только для стержня с шарнирно закрепленными концами, но и для любого стержня, который изогнется при выпучивании по целому числу полуволн. Применим эту формулу, например, при определении критической силы для стержней, показанных на рис. 2.4. Очевидно, что число полуволн изогнутой оси, поместившихся на длине L, для схемы показанной на рис. 2.4,а равно двум. Длина полуволны, которую будем называть расчетной длиной L_p, будет равна , т.е. . Для схемы на рис. рис. 2.4,б на длине L уместилась всего лишь половинка полуволны синусоиды. Тогда расчетная длина в этом случае будет равна . Обобщая на все возможные закрепления стержня, введем понятие коэффициента приведения длины - , который будет равен .

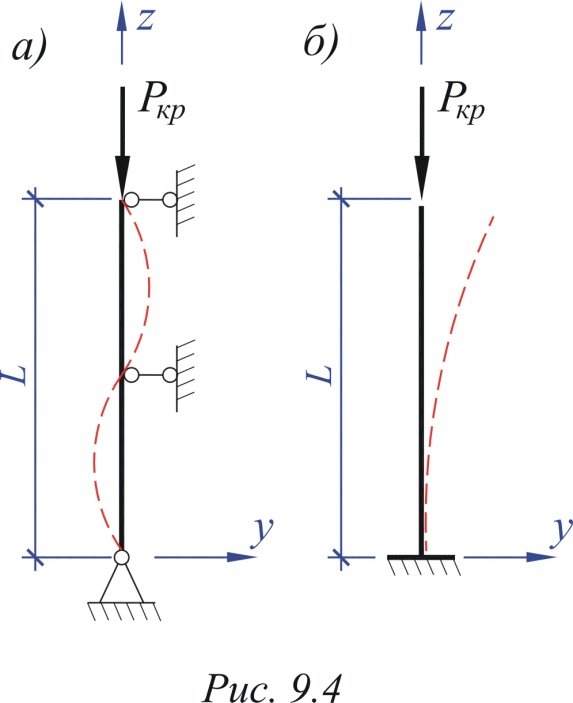
Рис.2.4.

Для большинства случаев внешних опор стержня коэффициенты приведения длины посчитаны и приведены в справочных пособиях. Некоторые из них приведены на рис. 2.5.

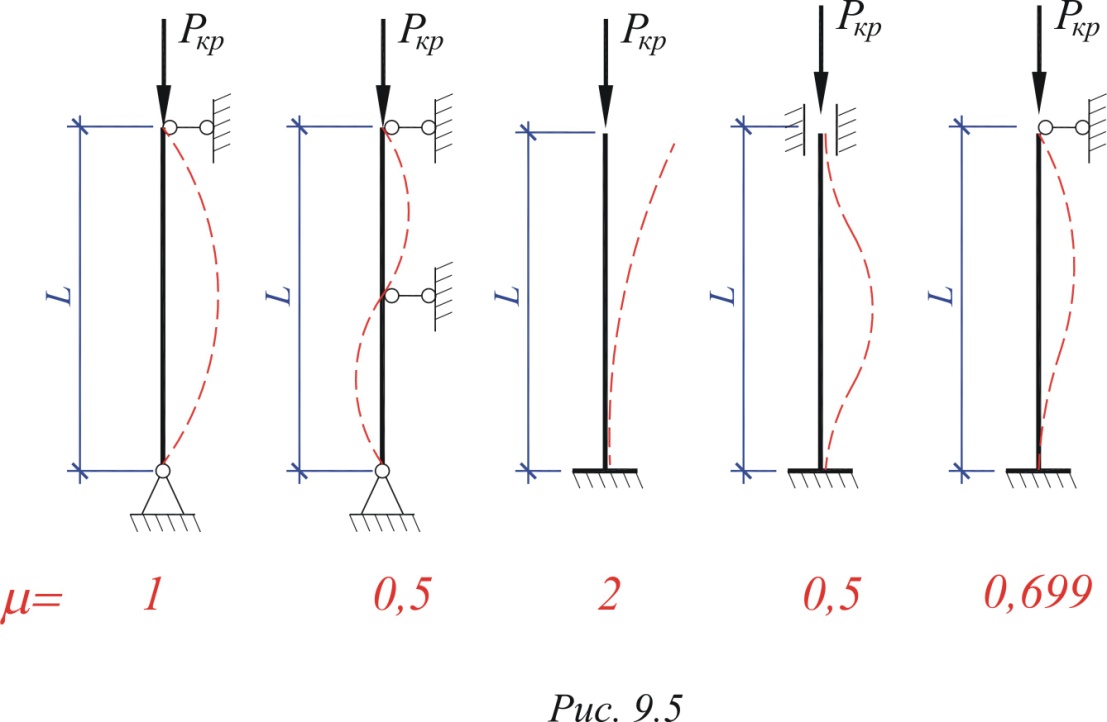
Рис.2.5.

Обобщенная формула Эйлера, учитывающая особенности закрепления стержня имеет вид:

.

(2.2)