1.3. Расчет балок на жесткость

Расчет на жесткость, о котором упоминалось в начальных лекциях нашего курса, является необходимым условием для обеспечения нормальной эксплуатации рассчитываемых конструкций. Существует целый ряд требований, которые заставляют инженеров ограничивать деформации конструкций:

• конструктивные (обеспечение целостности стыков, отделочных материалов, коммуникаций, обеспечение заданных уклонов и т.д.);

• технологические (обеспечение возможности работы технологического оборудования, корректной работы контрольно-измерительных приборов, проезда и прохода подъемно-транспортных машин и т.д.);

• физиологические (предотвращение вредных воздействий и ощущений дискомфорта при колебаниях конструкций);

• эстетико-психологические (обеспечение благоприятных впечатлений от внешнего вида конструкций, предотвращение ощущений опасности и т.д.).

Условие жесткости балочных конструкций имеет вид:

,

(1.9)

где у_max – максимальный прогиб балки, у_u – предельная величина прогиба.

Максимальная величина прогиба у_u либо задается в исходных данных задачи, либо определяется по нормативным документам в зависимости от вида рассчитываемой конструкции. В Украине для определения предельных прогибов строительных конструкций действует ДСТУ Б.В.1.2.-3:2006 «Прогибы и перемещения. Требования проектирования».

Пример 1.2.

Для консольной балки длиной L загруженной сосредоточенной силой P (рис. 1.3) подобрать поперечное сечение из двутавра и проверить условие жесткости такой конструкции. Данные принять следующие: P=13кН, L=3м, R=240МПа, E=2.0610⁶МПа. Предельную величину прогиба принять .

Максимальный по модулю изгибающий момент получаем при z=L

.

Из условия прочности при изгибе имеем:

, откуда

Принимаем двутавр 20, для которого W_x=184см³, I_x=1840см⁴.

Проверим принятое сечение на условие жесткости. Для этого необходимо определить максимальный прогиб на балке. Функция прогибов известна, необходимо ее исследовать на максимум. Приравниваем первую производную к нулю:

, - критическая точка. .

Определяем также значение функции на границах возможных значений аргумента z.

, .

Здесь важно отметить, что знак перемещения в расчетах на жесткость не важен, поскольку указывает лишь направление перемещения. Значения же перемещений принимаются по модулю. Тогда

, т.е. максимальный прогиб происходит на консоли.

Вычислим значение максимального прогиба

.

Предельная величина прогиба

.

Условие жесткости - не выполняется. Подберем новое поперечное сечения исходя из условия жесткости:

, откуда

Подбираем по сортаменту двутавр 20а с моментом инерции I_x=2030см⁴.

Лекция № 2. Понятие устойчивости, устойчивые и неустойчивые формы равновесия. Определение критической силы. Формула эйлера.

2.1. Устойчивые и неустойчивые формы равновесия. Понятие критической силы

Исследование причин разрушения различных сооружений показало, что для надежной работы конструкции под нагрузкой недостаточно сделать ее элементы прочными, необходимо еще обеспечить сохранение первоначальной формы равновесия как самих элементов, так и всей конструкции в целом.

Известно, что равновесие может быть устойчивым, безразличным и неустойчивым.

Равновесие называется устойчивым, если при малом отклонении от положения равновесия система возвращается в первоначальное положение, как только будет устранена причина, вызывающая это отклонение.

Равновесие называется неустойчивым, если система не возвращается в исходное положение, а отклоняется от него еще больше.

Равновесие называется безразличным, если новое положение системы после отклонения от исходного остается положением равновесия и после удаления внешнего воздействия.

Эти три формы равновесия можно проиллюстрировать примерами положения шарика на дне чаши, на выпуклой поверхности и на горизонтальной плоскости (рис. 2.1). В первом случае (рис. 2.1, а) шарик находится в положении устойчивого равновесия, так как при малых отклонениях он возвратится в первоначальное положение, как только будет устранена причина, вызвавшая отклонение. Во втором случае (рис. 2.1, б) исходное положение шарика может служить примером неустойчивого равновесия, а в третьем (рис. 2.1, в) – безразличного равновесия. Речь идет о малых отклонениях потому, что устойчивое равновесие при малых отклонениях может стать неустойчивым при больших отклонениях от исходного положения.

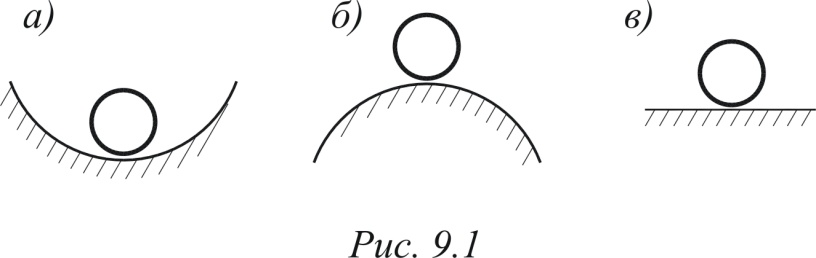
Рис.2.1.

Сказанное относится и к упругим телам. Однако характер равновесия упругих тел существенно зависит от величины действующих на них сил. Например, прямолинейная форма равновесия длинного прямого стержня, подвергнутого осевому сжатию силой Р (рис. 2.2, а), устойчива только до определенного значения сжимающей силы. Если такой стержень при малых значениях силы Р несколько отклонить от исходного положения, то при устранении причин, вызывающих это отклонение, он снова примет первоначальную прямолинейную форму.

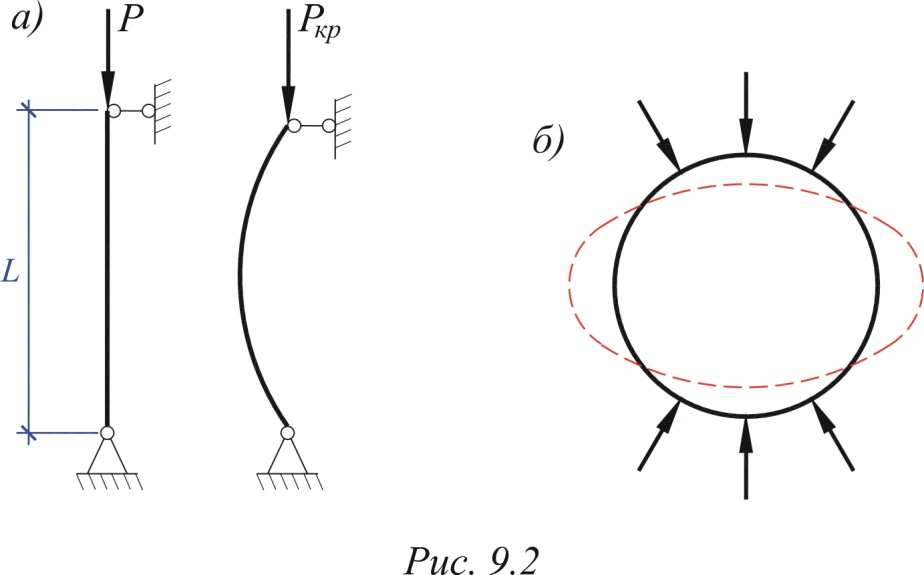
Рис.2.2.

Однако при возрастании силы Р стержень все медленнее и медленнее будет возвращаться к своей первоначальной прямолинейной форме, и, наконец, при некотором значении силы Р=Р_кр, называемом критическим, стержень не распрямится, а сохранит ту форму, которую ему придали (предполагаются малые отклонения стержня от прямолинейной формы). Таким образом, при значении силы Р, равном критическому (P=P_кр), стержень будет находиться в условиях безразличного равновесия.

Если сила Р превысит критическое значение, прямолинейная форма равновесия станет неустойчивой.

Практически изгиб стержня начинается раньше, чем сила Р достигает критического значения. Это объясняется неоднородностью материала, начальным искривлением (прогибом) оси реального стержня и некоторым эксцентриситетом в приложении нагрузки. Однако прогибы реального стержня начинают быстро расти и становятся опасными только при приближении сжимающей силы к критическому значению.

Описанное явление изгиба стержня продольной силой называется продольным изгибом.

Аналогичные явления наблюдаются в различных упругих системах, содержащих гибкие сжатые части, тонкие пластинки и оболочки. Так, например, при сжатии кругового тонкостенного кольца равномерно распределенными радиальными нагрузками происходит изменение его первоначальной круговой формы, как только интенсивность сжимающей нагрузки достигает критического значения (рис. 2.2, б).

В практических расчетах на устойчивость критическую нагрузку считают разрушающей и предельно допускаемую нагрузку P_доп определяют как часть критической:

, где

k_з – коэффициент запаса устойчивости.

Величина коэффициента запаса устойчивости принимается примерно равной запасу прочности. Например, для стальных конструкций принимают k_з=2÷4 в зависимости от условий работы конструкции, а для неоднородных материалов запас устойчивости значительно увеличивают. Также следует иметь в виду, что потеря устойчивости может произойти при напряжениях, значительно меньших допускаемых напряжений, принятых для расчета на прочность.