Лекция № 1. Перемещения при изгибе. Дифференциальное уравнение изогнутой оси балки. Расчет балок на жесткость.

1.1. Перемещения при изгибе

Изгиб балки сопровождается искривлением ее оси. При поперечном изгибе ось балки принимает вид кривой, расположенной в плоскости действия поперечных нагрузок. При этом точки оси получают поперечные смещения, а поперечные сечения совершают повороты относительно своих нейтральных осей. Различают два вида перемещений поперечных сечений в балках – прогиб y и угол поворота  (рис.1.1).

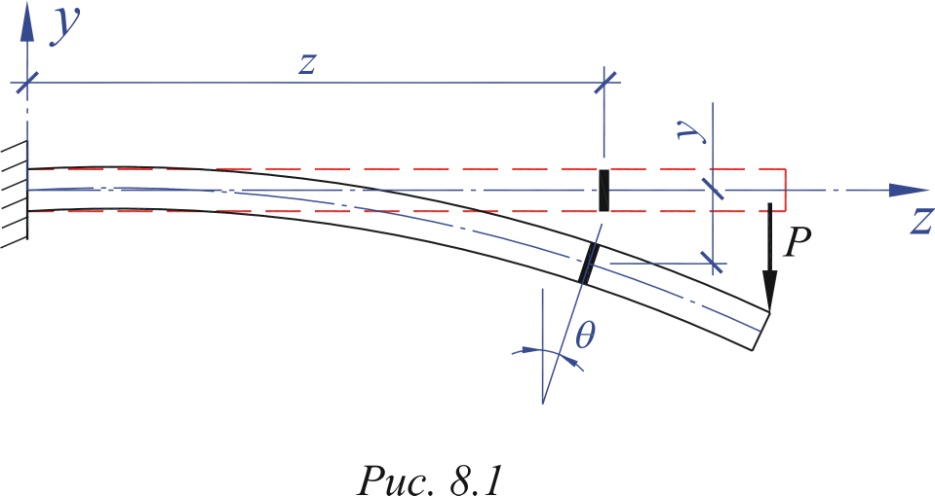
Рис.1.1.

Прогибом называется линейное перемещение центра тяжести поперечного сечения балки в направлении перпендикулярном оси балки.

Углом поворота называется угол наклона поперечного сечения к своему первоначальному положению при изгибе (поворот относительно нейтральной оси).

Прогибы и углы поворотов в балках являются функциями координаты z и их определение является задачей по вычислению перемещений.

Положительное значение прогиба y означает, что перемещение центра тяжести сечения происходит в направлении оси y принятой системы координат. Поскольку система координат в настоящем курсе принята с направлением оси y вверх, то положительный прогиб также означает перемещение вверх. Положительный угол поворота означает направление угла поворота поперечного сечения против часовой стрелки при системе координат с направлением оси z вправо (рис. 1.1). При направлении оси z влево положительный угол поворота будет по часовой стрелке. На рис. 1.1 угол поворота и прогиб выделенного сечения являются отрицательными.

1.2. Дифференциальное уравнение изогнутой оси балки

Рассмотрим плоский изгиб стержня, загруженного сосредоточенной силой Р (рис. 1.2).

На некотором расстоянии z выделим сечение (точка А), у которого будет некоторый прогиб y и угол поворота . На расстоянии dz от прежнего сечения выделим еще одно сечение (точка В) прогиб которого y+dy, а угол поворота -d. Эти два сечения образуют между собой угол d, пересекаясь в некоторой точке О. Расстояние АО=ВО=, где  - радиус кривизны балки.

Длина дуги dS, образованная этими двумя сечениями может быть найдена как:

.

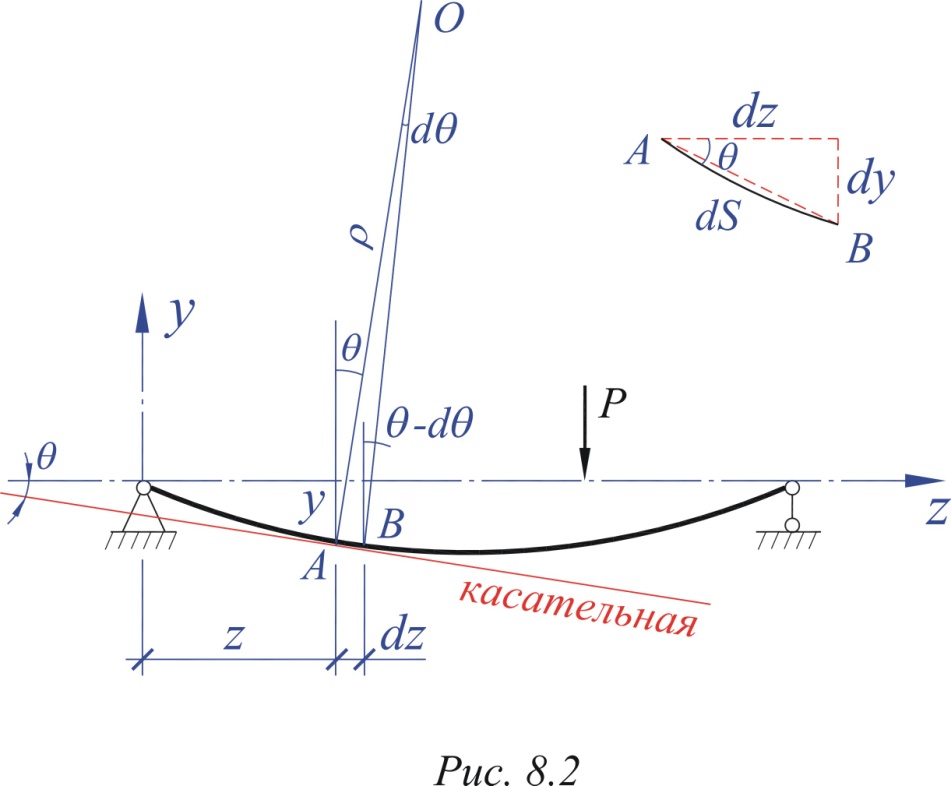
Рис.1.2.

Из элементарного треугольника (рис. 1.2), приняв АВdS, получим

, или .

Кривизна балки определится как

.

Продифференцируем угол поворота по координате

.

Используем известную тригонометрическую зависимость

.

Объединяя полученные зависимости, получим кривизну балки в виде:

.

(1.1)

Известно, что кривизна балки связана с внутренними силовыми факторами соотношением:

Приравнивая правые части уравнений, получим полное дифференциальное уравнение изогнутой оси балки:

.

(1.2)

Зачастую в инженерных расчетах угол поворота является небольшой величиной и составляет  <1…2⁰. При таких углах

, тогда
,	(1.3)

т.е. в первом приближении можно полагать, что угол поворота является первой производной от прогиба (1.1) по координате. Также проанализируем знаменатель правой части уравнения.

При рад, получим

.

Очевидно, что погрешность такого допущения не превышает 0,1%, поэтому в инженерной практике часто используют приближенное уравнение изогнутой оси бруса:

.

(1.4)

Очевидно, что уравнение является дифференциальным 2-го порядка. Интегрируя это уравнение при известной функции моментов М_x(z), можно получить функцию углов поворота и прогибов сечений балки:

,	(1.5)
.	(1.6)

Константы интегрирования С и D определяются в зависимости от граничных условий балки – условий закрепления балки на опорах.

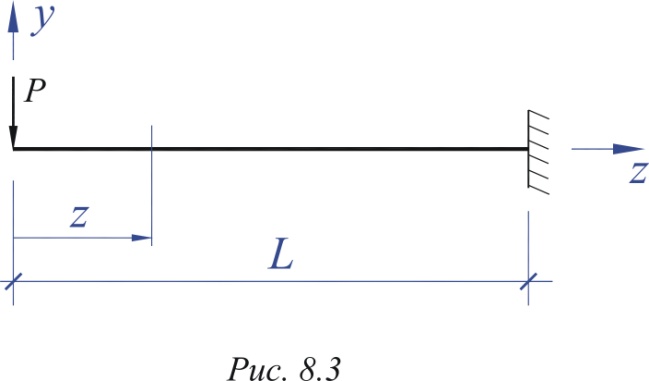
Пример 1.1. Вычислить прогиб и угол поворота на консоли длиной L при действии сосредоточенной силы P (рис. 1.3). Введем правостороннюю систему координат, совместив ее начало с левым краем балки. Выделим некоторое сечение с координатой z. Изгибающий момент в этом сечении определится как:	Рис.1.3.
.

Используем уравнение, получим

. Интегрируя по координате обе части получим
.

Константу С найдем из условия жесткого закрепления балки на опоре, т.е. . Получим

, откуда . Тогда функция углов поворота примет вид:
.	(1.7)

Интегрируя по координате еще раз, получим уравнение прогибов

.

Константу D найдем из условия жесткого закрепления балки на опоре, т.е. .

, откуда .

Тогда функция прогибов примет вид:

.

(1.8)

По условию необходимо знать прогиб и угол поворота на консоли, т.е. при z=0. Подставим z=0 в уравнения (1.7) и (1.8), получим

, .

Угол поворота сечения на консоли имеет знак «+», следовательно, поворот сечения происходит против часовой стрелки. Прогиб этого сечения имеет знак «», что означает перемещение сечения вниз.

При наличии на балке большего количества участков решение задачи усложняется, поскольку на каждом из участков уравнение моментов имеет различный вид. В этих случаях на практике используются специальные методы вычисления перемещений, например, метод начальных параметров, метод Верещагина и др. Изучение этих методов вычисления перемещений выходит за рамки настоящего курса.