8.3. Пример выполнения расчетов при действии динамических нагрузок

Рассмотрим механизм динамических расчетов на примере задачи.

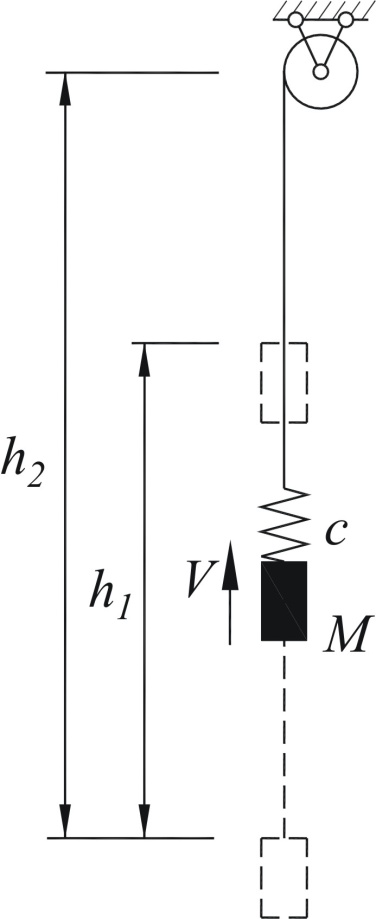
Задача 8.1. В лифтовой шахте на канате, который имеет площадь поперечного сечения нетто Fn, модуль упругости E и усилие разрыва Pp, поднимается лифт массой М на высоту h1. Лифт двигается с постоянной скоростью. Между лифтом и канатом установлена пружина с коэффициентом жесткости с. Определить максимальную скорость движения лифта из условия прочности каната при аварийной остановке лебедки, если она установлена на высоте h2 (рис. 8.2). Данные принять: Fn=47,19мм2, E=1,4105МПа, Pp=78,6кН, М=700кг, с=5105Н/г, h1=30г, h2=40г. Решение. В момент аварийной остановки система, которая двигалась с постоянной скоростью, испытывает собственные колебания со следующими начальными условиями: y0=0, V0=V. Поскольку происходят колебания только вдоль лифтовой шахты, то система имеет одну степень свободы. Уравнение движения в силу имеет вид: .

Рис. 8.2

Амплитуда собственных колебаний соответственно (8.4) равна:

.

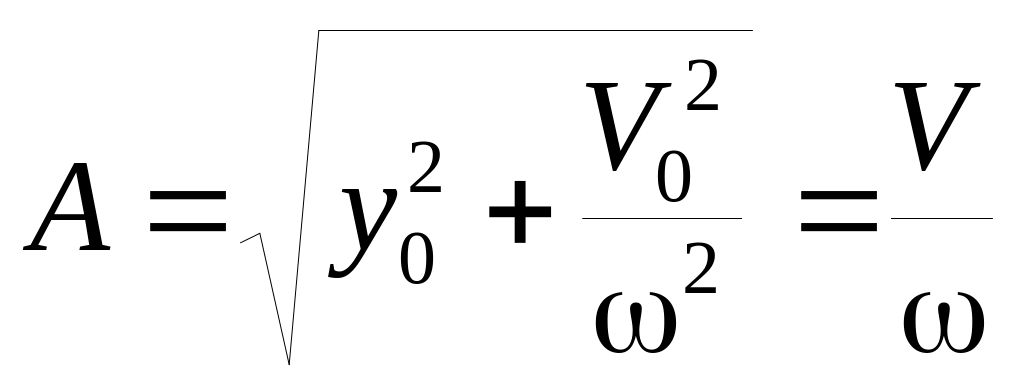Начальная фаза определится по (8.5):

,

откуда =0. Тогда уравнение движения принимает вид:

.

Находим силу инерции массы как:

Максимальная по модулю сила инерции массы возникает при :

.

Частоту собственных колебаний найдем по (8.3). Для этого найдем перемещение ₁₁ точки закрепления массы от единичной силы, приложенной в той же точке. Пусть длина каната в момент аварийной остановки составляла l. В соответствии условиям задачи . Тогда перемещение ₁₁ точки закрепления массы будет состоять из деформации троса и деформации пружины от действия единичной продольной силы:

Частота собственных колебаний равна:

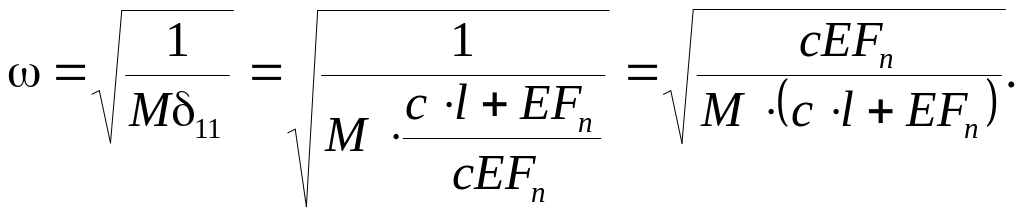
Тогда максимальная по модулю сила инерции массы равна:

.

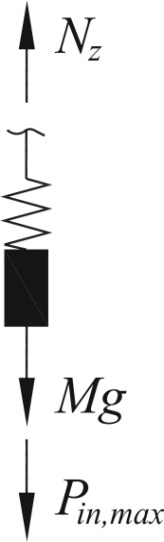
Максимальные усилия в канате возникают при совпадении направлений действия силы веса массы лифта и максимального значения силы инерции массы (рис.8.3). Из условий равновесия имеем: . По условию прочности каната внутренние усилия в канате не должны превышать усилие разрыва Pp: , тогда .

Рис. 8.3

Отсюда получим условие максимальной скорости движения:

.

Последнее выражение зависит от величины длины каната в момент аварийной остановки l. Очевидно, что правая часть неравенства принимает наименьшее значение при минимальной возможной длине каната l, т.е. при Тогда, подставив это выражение в условие максимальной скорости движения, получим выражение для вычисления максимально допустимой скорости движения лифта:

Вычислим также для данной задачи частоту собственных колебаний в расчетном состоянии, т.е. при минимально возможной длине каната :

Линейная частота колебаний связана с круговой частотой зависимостью (8.6):

Единицами измерения линейной частоты колебаний являются герцы (Гц). Линейная частота характеризует количество полных колебаний массы за промежуток времени равный одной секунде, т.е. 1 Гц=1 колебание/сек.