7.3. Статически определимые комбинированные системы

Комбинированные статически определимые системы состоят обычно из двух каких-либо жестких дисков (балочных ферм, сплошных балок, полуарок), связанных между собой промежуточным шарниром и гибкой части в виде шарнирно-стержневой системы.

а) б)

7.4. Висячие системы

Висячей называется такая система, у которой основная несущая конструкция, перекрывающая пролет, работает на растяжение. Простейшим видом висячей системы является нить (трос), перекинутая через перекрываемое пространство и несущая подвешенные к ней элементы конструкции, воспринимающие местные нагрузки.

В отличии от арочных, распор в висячих системах направлен наружу.

Лекция № 8. Основы динамики сооружений

8.1. Собственные колебания балочных систем с одной степенью свободы

Системой с одной степенью свободы называется такая система, геометрическое положение массы которой в любой момент времени определяется лишь одной координатой.

В общей теории колебаний упругих систем обычно раздельно рассматриваются системы с одной степенью свободы, а также более точные модели - с конечным и бесконечным числом степеней свободы. В случае присутствия, например, на балочных конструкциях сосредоточенных грузов с массами, которые существенным образом превышают массу самой балки, задачу приводят к системе с конечным числом степеней свободы, игнорируя при этом распределенную массу конструкции, и считая ее «невесомой» балкой.

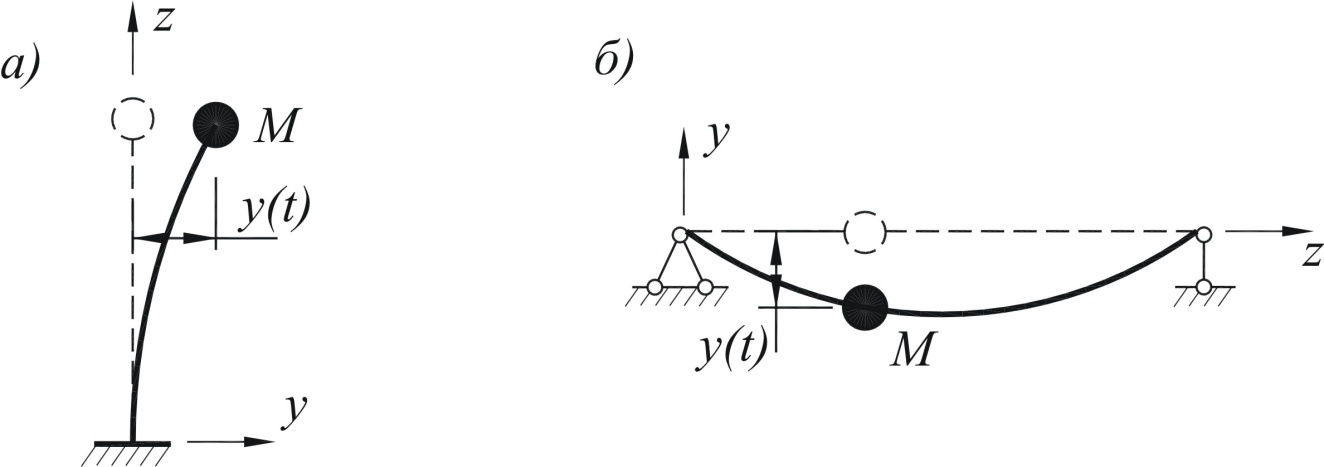
Такая система является простейшим идеализированным случаем колебательной системы (рис. 8.1).

В случае отсутствия внешней возмущающей нагрузки колебания называются свободными или собственными.

Рис. 8.1. Динамические модели с одним степенью свободы: а) невесомая консольная балка с сосредоточенной на краю массой; б) шарнирно опертая невесомая балка с сосредоточенной массой

Дифференциальное уравнение движения массы при собственных колебаниях систем с одним степенью свободы без учета сил сопротивления движения имеет вид:

.

(8.1)

Решение этого уравнения можно представить в виде:

,

(8.2)

где А,  и  – соответственно амплитуда, круговая (угловая) частота и начальная фаза колебаний.

Собственные колебания возникают при задании системе некоторых начальных возмущающих параметров – начального перемещения y₀ и начальной скорости V₀. При этом характеристики процесса колебаний определятся как:

,	(8.3)
,	(8.4)
,	(8.5)

где g – ускорение свободного падения (g=9,81 м/с²).

Очевидно, что для использования этих формул необходимо знать величину ₁₁ – прогиба балки в точке закрепления массы от единичной силы, приложенной в той же точке, или такой же прогиб балки f вычислен от действия силы веса груза – f=₁₁Mg.

Линейная частота колебаний связана с круговой частотой колебаний зависимостью:

.

(8.6)

Имея закон перемещения массы во времени (8.2), можно найти силу инерции массы при колебаниях . Сила инерции массы является динамической нагрузкой, на действие которой совместно со статической нагрузкой осуществляется расчет конструкций на прочность и жесткость.