Изгибающие моменты в сечениях арок
Определим М в сечении I-I
- момент в сечении простой балки, расположенном под сечением арки, причем балка имеет тот же пролет и ту же нагрузку, что и арка.
Тогда изгибающий момент в любом сечении балки определяется
М
х
=
–
H·y
(7.1)
Из выражения (1) следует, что моменты в сечениях арки меньше моментов в соответствующих сечениях балки, следовательно, арка экономичнее балки и аркой можно перекрыть пролет гораздо больше, чем балкой.
Для определенного вида нагрузки можно подобрать такое очертание оси арки, что изгибающий момент М в любом сечении арки будет равен нулю. Такие арки называются арками с рациональным очертанием оси.
У
равнение
оси арки рационального очертания.
Пример.
Пусть трехшарнирная арка загружена равномерно распределенной нагрузкой по всему пролету.
Тогда 
- уравнение
квадратной
параболы.
Поперечные и продольные силы в сечениях арок
Определим поперечную и продольную силу в сечении I-I арки.
Поперечная сила Q в сечении арки равна сумме проекций всех сил, расположенных по одну сторону от сечения на нормаль к касательной, проведенной к оси арки в рассматриваемом сечении.
Q0Х
-
балочная поперечная сила. Тогда можно
записать
(7.2)
Поперечная сила в арке меньше поперечной силы в сечениях простой балки.
Продольная сила N в сечении арки равна сумме проекций всех сил, расположенных по одну сторону от сечения, на касательную к оси арки, проведенную в данном сечении.
(7.3)
Выводы:
1) преимуществом арки перед балкой является уменьшение величин M и Q в сечениях арки;
2) недостатками арки являются:
а) появление значительных продольных сил в сечениях;
б) необходимость восприятия распора, что требует устройства более могучих опор.
Построение эпюр m, q, n в арках.
Для построения эпюр пролет арки разбивается на несколько равных частей (10-15) и в каждом сечении, в соответствии с выражениями (7.1), (7.2), (7.3) определяют значения Mx, Qx, Nx и по этим значениям строят эпюры.
Расчет обычно сводят в таблицу.
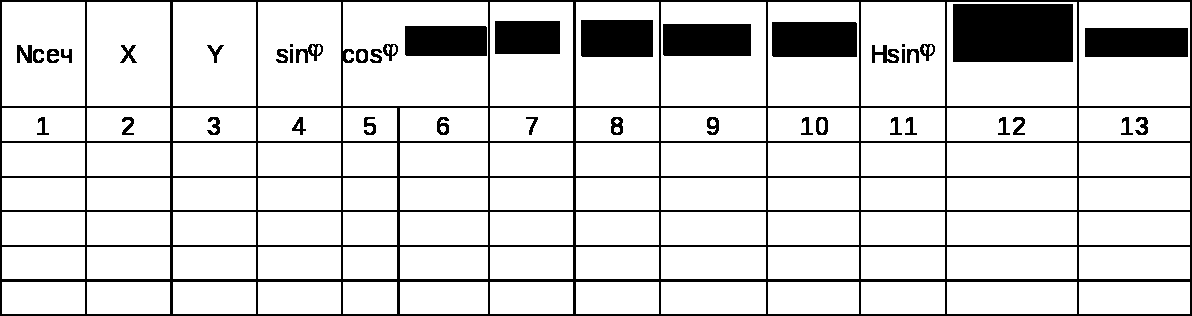
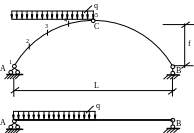
y=f(x) 
Эпюры
Q и N криволинейны, т.к. в формулы (2) и (3)
входят sin
и cos
.
На эпюре Q в точке приложения сосредоточенной силы должен быть скачок на величину P;cos , а на эпюре N - на P;sin .
Расчет трехшарнирных арок с затяжками.
В таких арках распор воспринимается затяжкой.
Опорные реакции определяются:
1)
2)
Для определения усилия в затяжке, проводят сечение через затяжку и шарнир С и составляют одно из уравнений:
или 
откуда определяют Hз.
Усилия в сечениях арки с затяжкой определяются по формулам (1) - (3), только вместо распора Н принимают Нз.
М
х
= Мх
- Нзy
Qx = cos - Hзsin
Nx = - sin - Hзcos