Лекция № 7. Трехшарнирные системы

Трехшарнирная система состоит из двух дисков, соединенных между собой шарниром (С) и прикрепленных шарнирами (А и В) к земле.

1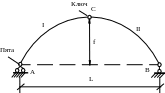 ) 2)

Если диски I и II представляют собой криволинейные брусья, то такая система называется трехшарнирной аркой. Если дисками I и II являются ломаные стержни, то система называется трехшарнирной рамой.

Шарниры А и В называются опорными или пятовыми шарнирами, С - ключевой шарнир.

Расстояние между опорными шарнирами АВ по горизонтали называется пролетом арки или рамы. Расстояние от ключа до линии, соединяющей опорные шарниры, называется стрелой подъема арки f.

Если - пологие арки

- повышенные арки

Трехшарнирные системы являются статически определимыми системами, так как :

W = 3D - 2Ш₀ - С_оп = 3·2 - 2·1 - 4 = 0

и геометрически неизменяемыми.

Трехшарнирные системы - это распорные системы, так как в их опорах, даже при отсутствии вертикальной нагрузки, возникают горизонтальные составляющие опорных реакций.

Для определения опорных реакций мы можем составить три уравнения статики, а наличие ключевого шарнира С позволяет составить дополнительное уравнение:

или

и определить все четыре опорные реакции.

Трехшарнирные системы могут быть симметричными и несимметричными

3 )

Опорные шарниры А и В могут располагаться в одном уровне (рис.3) и могут располагаться в разных уровнях (4) - такие системы называются ползучими арками или рамами.

4 )

В практике часто встречаются системы, у которых распор воспринимается затяжкой:

5) 6)

арка с затяжкой арка с повышенной затяжкой

Если каждая полуарка выполнена в виде фермы, то такая система называется сквозной аркой или трехшарнирной фермой.

6)

7.1. Сплошные трехшарнирные арки. Определение опорных реакций.

При действии на арку внешней нагрузки, в каждой ее опоре возникают по две реакции: горизонтальная и вертикальная.

Для определения всех опорных реакций мы можем записать для плоской системы три уравнения статики и для трехшарнирной арки можно составить четвертое уравнение, приравняв к нулю сумму моментов правых либо левых сил относительно шарнира С.

Следовательно реакции определяются:

1)

2)

Глядя на полученные выше уравнения, можно сделать вывод, что вертикальные составляющие опорных реакций трехшарнирных систем, равны балочным.

3)

4) H_A = H_B;

Если на трехшарнирную арку действует только вертикальная нагрузка, то распоры равны между собой

H_A = H_B = H

Чем больше стрела подъема арки, тем меньше распор.

7.2. Определение внутренних усилий в сечениях трехшарнирной арки

Внутренними усилиями, возникающими в поперечных стержнях арки, являются изгибающие моменты М, поперечные силы Q и продольные силы N.

П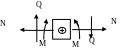 равило знаков