6.2. Статическая определимость и геометрическая неизменяемость рам

Как и любая расчетная схема строительного сооружения рама должна представлять собой геометрически неизменяемую систему. Правила проверки геометрической неизменяемости систем рассмотрены ранее, поэтому лишь напомним, что количество степеней свободы W можно определить по формуле Чебышева:

,

где W – количество степеней свободы системы, D – количество дисков в системе, Ш – количество простых шарниров (шарниры внешних связей не учитываются), С₀ – количество внешних связей. Для геометрически неизменяемых систем обязательным условием является W  0. Однако окончательный вывод о геометрической неизменяемости систем делаю с помощью кинематического анализа, который также рассмотрен в предыдущих лекциях.

6.3. Определение опорных реакций и построение эпюр внутренних силовых факторов

Для определения опорных реакций в статически определимых рамах достаточно использовать условия равновесия тела. При этом, также как и для определения опорных реакций в балках, уравнения пытаются составить так, чтобы в каждом из них было не более одной неизвестной. Это позволит облегчить процесс решения задачи, избегая решения систем уравнений.

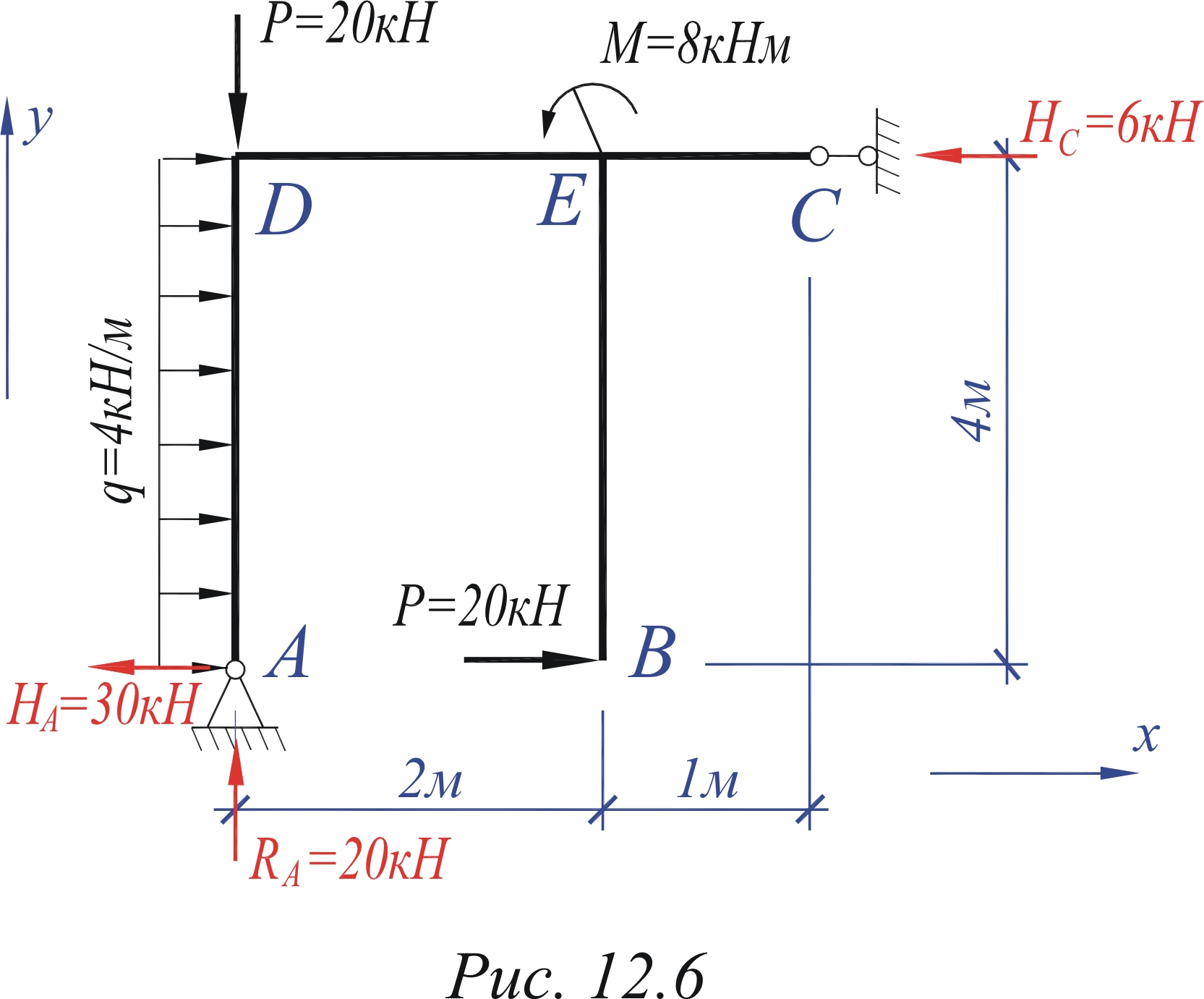
Рассмотрим раму на рис. 6.4 и определим опорные реакции в этой раме. Опоры рамы находятся в точках А и С. Отбрасываем связи, заменяя их силами опорных реакций. В точке А расположена шарнирно неподвижная опора, которую заменяем на две силы реакции R_A и H_A. В точке С расположена шарнирно подвижная опора, которую заменяем на реакцию Hс. Направление опорных реакций изначально выбирается произвольно. Анализируем уравнения

проекций сил на оси x и y: – содержит две неизвестных реакции, оставим данное уравнение для проверки; , откуда . В качестве моментной точки для уравнения равновесия моментов выбираем такую точку, которая позволит исключить из уравнения две неизвестные реакции из трех. Эти точки располагаются на пересечении опорных реакций, т.е. т. А и т. D. Составим эти уравнения: ;

Рис.6.4.

, откуда

.

, откуда

.

Наносим полученные значения реакций на расчетную схему и корректируем при необходимости начальное направление реакций. Напоминаем, что для реакций, полученных со знаком минус, следует изменить исходное направление на противоположное, а само значение записать положительным.

Проверяем правильность найденных реакций. Для этого используем уравнение:

.

Для построения эпюр в рамах необходимо знать, что вследствие произвольного расположения стержней рамы и нагрузок, в общем случае в поперечном сечении элементов рамы возникают: изгибающие моменты, поперечные силы и продольные силы. Построение эпюр можно разделить на отдельные этапы:

1) Раму разбивают на участки. Участками рамы называются части рамы, между точками приложения сосредоточенных нагрузок, точками начала или окончания распределенной нагрузки и точками узлов рамы.

2) На каждом участке производят рассечение рамы на две части, одну из которых рассматривают в равновесии. При этом удобно расположить отсеченную часть рамы так, чтобы она заняла горизонтальное положение, и применить при этом все правила построения эпюр поперечных сил, изгибающих моментов и продольных сил для этого участка балки. Построение эпюр продольных сил в некотором роде было рассмотрено ранее. Дадим определение продольной силы в сечении.

Продольной силой называется равнодействующая потока нормальных усилий в поперечном сечении. Продольная сила равна сумме проекций всех внешних сил, расположенных по одну сторону от сечения, на продольную ось стержня, и взятых с определенным знаком.

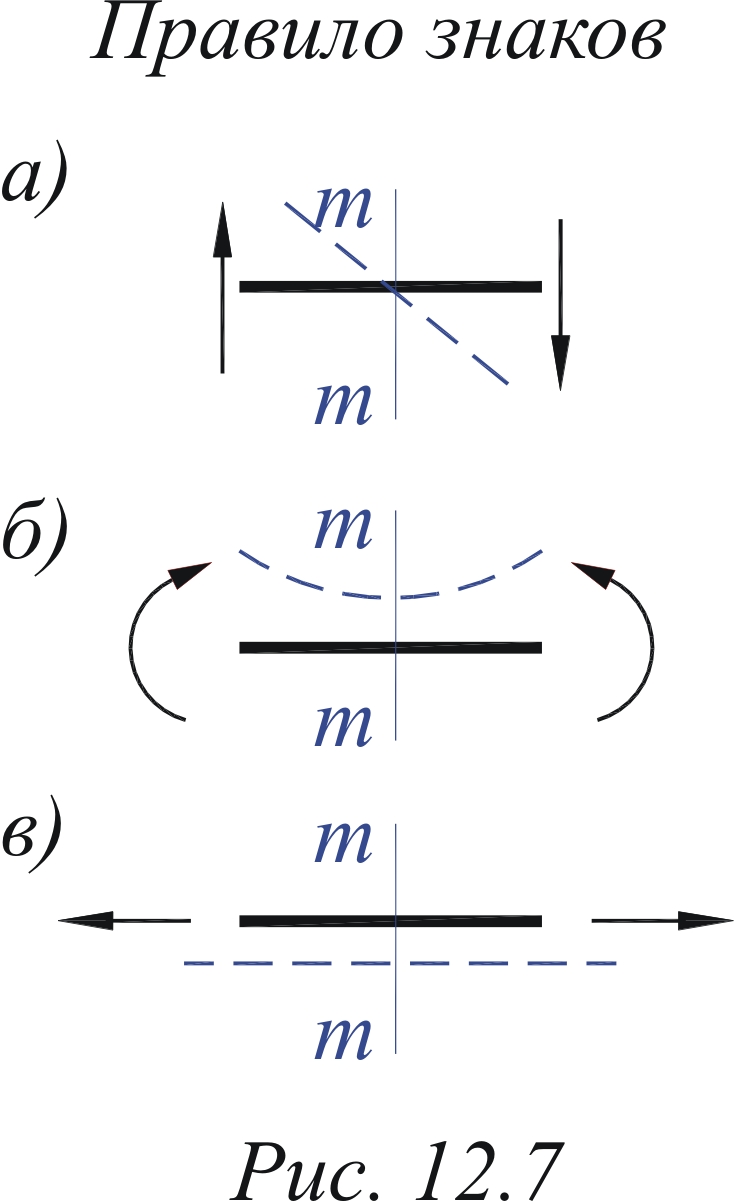
Продольная сила является положительной, если она вызывает растяжение стержня (6.5, в). Таким образом, правило знаков, которое было использовано для записи налитических уравнений в балках для поперечной силы (рис. 6.5, а) и для изгибающего момента (рис. 6.5, б), можно дополнить правилом для продольной силы (рис. 6.5, в). Записывают аналитические выражения для внутренних силовых факторов на каждом участке. Рекомендуется также изобразить эпюру изгибающих моментов, а при необходимости и эпюру поперечных сил, для данного участка как для отдельной балки по всем известным правилам построения эпюр в балках.

Рис.6.5.

3) По аналитическим зависимостям строят эпюры в раме. При этом положительные значения ординат эпюры откладывают в раме, как правило, сверху на ригелях и слева на стойках. На эпюрах поперечных и продольных сил указывают знак, на эпюрах изгибающих моментов знак не указывают, а эпюру строят на растянутых волокнах. Проще всего определить расположение растянутых волокон по уже построенной эпюре изгибающих моментов для данного участка как для балки. Для этого рекомендуется замаркировать соответствующие точки эпюры в раме и эпюры в балке, а затем совместить их, убирая знак.

Штриховка всех эпюр в рамах осуществляется линиями перпендикулярными осям стержней рамы.

4) После построения эпюр в рамах выполняют проверку равновесия узлов. Суть проверки заключается в том, что из рамы вырезают узел, в соответствии с эпюрами указывают направление и величину внутренних усилий и проверяют выполнение условий равновесия тела.

Построим эпюры на примере рамы на рис. 6.6.

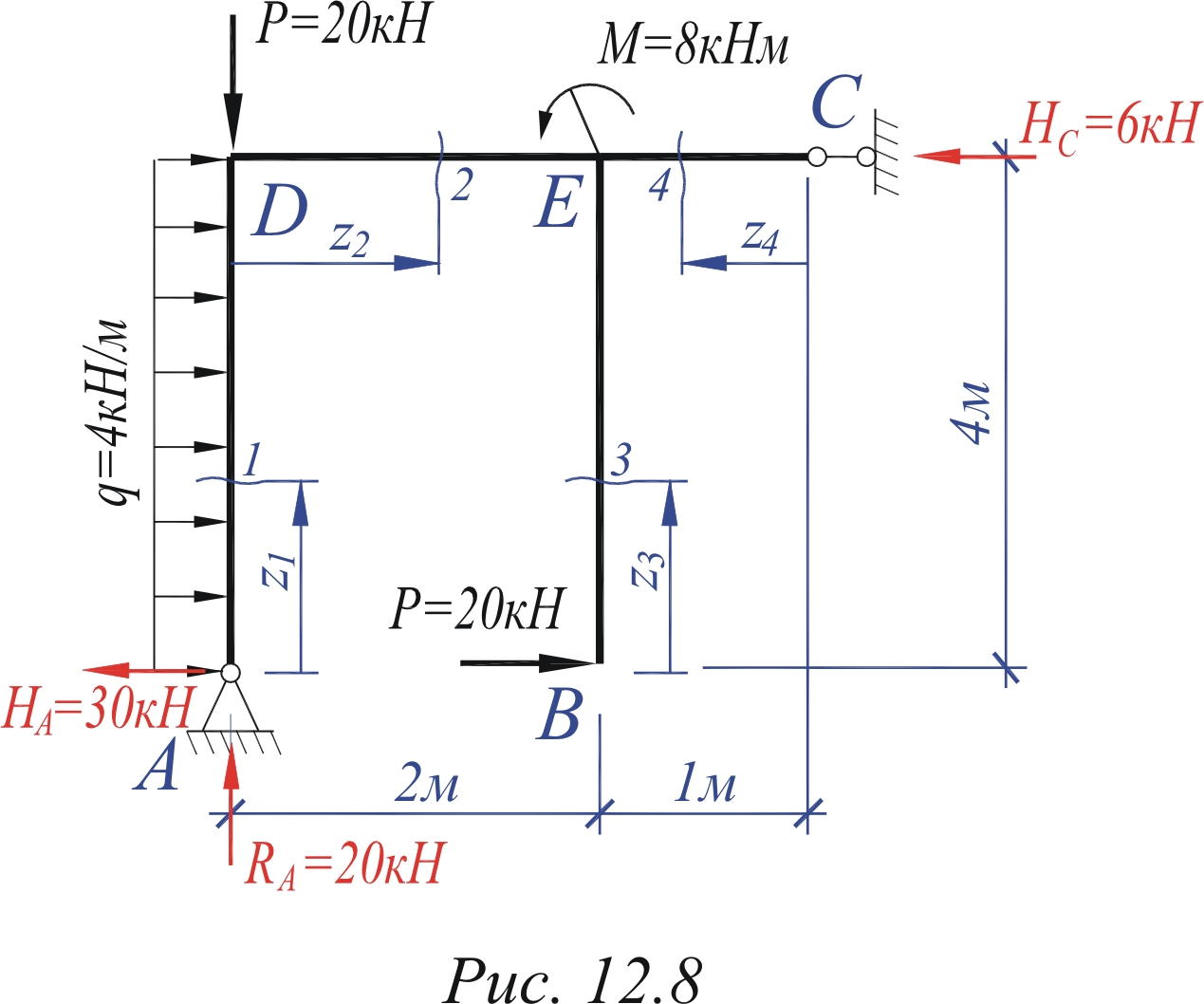
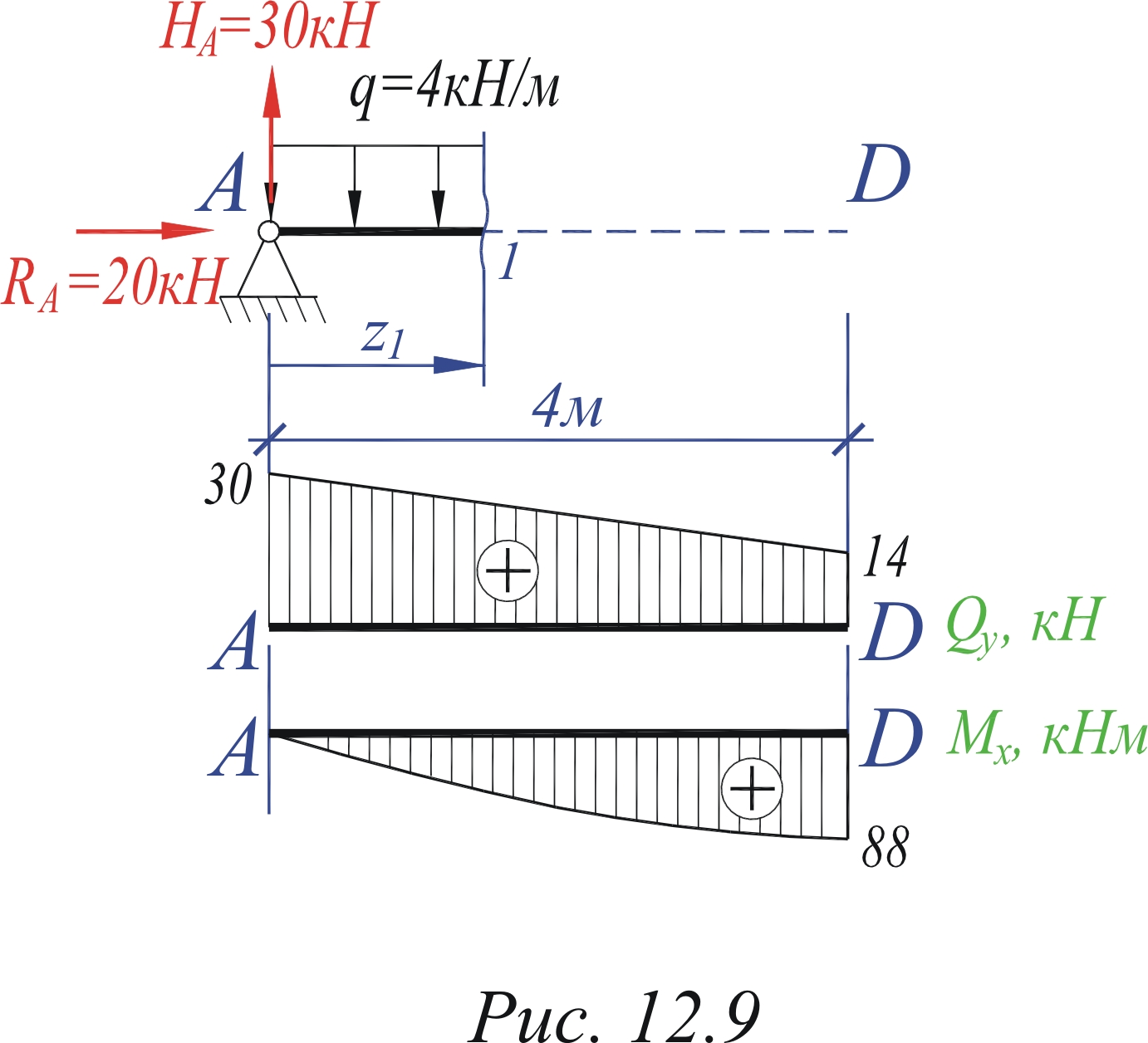
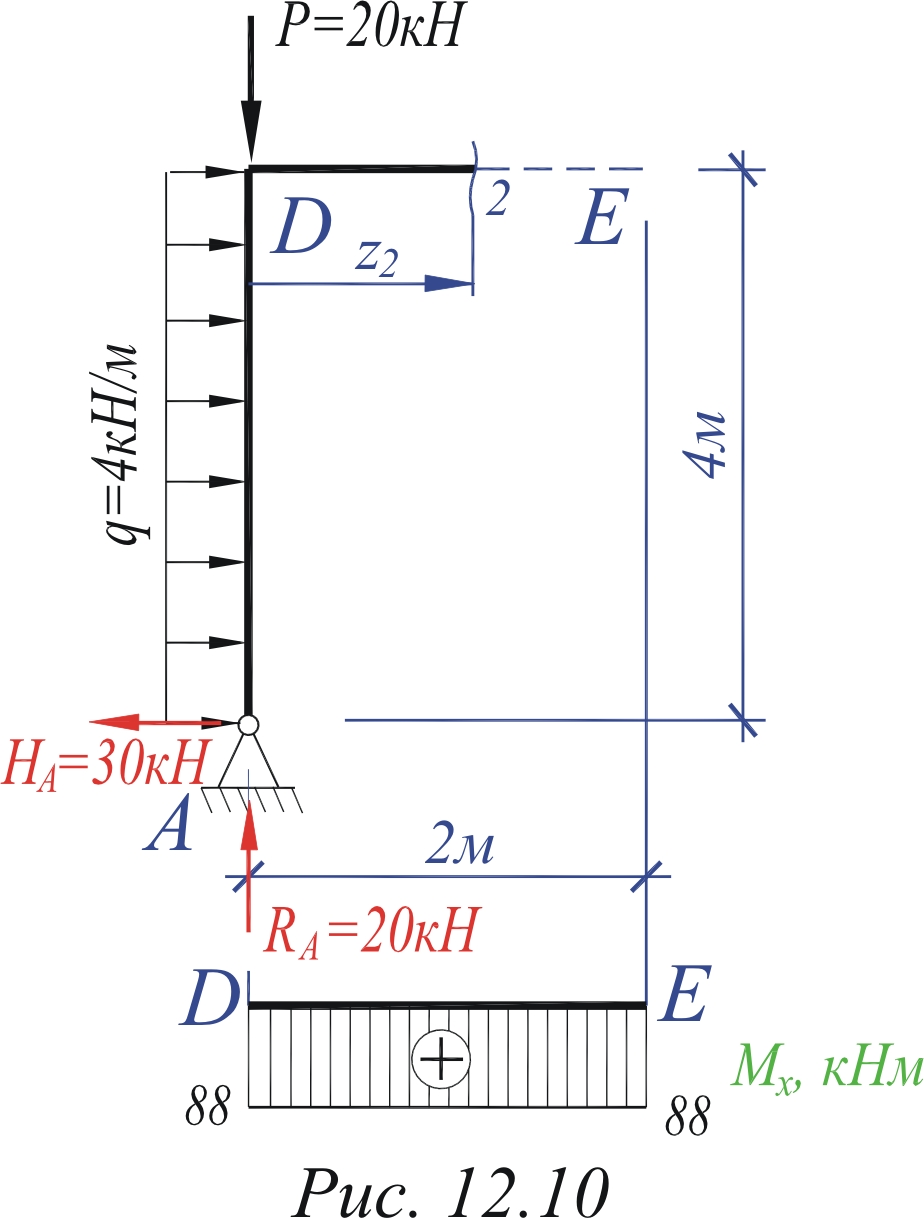
Разбиваем данную раму на участки. Получаем четыре участка: A-D, D-E, B-E, C-E. На каждом из них проводим сечение, разбивая раму на две части, и вводим "плавающую" систему координат. Напоминаем, что начало "плавающей" системы координат совпадает с границей участка, которая оказалась на выбранной отсеченной части рамы. Рассмотрим отсеченную часть рамы сечением 1 на первом участке – A–D, и изобразим её отдельно так, чтобы рассеченный стержень занял горизонтальное положение (рис. 6.7). Участок 1 0≤z1≤4м. Qy=НA – qz1=30 – 4 z1; Qy(0)=30 (кН); Qy(4)=14 (кН). ; Mx(0)=0; Mx(4)=88 (кНм). Nz= –RA= –20 (кН). Строим эпюры Qy и Mx для стержня A–D как для балки (эпюра Qy нужна для правильного построения эпюры Mx). Обозначаем точки границ участка на эпюрах и переносим полученные эпюры на раму, убирая при этом с эпюры моментов знак (рис. 6.7, а, б). Эпюру Nz строим сразу на раме (рис. 6.13, в). Рассмотрим отсеченную часть рамы сечением 2 на втором участке – D–Е, и изобразим её отдельно так, чтобы рассеченный стержень занял горизонтальное положение (рис. 6.8). Участок 2 0≤z2≤2м. Qy=RA –P =20 – 20=0. 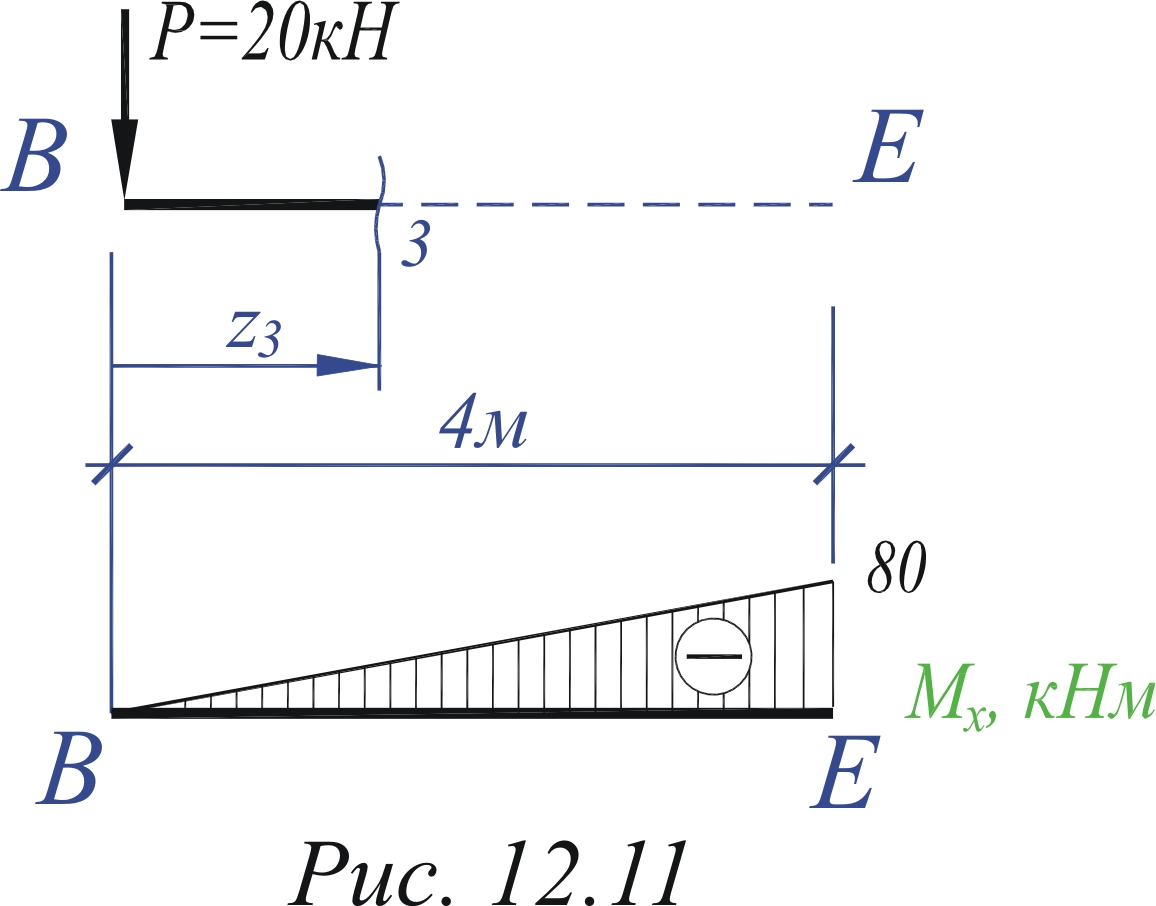=120 – 32 + 20z2 – 20z2 = 88 (кНм). Nz= HA – q4= 30 – 16 =14 (кН). Эпюру моментов изображаем сначала на стержне D–Е как на балке, а затем переносим на раму, убирая знак (рис. 6.8, б). Остальные эпюры строим сразу на раме (рис. 6.11, а, в). Рассмотрим отсеченную часть рамы сечением 3 на втором участке – В–Е, и изобразим её отдельно так, чтобы рассеченный стержень занял горизонтальное положение (рис. 6.9). Участок 3 0≤z3≤4м. Qy=–P = – 20 (кН). 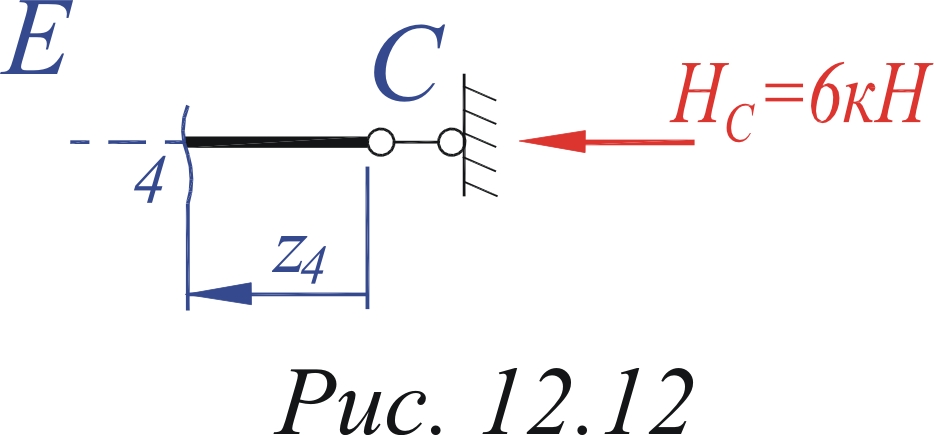; Mx(0) = 0; Mx(4)= – 204 = -80 (кНм). Nz= 0. Эпюру моментов изображаем сначала на стержне В–Е как на балке, а затем переносим на раму, убирая знак (рис. 6.11, б). Остальные эпюры строим сразу на раме (рис. 6.11, а, в). Рассмотрим отсеченную часть рамы сечением 3 на втором участке – С–Е, и изобразим её отдельно так, чтобы рассеченный стержень занял горизонтальное положение (рис. 6.10). Участок 4 0≤z4≤1м. Qy=0. Mx = 0. Nz = – Hc = – 6 (кН). Все эпюры стром на раме (рис. 6.11, а, б, в).

Рис.6.6. Рис.6.7. Рис.6.8. Рис.6.9. Рис.6.10.

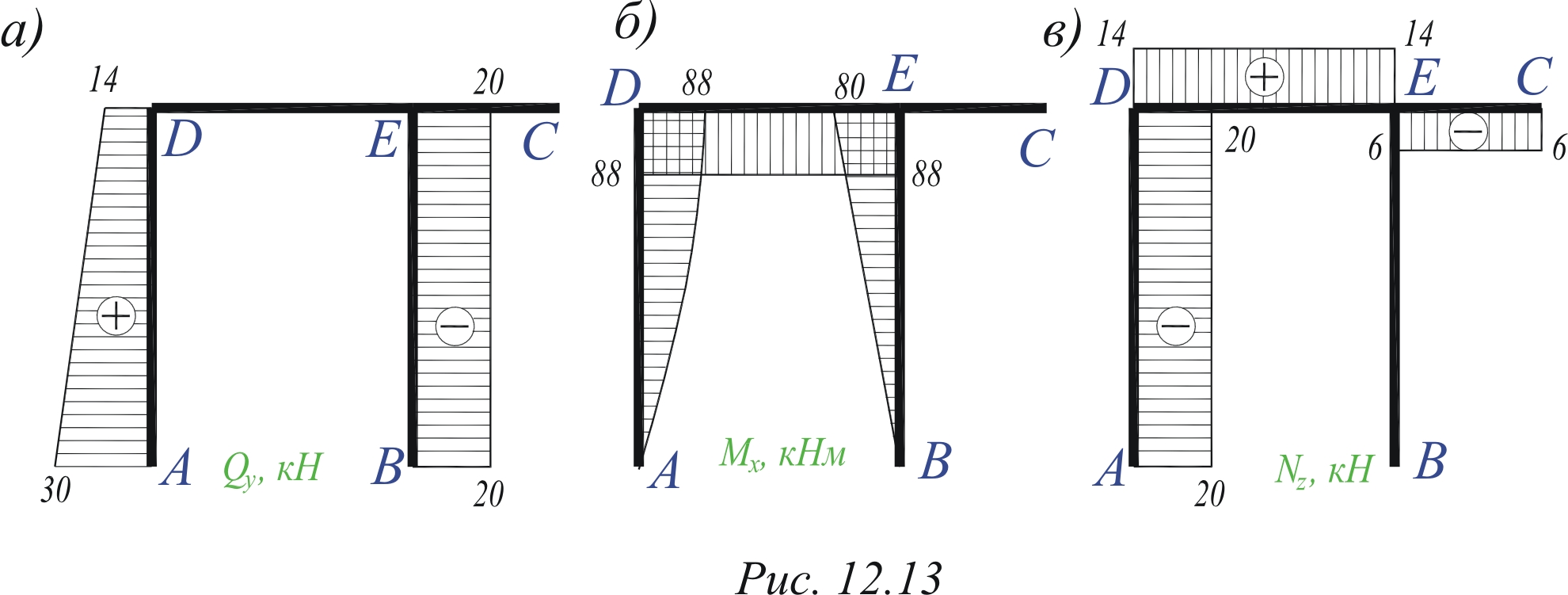
Рис.6.11.

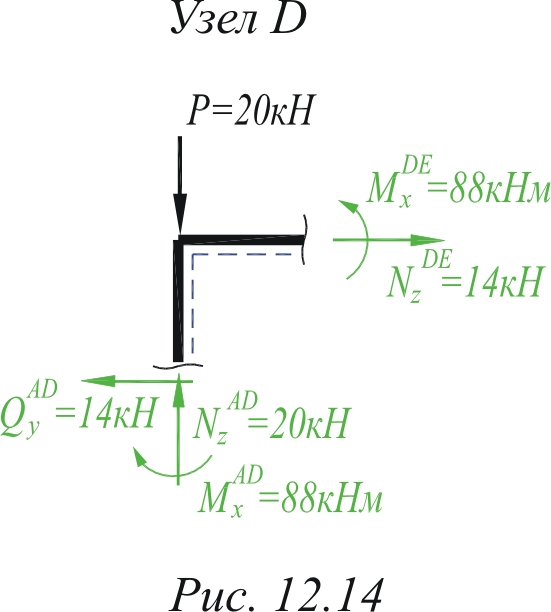
После построения эпюр выполняют проверку равновесия узлов рамы. Для этого из рамы вырезают узел сечениями, проходящими бесконечно близко к узлу, и изображают его отдельно с указанием внутренних усилий в местах рассечения. Рассмотрим проверку равновесия узла на примере узла D рамы (рис. 6.12). Вырезаем данный узел из рамы и прикладываем внешние нагрузки, оставшиеся на отсеченном узле. Поскольку сечение проходят бесконечно близко к узлу, то такие нагрузки могут быть только узловые (напомним, что распределенная сила характеризуется длиной приложения, которая в данном случае будет бесконечно малой). В узле D на исходной схеме приложена сосредоточенная сила P, которая очевидно и останется на отсеченном узле. В местах рассечения вместо отброшенной части рамы указываем внутренние усилия. Значения внутренних усилий в сечениях берем с соответствующих эпюр (рис. 6.11). Направление усилий назначаем с учетом знака. Проще всего рассуждать так: закрепим мысленно рассматриваемый узел в точке D. Тогда положительная продольная сила, должна растягивать

стержни, а положительная поперечная сила вращать узел по часовой стрелке. Для определения правильного направления момента рекомендуется пометить пунктиром растянутые волокна стержня. Для этого нужно определить, с какой стороны на стержне изображена эпюра моментов в данном сечении рамы. Поскольку эпюра моментов строится на растянутых волокнах, то эту сторону стержня и следует пометить пунктиром. Дальше направляем момент так, чтобы он растягивал помеченные волокна, т.е. "хвост" момента со стороны растянутых волокон (иногда говорят "хвост момента со стороны эпюры"). После указания всех внутренних усилий составляют уравнения равновесия тела:

Рис.6.12.

Узел D находится в равновесии. Отметим, что полученная система сил на рис. 6.12 – сходящаяся, поэтому в последнем уравнении данной системы важно проверить равновесие только моментов пар сил (сосредоточенных моментов). В этом случае моментная точка может быть любой и может вообще не указываться.

Аналогично проверяем равновесие узла Е (рис. 6.13).

Узел Е находится в равновесии.

Рис.6.13.