4.1. Классификация ферм.

Фермы можно классифицировать по различным признакам, а именно:

1) По материалу, различают фермы металлические, стальные, деревянные, металлодеревянные, железобетонные.

2) По направлению опорных реакций:

а) безраспорные фермы, которые могут быть:

балочные фермы

к онсольные фермы

консольно-балочные фермы

б) распорные фермы, в опорах которых даже при вертикальной нагрузке возникают как вертикальные, так и горизонтальные опорные реакции, например :

а рочные - распор у которых направлен внутрь

висячие - распор у которых направлен наружу.

3) По очертанию поясов. С этой точки зрения фермы могут быть следующие:

а) фермы с параллельными поясами

б) фермы полигонального (ломанного) очертания

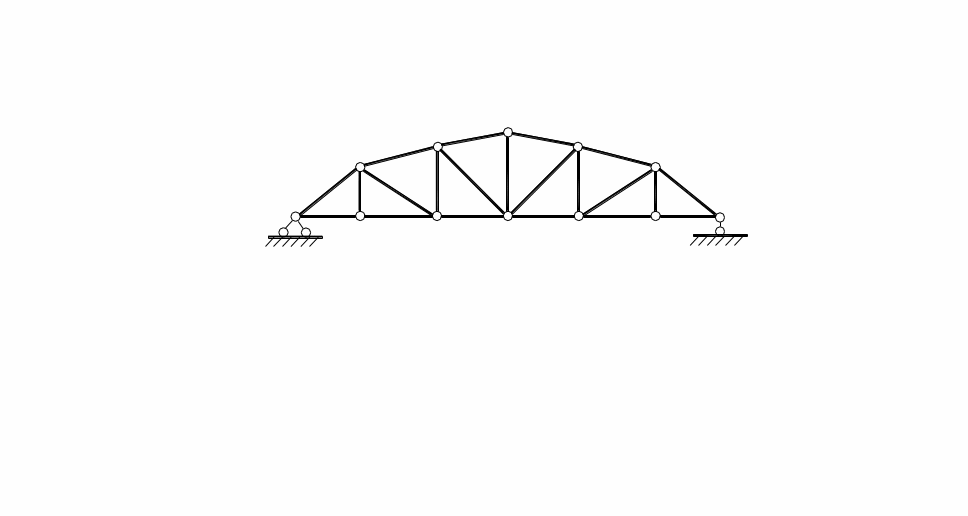
в) треугольные фермы

г) фермы криволинейного очертания - узлы верхнего или нижнего пояса, или обоих поясов, располагаются по кривой, однако сами стержни обязательно прямые

4) По типу решетки:

а) с раскосной решеткой - фермы, у которых решетка состоит из раскосов и стоек. В зависимости от направления раскосов различают решетки с нисходящими и восходящими раскосами

с нисходящими раскосами с восходящими раскосами

б) фермы с треугольной решеткой

в) полураскосные фермы - у них раскосы идут не от пояса к поясу, а от поясов к середине стоек

Рассмотренные выше типы решеток являются простыми решетками, однако часто применяются и сложные решетки:

г) многораскосные фермы - их решетка состоит из нескольких раскосных решеток, наложенных друг на друга

д) шпренгельные фермы - у таких ферм дополнительно к основным стержням решетки вводятся новые стержни, которые делят панели поясов на части, благодаря чему удается избежать внеузлового загружения ферм

е) составные фермы - это фермы, у которых отдельные стержни заменены сложными системами, в свою очередь представляющие собой фермы.

4.2. Расчет статически определимых плоских ферм.

Конечной целью статического расчета фермы является определение усилий в ее стержнях. По этим усилиям в дальнейшем производят подбор сечений элементов фермы и расчет узловых прикреплений элементов (расчет заклепок, сварных швов, врубок, болтов, шпонок).

Для расчета ферм разработан ряд методов, которые можно разделить на две основные группы: статические и динамические. Основой всех статических методов расчета является, способ сечений, который состоит в следующем: из фермы вырезают отдельные узлы, или целые области, или рассекают ферму на две части, после чего для рассматриваемого участка фермы составляется одно из уравнений статики, содержащее в себе одно неизвестное усилие.

Вместе с тем, каждый из статических способов имеет свои особенности, которые и рассмотрим.

Способ вырезания узлов

Сущность этого способа состоит в следующем: из фермы, начиная с узла, где сходятся не более двух стержней с неизвестными усилиями, последовательно вырезают узлы вместе с приложенными к ним нагрузками (в том числе и опорными реакциями). Рассматривая равновесие узла, мы имеем дело с системой сходящихся, для которой можно составить только два уравнения статики:

из решения которых и определяют усилия в стержнях.

Поэтому и каждый последующий вырезанный узел может содержать любое количество стержней, но неизвестными должны быть усилия только в двух стержнях.

Примечание:

Вырезав узел, усилия направляют вдоль осей стержней от узла, считая стержни растянутыми. Если результат получится со знаком "-", то это значит, что стержень сжат.

Оценка способа. Его выгодно применять для расчета ферм простейшего очертания, с небольшим количеством узлов в том случае, когда нужно определить усилие во всех стержнях фермы.

П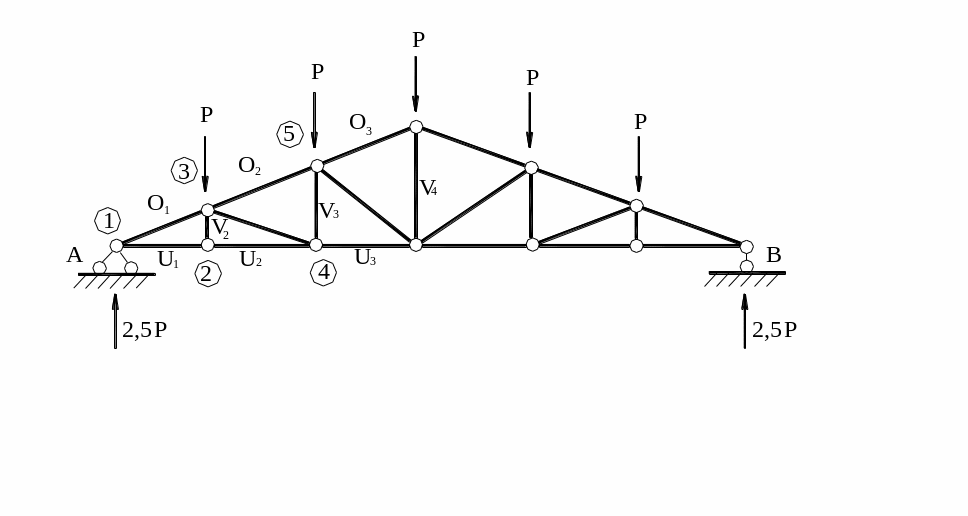 ример:

Решение:

1. Определяем реакции опор

2) Намечаем порядок последовательного вырезания узлов фермы, начиная с узла, где сходятся два стержня.

3. Каждый узел вычерчиваем отдельно, составляем и решаем уравнения статики.

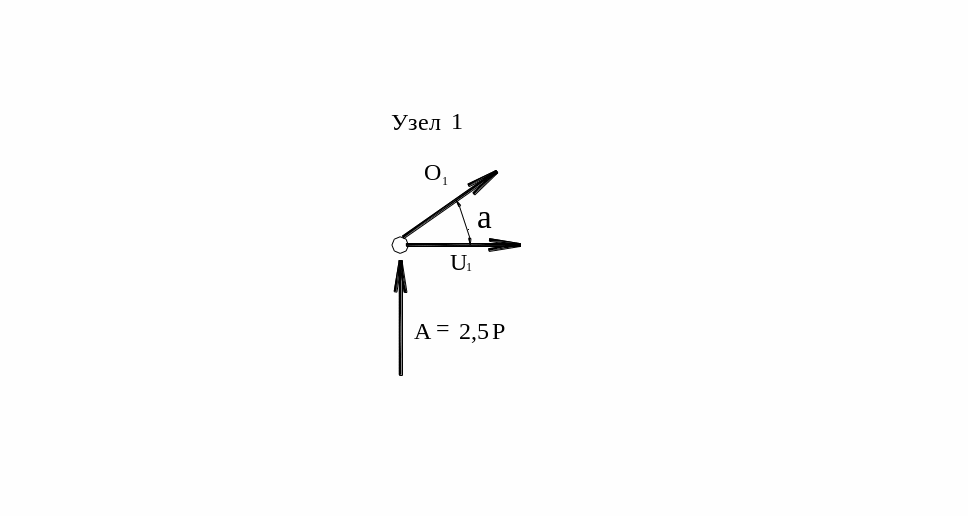
Частные случаи способа узловых вырезов.

П равило 1.

Если в узле фермы сходятся два стержня (под любым углом) и никакой нагрузки к узлу не приложено, то оба стержня будут "нулевые".

Доказательство:

, но так как

П равило 2.

Если в двухстержневом узле по направлению одного из стержней действует сила Р, то усилие в том стержне равно самой силе, но имеет противоположное направление, а второй стержень будет "нулевым".

Доказательство:

П равило 3.

В узле сходятся три стержня, два из которых лежат на одной прямой, а третий примыкает к ним под любым углом. Если узловой нагрузки нет, то усилия в двух первых стержнях будут одинаковыми, как по величине, так и по знаку, а третий стержень будет "нулевым".

Доказательство:

Правило 4.

Если в узле сходится три стержня, два из которых направлены по о дной прямой , а по направлению третьего стержня действует сила Р, то усилие в третьем стержне будет равно самой нагрузке, но иметь противоположное направление, а в первых двух стержнях усилия будут одинаковые как по величине, так и по знаку.

Доказательство:

П равило 5.

Если в узле сходятся четыре стержня попарно лежащие на двух прямых и никакой нагрузки в узле нет, то в стержнях расположенных на одной прямой усилия одинаковы.

Доказательство:

, и далее S₁ = S₂.