Результаты Вариант № 401

№ п/п	Номер	Тип	Правильный ответ
1	77333	B1	318,6
2	26876	B2	3
3	27677	B3	8
4	26679	B4	178200
5	282849	B5	3
6	27898	B6	2,5
7	26759	B7	2
8	27486	B8	-1
9	245367	B9	2
10	320185	B10	0,25
11	27072	B11	4
12	42519	B12	180000
13	99596	B13	20
14	500254	B14	1

↑ Задание 1 № 77333 тип B1 1 киловатт-час электроэнергии стоит 1 рубль 80 копеек. Счетчик электроэнергии 1 ноября показывал 12 625 киловатт-часов, а 1 декабря показывал 12 802 киловатт-часа. Сколько рублей нужно заплатить за электроэнергию за ноябрь? Решение. Расход электроэнергии за ноябрь составляет 12 802 − 12 625 = 177 киловатт-часов. Значит, за электроэнергию за ноябрь нужно заплатить 1,8   177 = 318,6 рубля.

Ответ: 318,6.

↑ Задание 2 № 26876 тип B2 На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 13 по 20 января. Ответ дайте в миллиметрах.

Решение. Из графика видно, что наибольшее количество осадков в период с 13 по 20 января выпало 14 января и составляло 3 мм (см. рисунок). Ответ: 3.

↑ Задание 3 № 27677 тип B3

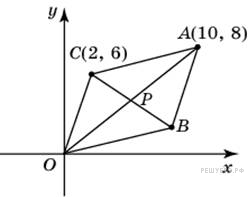Точки O(0; 0), A(10; 8), C(2; 6) и B являются вершинами параллелограмма. Найдите абсциссу точки B. Решение. Точка P является серединой отрезков OAи BC. Координаты точки P вычисляются следующим образом: , ,

но с другой стороны, , .

Поэтому , . Ответ: 8.

↑ Задание 4 № 26679 тип B4

Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.

Поставщик	Цена бруса (руб. за 1 м3)	Стоимость доставки	Дополнительные условия
A	4200	10200
Б	4800	8200	При заказе на сумму больше 150 000 руб. доставка бесплатно
В	4300	8200	При заказе на сумму больше 200 000 руб. доставка бесплатно

Решение. Рассмотрим все варианты. При покупке у поставщика A стоимость заказа складывается из стоимости бруса 4200   40 = 168 000 руб. и стоимости доставки: 168 000 + 10 200 = 178 200 руб. При покупке у поставщика Б стоимость бруса составляет 4800   40 = 192 000 руб., что превышает 150 000 руб., поэтому доставка бесплатна. Таким образом, стоимость заказа 192 000 руб. При покупке у поставщика В стоимость заказа складывается из стоимости бруса 4300   40 = 172 000 руб. и стоимости доставки: 172 000 + 8200 = 180 200 руб. Стоимость самого дешевого варианта составляет 178 200 рублей. Ответ: 178 200.

↑ Задание 5 № 282849 тип B5 Найдите корень уравнения . Решение. Извлекая кубический корень из обеих частей уравнения, получаем , откуда .

Правильный ответ: 3

↑ Задание 6 № 27898 тип B6

В треугольнике , , угол равен 90°. Найдите радиус описанной окружности этого треугольника. Решение. вписанный угол, опирающийся на диаметр окружности, является прямым, значит, – диаметр.

Ответ: 2,5.

↑ Задание 7 № 26759 тип B7 найдите значение выражения . Решение. Выполним преобразования: . Ответ: 2.

↑ Задание 8 № 27486 тип B8 Прямая является касательной к графику функции . Найдите абсциссу точки касания. Решение. Условие касания графика функции и прямой задаётся системой требований:

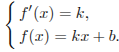
В нашем случае имеем:

Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания −1.

Ответ: −1.

↑ Задание 9 № 245367 тип B9

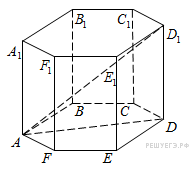В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла Решение. Рассмотрим прямоугольный треугольник катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне: . Поскольку имеем: Ответ: 2.

↑ Задание 10 № 320185 тип B10 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орёл, а во второй — решка. Решение. Всего возможных исходов — четыре: орел-орел, орел-решка, решка-орел, решка-решка. Благоприятным является один: орел-решка. Следовательно, искомая вероятность равна 1 : 4 = 0,25. Ответ: 0,25.

↑ Задание 11 № 27072 тип B11

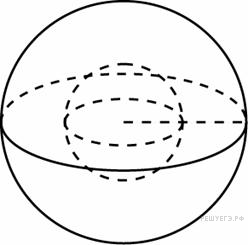Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? Решение. Площадь поверхности шара выражается через его радиус формулой , поэтому при увеличении радиуса вдвое площадь увеличится в 2² = 4 раза.

Ответ: 4.

↑ Задание 12 № 42519 тип B12

При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где  м — длина покоящейся ракеты,  км/с — скорость света, а  — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 68 м? Ответ выразите в км/с. Решение. Найдем, при какой скорости длина ракеты станет равна 68 м. Задача сводится к решению уравнения при заданном значении длины покоящейся ракеты м и известной величине скорости света км/с:

км/с.

Если скорость будет превосходить найденную, то длина ракеты будет менее 68 метров, поэтому минимальная необходимая скорость равна 180 000 км/с.

Ответ: 180 000.

↑ Задание 13 № 99596 тип B13 Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? Решение. Пусть км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна км/ч. Пусть первый раз мотоциклисты поравняются через часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому

. Таким образом, мотоциклисты поравняются через  часа или через 20 минут. Ответ: 20.

Приведём другое решение. Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.

↑ Задание 14 № 500254 тип B14 Найдите наибольшее значение функции на отрезке . Решение. Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

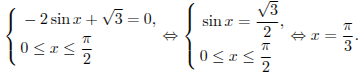
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

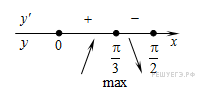
В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

. Ответ: 1.