
- •Результаты Вариант № 275
- •Результаты Вариант № 276
- •Результаты Вариант № 277
- •Задание 4 № 316049 тип b4
- •Задание с1 № 500131
- •Задание с2 № 500588
- •Задание с3 № 484579
- •Задание с4 № 485990
- •Задание с5 № 484630
- •Задание с6 № 500412
- •Результаты Вариант № 278
- •Результаты Вариант № 399
- •Решения
- •Проверка части с
- •Результаты Вариант № 400
- •Результаты Вариант № 401
- •Проверка части с
- •Результаты Вариант № 402
- •Результаты Вариант № 403
- •Результаты Вариант № 404
- •Проверка части с
- •Задание с1 № 484557
- •Задание с2 № 484560
- •Задание с3 № 500589
- •Задание с4 № 500876
- •Задание с5 № 484635
- •Задание с6 № 484662
- •Результаты Вариант № 405
- •Задание с1 № 484542
- •Задание с2 № 500193
- •Задание с3 № 484595
- •Задание с4 № 500015
- •Задание с5 № 500390
- •Задание с6 № 484657
- •Результаты Вариант № 406
- •Задание с1 № 485942
- •Задание с2 № 484562
- •Задание с4 № 500900
- •Задание с5 № 500350
- •Задание с6 № 484653
- •Вариант № 407
- •Задание с1 № 485996
- •Задание с2 № 484574
- •Задание с3 № 485951
- •Задание с4 № 485949
- •Задание с5 № 484644
- •Задание с6 № 500017
- •Вариант № 408
- •Задание с1 № 485973
- •Задание с2 № 484560
- •Задание с3 № 485969
- •Задание с4 № 500003
- •Задание с5 № 500471
- •Задание с6 № 484656
- •Вариант № 409
- •Задание с1 № 484553
- •Задание с2 № 500024
- •Задание с3 № 485944
- •Задание с4 № 484616
- •Задание с5 № 500016
- •Задание с6 № 500005
- •Вариант № 410
- •Задание с1 № 485977
- •Задание с2 № 486000
- •Задание с3 № 500020
- •Задание с4 № 485945
- •Задание с5 № 484642
- •Задание с6 № 500820
- •Результаты Вариант № 411
- •Задание с1 № 484550
- •Задание с2 № 484577
- •Задание с3 № 484604
- •Задание с4 № 500430
- •Задание с5 № 500196
- •Задание с6 № 484655
- •Результаты Вариант № 412
- •Задание с1 № 485964
- •Задание с2 № 500013
- •Задание с3 № 500368Решить систему неравенств
- •Задание с4 № 500369
- •Задание с5 № 484645
- •Задание с6 № 484666
- •Результаты Вариант № 413
- •Задание с1 № 500638 а) Решите уравнение . Б) Найдите все корни этого уравнения, принадлежащие промежутку .
- •Задание с2 № 500387
- •Задание с3 № 500449
- •Задание с4 № 500349
- •Задание с5 № 484648
- •Задание с6 № 500452
- •Вариант № 1939 447
- •Задание с1 № 484542
- •Задание с2 № 485981
- •Задание с3 № 484598
- •Задание с4 № 484615
- •Задание с5 № 500965
- •Задание с6 № 484655
- •Результаты Вариант № 14
- •Проверка части с
- •Результаты варианта 12
- •Результаты варианта 4 и 12
- •Проверка части с
- •Задание с1 № 500427
- •Задание с2 № 484571
- •Задание с3 № 500388
- •Задание с4 № 484610
- •Задание с5 № 484633
- •Задание с6 № 485960
- •Вариант № 1940591
- •Задание с1 № 485977
- •Задание с2 № 484559
- •Задание с3 № 500449
- •Задание с4 № 500410
- •Задание с5 № 484647
- •Задание с6 № 500966
- •Вариант № 1941093
- •Задание с1 № 500638
- •Задание с2 № 485955
- •Задание с3 № 500409
- •Задание с4 № 484613
- •Задание с5 № 484644
- •Задание с6 № 484654
- •Вариант № 1941368
- •Задание с1 № 484553 Решите уравнение .
- •Задание с2 № 484559
- •Задание с3 № 500368
- •Задание с4 № 500015
- •Задание с5 № 484633
- •Задание с6 № 484655
Результаты Вариант № 400
№ п/п |
Номер |
Тип |
Правильный ответ |
1 |
77333 |
B1 |
318,6 |
2 |
27516 |
B2 |
-2 |
3 |
27700 |
B3 |
3 |
4 |
246261 |
B4 |
3534 |
5 |
39007 |
B5 |
23 |
6 |
27398 |
B6 |
0,28 |
7 |
26828 |
B7 |
121 |
8 |
317542 |
B8 |
5 |
9 |
318474 |
B9 |
0,6 |
10 |
320198 |
B10 |
0,07 |
11 |
27132 |
B11 |
288 |
12 |
27954 |
B12 |
5000 |
13 |
99568 |
B13 |
27 |
14 |
77436 |
B14 |
-2 |
↑ Задание 1 № 77333 тип B1 1 киловатт-час электроэнергии стоит 1 рубль 80 копеек. Счетчик электроэнергии 1 ноября показывал 12 625 киловатт-часов, а 1 декабря показывал 12 802 киловатт-часа. Сколько рублей нужно заплатить за электроэнергию за ноябрь? Решение. Расход электроэнергии за ноябрь составляет 12 802 − 12 625 = 177 киловатт-часов. Значит, за электроэнергию за ноябрь нужно заплатить 1,8 177 = 318,6 рубля.
Ответ: 318,6.
Служба поддержки:
Поскольку требуется заплатить 318 рублей 60 копеек, а ответ нужно выразить в рублях, получаем 318,6 рубля. Если бы требовалось округлять, об этом было бы прямо сказано в условии. Но в условии указания округлять нет.
↑ Задание 2 № 27516 тип
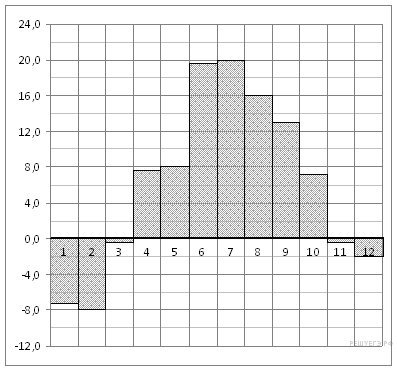
B2 На диаграмме
показана среднемесячная температура
воздуха в Санкт-Петербурге за каждый
месяц 1999 года. По горизонтали указываются
месяцы, по вертикали — температура
в градусах Цельсия. Определите по
диаграмме наименьшую среднемесячную
температуру во второй половине 1999 года.
Ответ дайте в градусах Цельсия.
Решение.
Из
диаграммы видно, что наименьшая
среднемесячная температура во второй
половине года составляла −2 °C (см.
рисунок).
Задание 2 № 27516 тип
B2 На диаграмме
показана среднемесячная температура
воздуха в Санкт-Петербурге за каждый
месяц 1999 года. По горизонтали указываются
месяцы, по вертикали — температура
в градусах Цельсия. Определите по
диаграмме наименьшую среднемесячную
температуру во второй половине 1999 года.
Ответ дайте в градусах Цельсия.
Решение.
Из
диаграммы видно, что наименьшая
среднемесячная температура во второй
половине года составляла −2 °C (см.
рисунок).
Ответ: −2.
↑ Задание 3 № 27700 тип B3
Н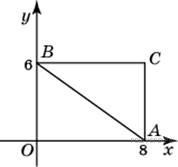 айдите
ординату центра окружности, описанной
около треугольника, вершины которого
имеют координаты (8; 0), (0; 6), (8; 6).
Решение.
айдите
ординату центра окружности, описанной
около треугольника, вершины которого
имеют координаты (8; 0), (0; 6), (8; 6).
Решение.
![]() ,
,
![]() ,
,
![]() .
.
Треугольник
является прямоугольным, так как
![]() .
Центр окружности, описанной около
прямоугольного треугольника, совпадает
с серединой гипотенузы.
Тогда можно
легко найти координаты центра окружности:
.
Центр окружности, описанной около
прямоугольного треугольника, совпадает
с серединой гипотенузы.
Тогда можно
легко найти координаты центра окружности:
![]() ,
,
![]() .
.
Ответ: 3.
↑ Задание 4 № 246261 тип B4 В среднем гражданин А. в дневное время расходует 125 кВт ч электроэнергии в месяц, а в ночное время — 155 кВт ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,6 руб. за кВт ч. Год назад А. установил двухтарифный счeтчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,6 руб. за кВт ч, а ночной расход оплачивается по тарифу 0,7 руб. за кВт ч. В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
Решение. Рассмотрим оба типа счётчиков. При использовании однотарифного счётчика, гражданин А. платил в месяц
(125 кВт ч + 155 кВт ч) 2,6 руб. за 1 кВт ч = 728 руб.
Поэтому за 12 месяцев он платил 728 1 2 = 8736 руб. При использовании двухтарифного счётчика, гражданин А. платит в месяц
125 кВт ч 2,6 руб. + 155 кВт ч 0,7 руб. = 433,5 руб.
Поэтому за 12 месяцев он заплатит 433,5 руб. 12 = 5202 руб. Установка нового типа счётчика позволяет экономить 8736 руб. − 5202 руб. = 3534 руб. в год.
Ваш ответ: нет ответа. Правильный ответ: 3534
↑
Задание 5 № 39007 тип
B5 Найдите
корень уравнения
![]() .
Решение.
Возведем
обе части уравнения в третью степень:
.
Решение.
Возведем
обе части уравнения в третью степень:
![]()
 Ответ:
23.
Ответ:
23.
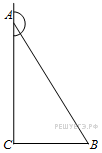
↑ Задание 6 № 27398 тип B6
В
треугольнике
угол
равен
90°, тангенс внешнего угла при вершине
равен
![]() .
Найдите
.
Найдите
![]() .
Решение.
так
как
.
Решение.
так
как
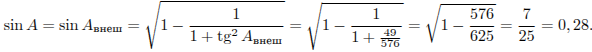
Ответ: 0,28.
↑
Задание 7 № 26828 тип
B7 Найдите
значение выражения
![]() при
при
![]() .
Решение.
Выполним преобразования:
.
Решение.
Выполним преобразования:
![]() .
Ответ:
121.
.
Ответ:
121.
 ↑
Задание 8 №
317542 тип B8
↑
Задание 8 №
317542 тип B8
На
рисунке изображён график
![]() производной
функции
и
восемь точек на оси абсцисс:
производной
функции
и
восемь точек на оси абсцисс:
![]()
![]()
![]() ,
,![]() .
В скольких из этих точек функция
убывает?
.
В скольких из этих точек функция
убывает?
Решение.
Убыванию
дифференцируемой функции
соответствуют
отрицательные значения её производной.
Производная отрицательна в точках
![]() Следовательно,
таких точек 5.
Следовательно,
таких точек 5.
Ответ:5.
↑ Задание 9 № 318474 тип B9
В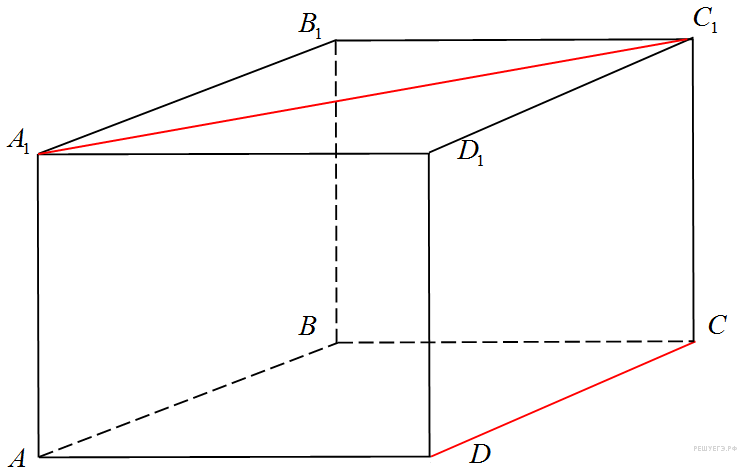 прямоугольном параллелепипеде
известны
длины рёбер
прямоугольном параллелепипеде
известны
длины рёбер
![]() ,
,
![]() ,
,
![]() .
Найдите синус угла между прямыми
и
.
Найдите синус угла между прямыми
и
![]() .
Решение.
Отрезки
DC
и D1C1
лежат на параллельных прямых, поэтому
искомый угол между прямыми A1C1
и DC
равен углу между прямыми A1C1
и D1C1.
Из прямоугольного треугольника
A1C1D1
по получаем:
.
Решение.
Отрезки
DC
и D1C1
лежат на параллельных прямых, поэтому
искомый угол между прямыми A1C1
и DC
равен углу между прямыми A1C1
и D1C1.
Из прямоугольного треугольника
A1C1D1
по получаем:
![]()
Тогда для угла A1C1D1 имеем:
![]() Ответ:0,6.
Ответ:0,6.
↑ Задание 10 № 320198 тип B10
Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. Решение. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
Ответ: 0,07.
↑ Задание 11 № 27132
тип B11
Задание 11 № 27132
тип B11
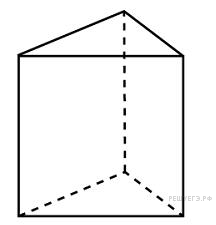
Основанием
прямой треугольной призмы служит
прямоугольный треугольник с катетами
6 и 8, высота призмы равна 10. Найдите
площадь ее поверхности.
Решение.
Третья
сторона треугольника в основании равна
10 и его площадь
![]() Площадь
боковой поверхности призмы с периметром
основания
равна
Площадь
боковой поверхности призмы с периметром
основания
равна
![]() .
.
Полная
площадь поверхности:
![]() Ответ:
288.
Ответ:
288.
↑ Задание 12 № 27954 тип B12
Некоторая
компания продает свою продукцию по цене
![]() руб.
за единицу, переменные затраты на
производство одной единицы продукции
составляют
руб.
за единицу, переменные затраты на
производство одной единицы продукции
составляют
![]() руб.,
постоянные расходы предприятия
руб.,
постоянные расходы предприятия
![]() руб.
месяц. Месячная операционная прибыль
предприятия (в рублях) вычисляется по
формуле
руб.
месяц. Месячная операционная прибыль
предприятия (в рублях) вычисляется по
формуле
![]() .
Определите наименьший месячный объeм
производства
(единиц
продукции), при котором месячная
операционная прибыль предприятия будет
не меньше 300000 руб.
Решение.
Задача
сводится к нахождению наименьшего
решения неравенства
.
Определите наименьший месячный объeм
производства
(единиц
продукции), при котором месячная
операционная прибыль предприятия будет
не меньше 300000 руб.
Решение.
Задача
сводится к нахождению наименьшего
решения неравенства
![]() руб.
при заданных значениях цены за единицу
руб.,
переменных затрат на производство одной
единицы продукции
руб.
и постоянных расходов предприятия
руб.
при заданных значениях цены за единицу
руб.,
переменных затрат на производство одной
единицы продукции
руб.
и постоянных расходов предприятия
![]()
![]() руб.
в месяц:
руб.
в месяц:
![]()
![]() Ответ:
5000.
Ответ:
5000.
↑ Задание 13 № 99568 тип B13
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены? Решение. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%, то есть зарплата мужа составляет 67% дохода семьи. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%, то есть 2/3 стипендии составляют 4% дохода семьи, а вся стипендия дочери составляет 6% дохода семьи. Таким образом, доход жены составляет 100% − 67% − 6% = 27% дохода семьи. Ответ: 27.
↑
Задание 14 № 77436
тип B14
Найдите точку минимума функции
![]() .
Решение.
Найдем производную заданной функции:
.
Решение.
Найдем производную заданной функции:
![]() Найдем нули
производной:
Найдем нули
производной:
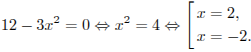
Определим знаки производной функции и изобразим на рисунке поведение функции:
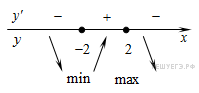 Искомая
точка минимума
Искомая
точка минимума
![]() .
.
Ответ: −2.
Начало формы
Задание С1 № 484554
Решите
уравнение
![]() .
.
Решение.
Уравнение равносильно системе
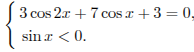
Уравнение
системы приводится к виду
![]() ,
откуда
или
,
откуда
или
![]() .
Уравнение
не имеет решений. Учитывая, что
.
Уравнение
не имеет решений. Учитывая, что
![]() ,
получаем:
,
получаем:
![]() .
Ответ:
.
.
Ответ:
.
Задание С2 № 484568 Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка M — середина бокового ребра пирамиды AP.
Р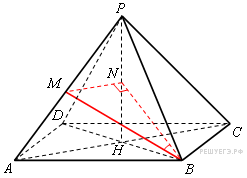 ешение.
ешение.
Пусть
отрезок PH —
высота пирамиды PABCD,
отрезок MN —
средняя линия треугольника APH
(см. рисунок).
Поскольку PABCD —
правильная пирамида, точка H —
центр квадрата ABCD,
значит,
![]() и
и
![]() ,
откуда
,
откуда
![]() .
Но,
.
Но,
![]() ,
следовательно,
,
следовательно,
![]() .
Таким образом, прямая BN —
проекция прямой BM
на плоскость BDP,
значит, угол мужду прямой BM
и плоскостью BDP
равен углу между прямой BM
и прямой BN,
т. е. острому углу MBN
прямоугольного треугольника MBN.
.
Таким образом, прямая BN —
проекция прямой BM
на плоскость BDP,
значит, угол мужду прямой BM
и плоскостью BDP
равен углу между прямой BM
и прямой BN,
т. е. острому углу MBN
прямоугольного треугольника MBN.
Примем
длину ребра данной пирамиды за 1, тогда
![]() ,
,
![]() ,
,
![]() и,
следовательно,
и,
следовательно,
![]() ,
,
![]() .
Ответ:
.
.
Ответ:
.
Задание С3 № 485969
Решите систему
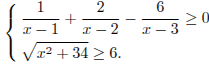
Решение.
Решим первое неравенство
![]()
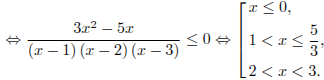
2.
Решим второе неравенство:
![]() .
Значит,
.
Значит,
![]() или
или
![]() 3.
Решением системы является общая часть
решений двух неравенств. Поскольку
3.
Решением системы является общая часть
решений двух неравенств. Поскольку
![]() ,
получаем:
,
получаем:
,
![]() или
или
![]() .
.
Ответ: , , .
Задание С4 № 484616 Окружность S проходит через вершину C прямого угла и пресекает его стороны в точках, удаленных от вершины C на расстояния 6 и 8. Найдите радиус окружности, вписанной в данный угол и касающийся окружности S.
Решение.
Пусть
окружность S
с центром O
и радиусом R
пересекает стороны данного прямого
угла в точках A
и B,
![]() ,
искомая окружность с центром Q
касается сторон и BC
угла ACB
в точках N
и K
соответственно, а окружности S —
в точке M.
,
искомая окружность с центром Q
касается сторон и BC
угла ACB
в точках N
и K
соответственно, а окружности S —
в точке M.
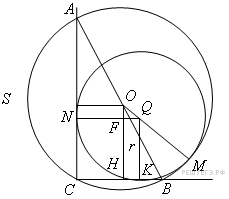
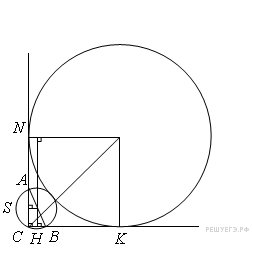
Точка O — центр окружности, описанной около прямоугольного треугольника ABC, поэтому O — середина его гипотенузы AB.
![]() .
.
Линия
центров двух касающихся окружностей
проходит через точку их касания, поэтому
точки M,
O
и Q
лежат на одной прямой. Опустим перпендикуляр
OH
из центра окружности S
на прямую BC.
Тогда OH —
средняя линия треугольника ABC
поэтому
![]() и
и
![]() ,
а т.к. центр окружности, вписанной в
угол, лежит на его биссектрисе, то
,
а т.к. центр окружности, вписанной в
угол, лежит на его биссектрисе, то
![]() ,
поэтому
,
поэтому
![]() .
Опустим перпендикуляр QF
из центра искомой окружности на прямую
OH.
Тогда
.
Опустим перпендикуляр QF
из центра искомой окружности на прямую
OH.
Тогда
![]() .
.
Предположим, что искомая окружность и окружность касаются внутренним образом. Тогда
![]() .
.
Рассмотрим
прямоугольный треугольник OFQ.
По теореме Пифагора
![]() или
или
![]() откуда
находим, что
откуда
находим, что
![]() .
.
Если же искомая окружность касается данной внешним образом, то
![]() .
.
Тогда
из соответствующего уравнения
![]() находим,
что
находим,
что
![]() .
Ответ: 4 или 24.
.
Ответ: 4 или 24.
Задание С5 № 500431
Найдите
все значения a , при каждом из которых
уравнение
![]() либо
имеет единственное решение, либо не
имеет решений.
либо
имеет единственное решение, либо не
имеет решений.
Решение.
Введём
обозначения:
![]() ,
,
![]() ,
,
![]() .
В этих обозначениях исходное уравнение
принимает вид
.
В этих обозначениях исходное уравнение
принимает вид
![]() .
Заметим, что
.
Заметим, что
![]() при
при
![]() ,
,
![]() при
при
![]() .
Покажем, что при
.
Покажем, что при
![]() уравнение
либо
имеет единственное решение, либо не
имеет решений.
Действительно,
если
,
то
уравнение
либо
имеет единственное решение, либо не
имеет решений.
Действительно,
если
,
то
![]() .
Если
,
то
.
Если
,
то
![]()
причём
равенство достигается только при
![]() и
.
При
и
.
При
![]() верны
неравенства
верны
неравенства
![]() и
и
![]() ,
так как
,
так как
![]() и
и
![]() .
Значит, уравнение
имеет
решение.
Если некоторое число
.
Значит, уравнение
имеет
решение.
Если некоторое число
![]() является
решением этого уравнения, то и число
является
решением этого уравнения, то и число
![]() также
является его решением, поскольку функции
и
также
является его решением, поскольку функции
и
![]() —
чётные. Значит, если уравнение f ( x ) = g (
x ) имеет единственное решение, то это
решение
.
Решим уравнение
—
чётные. Значит, если уравнение f ( x ) = g (
x ) имеет единственное решение, то это
решение
.
Решим уравнение
![]() относительно
относительно
![]() :
:
![]()
значит,
является
решением уравнения
при
![]() или
.
Случай, когда |b| = 2, уже был разобран.
При
уравнение
принимает вид
или
.
Случай, когда |b| = 2, уже был разобран.
При
уравнение
принимает вид
![]() и
имеет три различных решения:
и
имеет три различных решения:![]() ,
,
,
,
![]() .
Таким образом, уравнение
имеет
единственное решение или не имеет
решений при
.
Таким образом, уравнение
имеет
единственное решение или не имеет
решений при
![]() и
и
![]() ,
то есть при
,
то есть при
![]() и
и
![]() .
Ответ:
;
.
.
Ответ:
;
.
Задание С6 № 484653 Среди обыкновенных дробей с положительными знаменателями, расположенных между числами и , найдите такую, знаменатель которой минимален. Решение.
Так как
и , то достаточно найти правильную дробь с наименьшим знаменателем, лежащую между числами
и , а затем прибавить к ней число 2. Среди дробей со знаменателями 2, 3, 4, 5 и 6 нужных дробей нет, так как
, , , , , , , .
Для знаменателя 7 получаем , т. е. . Ответ: .
